COMPARE: Clinical Optimization with Modular Planning and Assessment via RAG-Enhanced AI-OCT: Superior Decision Support for Percutaneous Coronary Intervention Compared to ChatGPT-5 and Junior Operators

Background: While intravascular imaging, particularly optical coherence tomography (OCT), improves percutaneous coronary intervention (PCI) outcomes, its interpretation is operator-dependent. General-purpose artificial intelligence (AI) shows promise but lacks domain-specific reliability. We evaluated the performance of CA-GPT, a novel large model deployed on an AI-OCT system, against that of the general-purpose ChatGPT-5 and junior physicians for OCT-guided PCI planning and assessment. Methods: In this single-center analysis of 96 patients who underwent OCT-guided PCI, the procedural decisions generated by the CA-GPT, ChatGPT-5, and junior physicians were compared with an expert-derived procedural record. Agreement was assessed using ten pre-specified metrics across pre-PCI and post-PCI phases. Results: For pre-PCI planning, CA-GPT demonstrated significantly higher median agreement scores (5[IQR 3.75-5]) compared to both ChatGPT-5 (3[2-4], P<0.001) and junior physicians (4[3-4], P<0.001). CA-GPT significantly outperformed ChatGPT-5 across all individual pre-PCI metrics and showed superior performance to junior physicians in stent diameter (90.3% vs. 72.2%, P<0.05) and length selection (80.6% vs. 52.8%, P<0.01). In post-PCI assessment, CA-GPT maintained excellent overall agreement (5[4.75-5]), significantly higher than both ChatGPT-5 (4[4-5], P<0.001) and junior physicians (5[4-5], P<0.05). Subgroup analysis confirmed CA-GPT's robust performance advantage in complex scenarios. Conclusion: The CA-GPT-based AI-OCT system achieved superior decision-making agreement versus a general-purpose large language model and junior physicians across both PCI planning and assessment phases. This approach provides a standardized and reliable method for intravascular imaging interpretation, demonstrating significant potential to augment operator expertise and optimize OCT-guided PCI.

Robust subspace clustering by Cauchy loss function

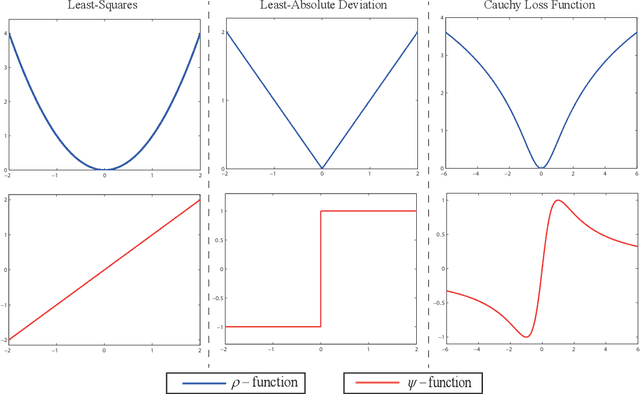
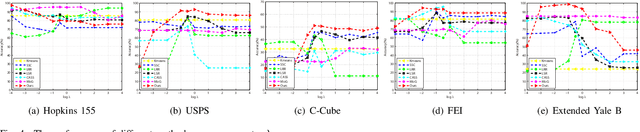
Subspace clustering is a problem of exploring the low-dimensional subspaces of high-dimensional data. State-of-the-arts approaches are designed by following the model of spectral clustering based method. These methods pay much attention to learn the representation matrix to construct a suitable similarity matrix and overlook the influence of the noise term on subspace clustering. However, the real data are always contaminated by the noise and the noise usually has a complicated statistical distribution. To alleviate this problem, we in this paper propose a subspace clustering method based on Cauchy loss function (CLF). Particularly, it uses CLF to penalize the noise term for suppressing the large noise mixed in the real data. This is due to that the CLF's influence function has a upper bound which can alleviate the influence of a single sample, especially the sample with a large noise, on estimating the residuals. Furthermore, we theoretically prove the grouping effect of our proposed method, which means that highly correlated data can be grouped together. Finally, experimental results on five real datasets reveal that our proposed method outperforms several representative clustering methods.

SCE: A manifold regularized set-covering method for data partitioning

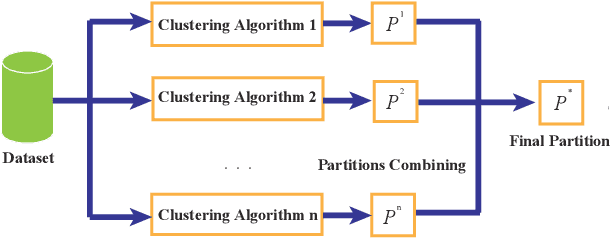
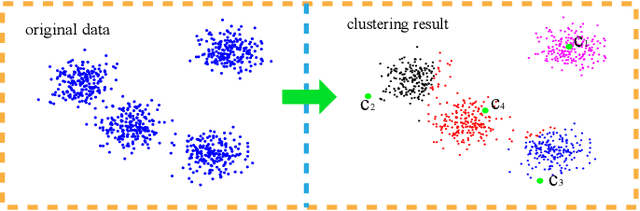
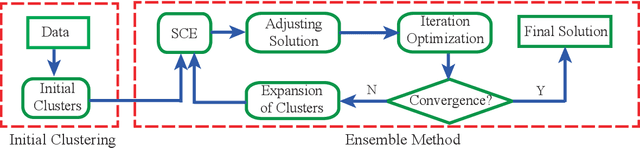
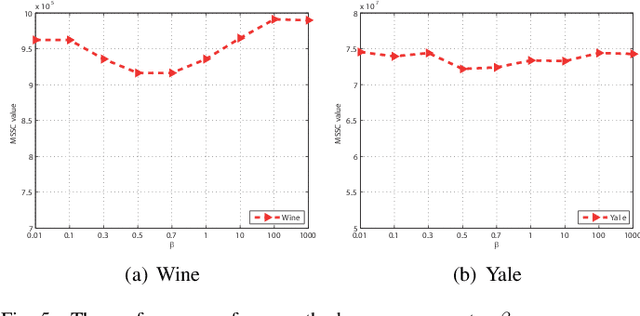
Cluster analysis plays a very important role in data analysis. In these years, cluster ensemble, as a cluster analysis tool, has drawn much attention for its robustness, stability, and accuracy. Many efforts have been done to combine different initial clustering results into a single clustering solution with better performance. However, they neglect the structure information of the raw data in performing the cluster ensemble. In this paper, we propose a Structural Cluster Ensemble (SCE) algorithm for data partitioning formulated as a set-covering problem. In particular, we construct a Laplacian regularized objective function to capture the structure information among clusters. Moreover, considering the importance of the discriminative information underlying in the initial clustering results, we add a discriminative constraint into our proposed objective function. Finally, we verify the performance of the SCE algorithm on both synthetic and real data sets. The experimental results show the effectiveness of our proposed method SCE algorithm.