Beyond Theorem Proving: Formulation, Framework and Benchmark for Formal Problem-Solving

As a seemingly self-explanatory task, problem-solving has been a significant component of science and engineering. However, a general yet concrete formulation of problem-solving itself is missing. With the recent development of AI-based problem-solving agents, the demand for process-level verifiability is rapidly increasing yet underexplored. To fill these gaps, we present a principled formulation of problem-solving as a deterministic Markov decision process; a novel framework, FPS (Formal Problem-Solving), which utilizes existing FTP (formal theorem proving) environments to perform process-verified problem-solving; and D-FPS (Deductive FPS), decoupling solving and answer verification for better human-alignment. The expressiveness, soundness and completeness of the frameworks are proven. We construct three benchmarks on problem-solving: FormalMath500, a formalization of a subset of the MATH500 benchmark; MiniF2F-Solving and PutnamBench-Solving, adaptations of FTP benchmarks MiniF2F and PutnamBench. For faithful, interpretable, and human-aligned evaluation, we propose RPE (Restricted Propositional Equivalence), a symbolic approach to determine the correctness of answers by formal verification. We evaluate four prevalent FTP models and two prompting methods as baselines, solving at most 23.77% of FormalMath500, 27.47% of MiniF2F-Solving, and 0.31% of PutnamBench-Solving.

Multi-View Graph Representation for Programming Language Processing: An Investigation into Algorithm Detection

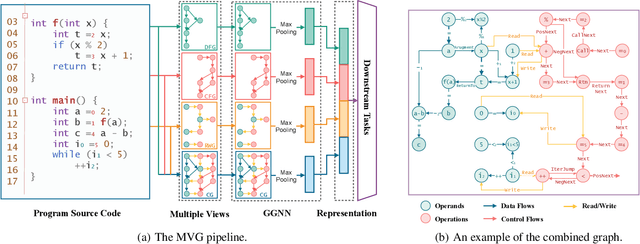
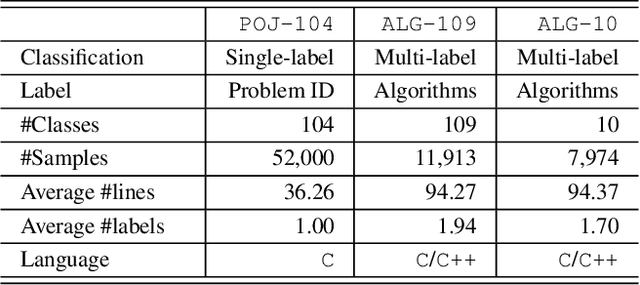
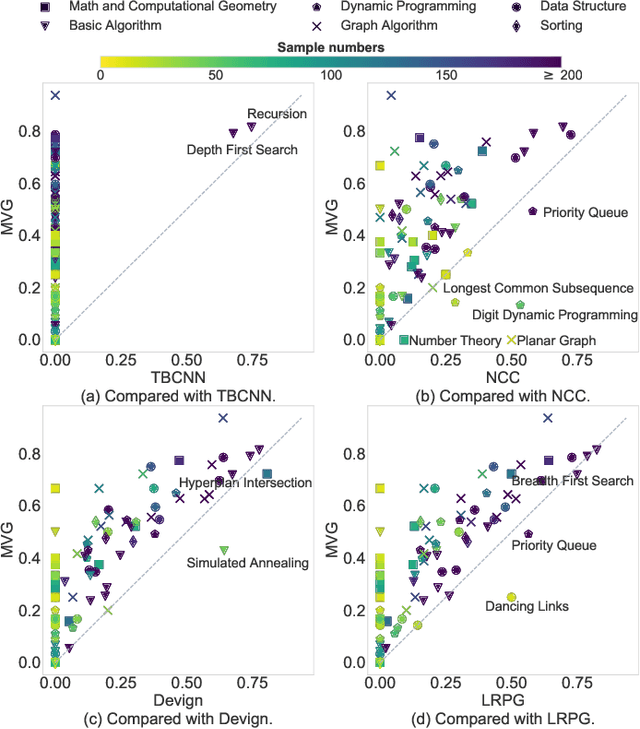
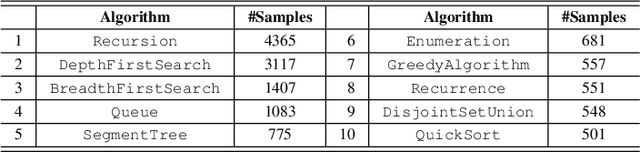
Program representation, which aims at converting program source code into vectors with automatically extracted features, is a fundamental problem in programming language processing (PLP). Recent work tries to represent programs with neural networks based on source code structures. However, such methods often focus on the syntax and consider only one single perspective of programs, limiting the representation power of models. This paper proposes a multi-view graph (MVG) program representation method. MVG pays more attention to code semantics and simultaneously includes both data flow and control flow as multiple views. These views are then combined and processed by a graph neural network (GNN) to obtain a comprehensive program representation that covers various aspects. We thoroughly evaluate our proposed MVG approach in the context of algorithm detection, an important and challenging subfield of PLP. Specifically, we use a public dataset POJ-104 and also construct a new challenging dataset ALG-109 to test our method. In experiments, MVG outperforms previous methods significantly, demonstrating our model's strong capability of representing source code.