Detecting Changes Between Optical Images of Different Spatial and Spectral Resolutions: a Fusion-Based Approach

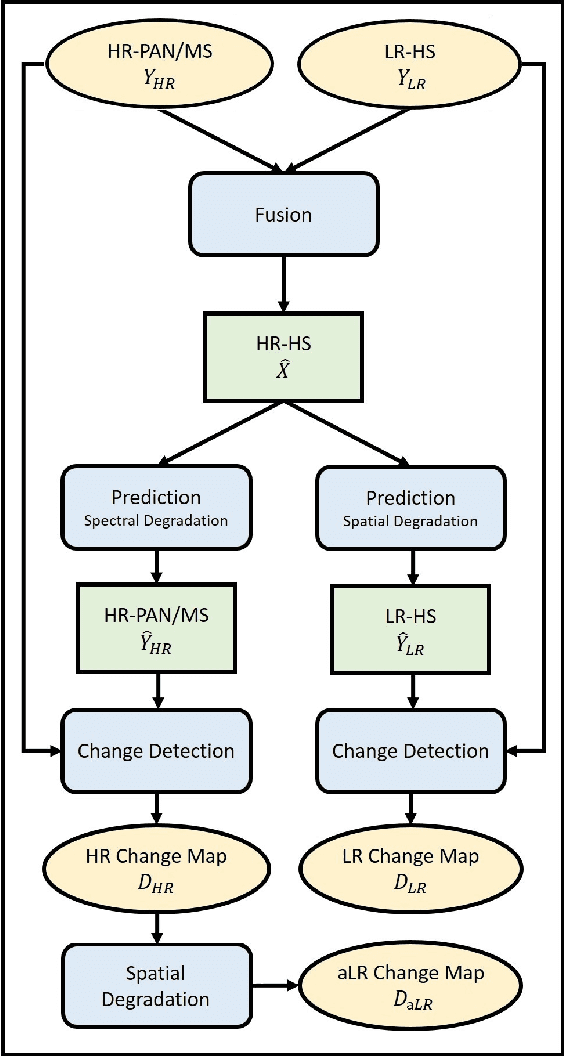
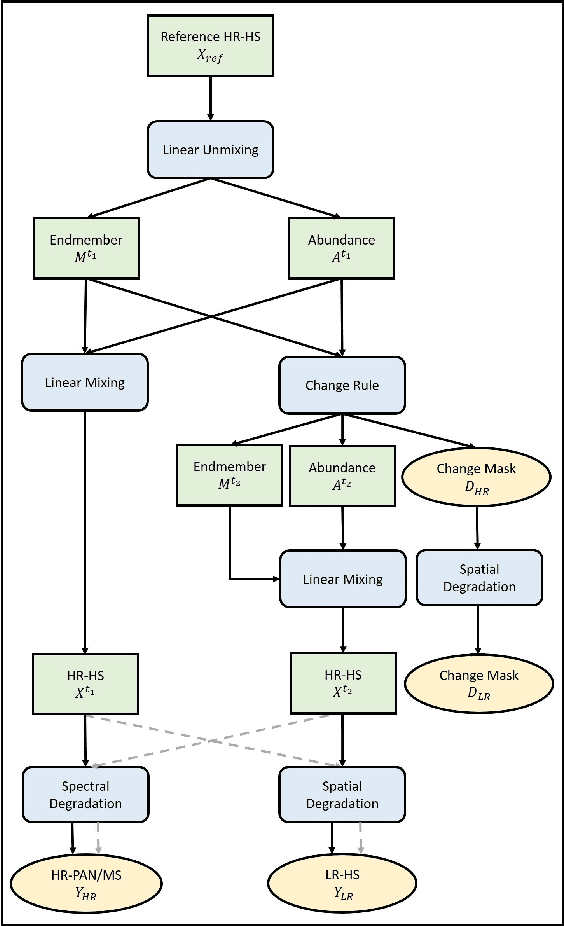
Change detection is one of the most challenging issues when analyzing remotely sensed images. Comparing several multi-date images acquired through the same kind of sensor is the most common scenario. Conversely, designing robust, flexible and scalable algorithms for change detection becomes even more challenging when the images have been acquired by two different kinds of sensors. This situation arises in case of emergency under critical constraints. This paper presents, to the best of authors' knowledge, the first strategy to deal with optical images characterized by dissimilar spatial and spectral resolutions. Typical considered scenarios include change detection between panchromatic or multispectral and hyperspectral images. The proposed strategy consists of a 3-step procedure: i) inferring a high spatial and spectral resolution image by fusion of the two observed images characterized one by a low spatial resolution and the other by a low spectral resolution, ii) predicting two images with respectively the same spatial and spectral resolutions as the observed images by degradation of the fused one and iii) implementing a decision rule to each pair of observed and predicted images characterized by the same spatial and spectral resolutions to identify changes. The performance of the proposed framework is evaluated on real images with simulated realistic changes.

Fast Single Image Super-Resolution

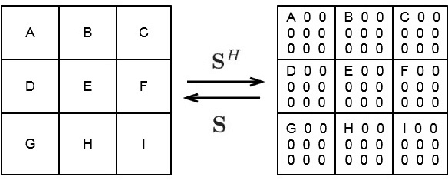
This paper addresses the problem of single image super-resolution (SR), which consists of recovering a high resolution image from its blurred, decimated and noisy version. The existing algorithms for single image SR use different strategies to handle the decimation and blurring operators. In addition to the traditional first-order gradient methods, recent techniques investigate splitting-based methods dividing the SR problem into up-sampling and deconvolution steps that can be easily solved. Instead of following this splitting strategy, we propose to deal with the decimation and blurring operators simultaneously by taking advantage of their particular properties in the frequency domain, leading to a new fast SR approach. Specifically, an analytical solution can be obtained and implemented efficiently for the Gaussian prior or any other regularization that can be formulated into an $\ell_2$-regularized quadratic model, i.e., an $\ell_2$-$\ell_2$ optimization problem. Furthermore, the flexibility of the proposed SR scheme is shown through the use of various priors/regularizations, ranging from generic image priors to learning-based approaches. In the case of non-Gaussian priors, we show how the analytical solution derived from the Gaussian case can be embedded intotraditional splitting frameworks, allowing the computation cost of existing algorithms to be decreased significantly. Simulation results conducted on several images with different priors illustrate the effectiveness of our fast SR approach compared with the existing techniques.

Unsupervised Nonlinear Spectral Unmixing based on a Multilinear Mixing Model

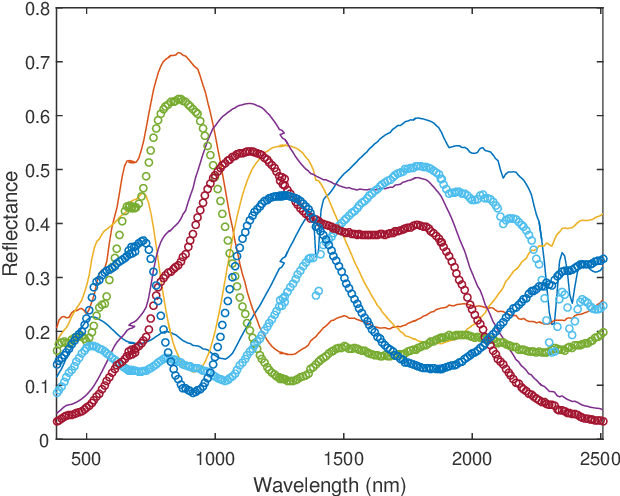
In the community of remote sensing, nonlinear mixing models have recently received particular attention in hyperspectral image processing. In this paper, we present a novel nonlinear spectral unmixing method following the recent multilinear mixing model of [1], which includes an infinite number of terms related to interactions between different endmembers. The proposed unmixing method is unsupervised in the sense that the endmembers are estimated jointly with the abundances and other parameters of interest, i.e., the transition probability of undergoing further interactions. Non-negativity and sum-to one constraints are imposed on abundances while only nonnegativity is considered for endmembers. The resulting unmixing problem is formulated as a constrained nonlinear optimization problem, which is solved by a block coordinate descent strategy, consisting of updating the endmembers, abundances and transition probability iteratively. The proposed method is evaluated and compared with linear unmixing methods for synthetic and real hyperspectral datasets acquired by the AVIRIS sensor. The advantage of using non-linear unmixing as opposed to linear unmixing is clearly shown in these examples.

R-FUSE: Robust Fast Fusion of Multi-Band Images Based on Solving a Sylvester Equation

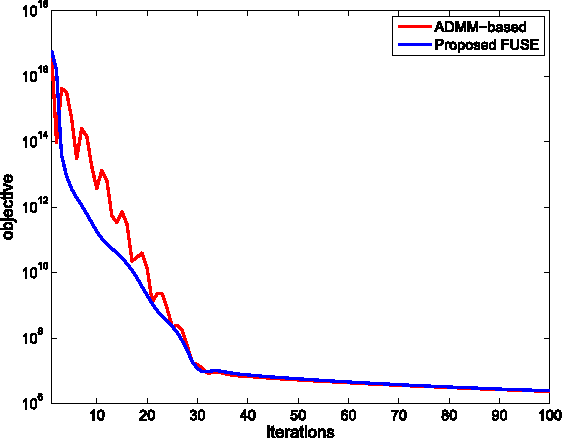
This paper proposes a robust fast multi-band image fusion method to merge a high-spatial low-spectral resolution image and a low-spatial high-spectral resolution image. Following the method recently developed in [1], the generalized Sylvester matrix equation associated with the multi-band image fusion problem is solved in a more robust and efficient way by exploiting the Woodbury formula, avoiding any permutation operation in the frequency domain as well as the blurring kernel invertibility assumption required in [1]. Thanks to this improvement, the proposed algorithm requires fewer computational operations and is also more robust with respect to the blurring kernel compared with the one in [1]. The proposed new algorithm is tested with different priors considered in [1]. Our conclusion is that the proposed fusion algorithm is more robust than the one in [1] with a reduced computational cost.

Multi-Band Image Fusion Based on Spectral Unmixing

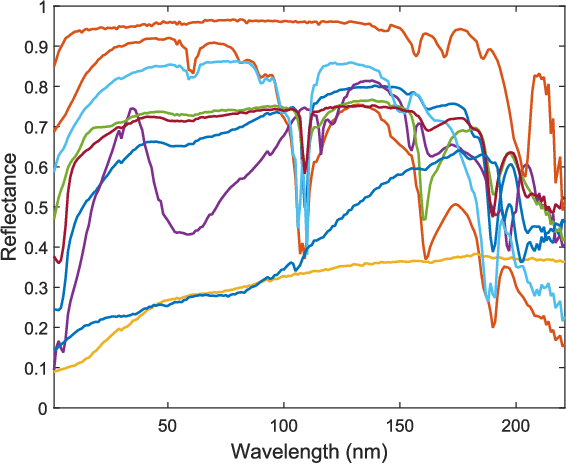
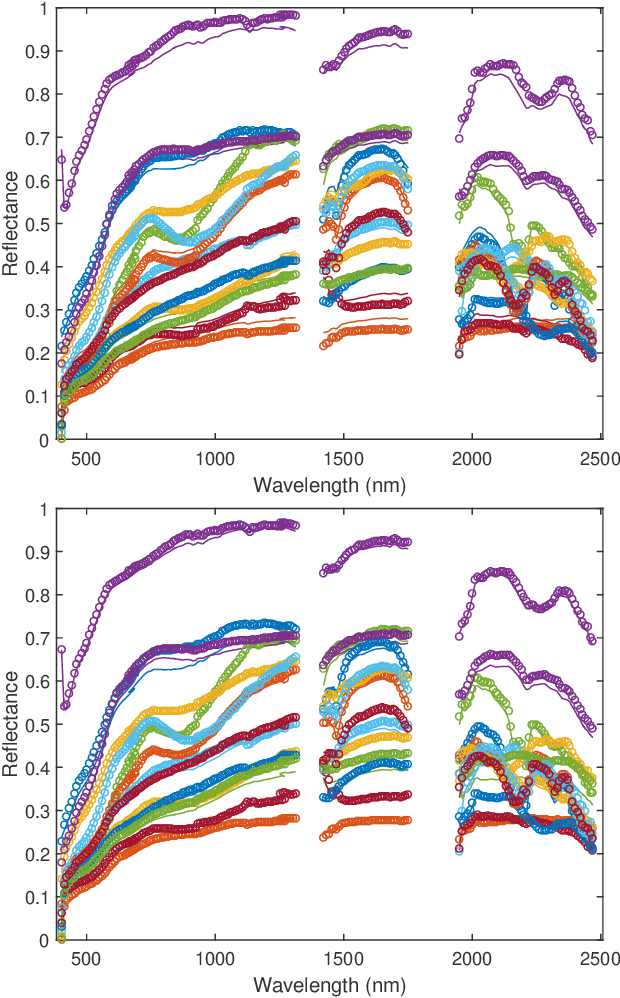
This paper presents a multi-band image fusion algorithm based on unsupervised spectral unmixing for combining a high-spatial low-spectral resolution image and a low-spatial high-spectral resolution image. The widely used linear observation model (with additive Gaussian noise) is combined with the linear spectral mixture model to form the likelihoods of the observations. The non-negativity and sum-to-one constraints resulting from the intrinsic physical properties of the abundances are introduced as prior information to regularize this ill-posed problem. The joint fusion and unmixing problem is then formulated as maximizing the joint posterior distribution with respect to the endmember signatures and abundance maps, This optimization problem is attacked with an alternating optimization strategy. The two resulting sub-problems are convex and are solved efficiently using the alternating direction method of multipliers. Experiments are conducted for both synthetic and semi-real data. Simulation results show that the proposed unmixing based fusion scheme improves both the abundance and endmember estimation comparing with the state-of-the-art joint fusion and unmixing algorithms.

Fast Spectral Unmixing based on Dykstra's Alternating Projection

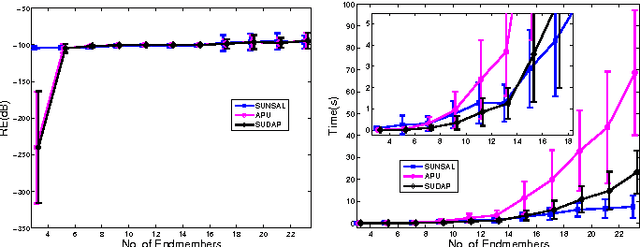
This paper presents a fast spectral unmixing algorithm based on Dykstra's alternating projection. The proposed algorithm formulates the fully constrained least squares optimization problem associated with the spectral unmixing task as an unconstrained regression problem followed by a projection onto the intersection of several closed convex sets. This projection is achieved by iteratively projecting onto each of the convex sets individually, following Dyktra's scheme. The sequence thus obtained is guaranteed to converge to the sought projection. Thanks to the preliminary matrix decomposition and variable substitution, the projection is implemented intrinsically in a subspace, whose dimension is very often much lower than the number of bands. A benefit of this strategy is that the order of the computational complexity for each projection is decreased from quadratic to linear time. Numerical experiments considering diverse spectral unmixing scenarios provide evidence that the proposed algorithm competes with the state-of-the-art, namely when the number of endmembers is relatively small, a circumstance often observed in real hyperspectral applications.

Hyperspectral pansharpening: a review

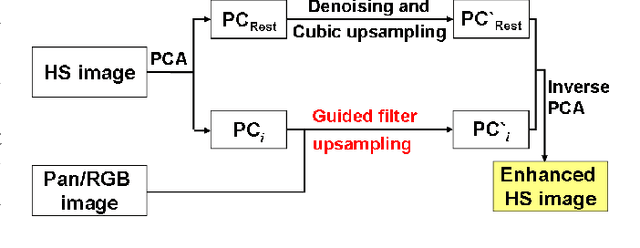
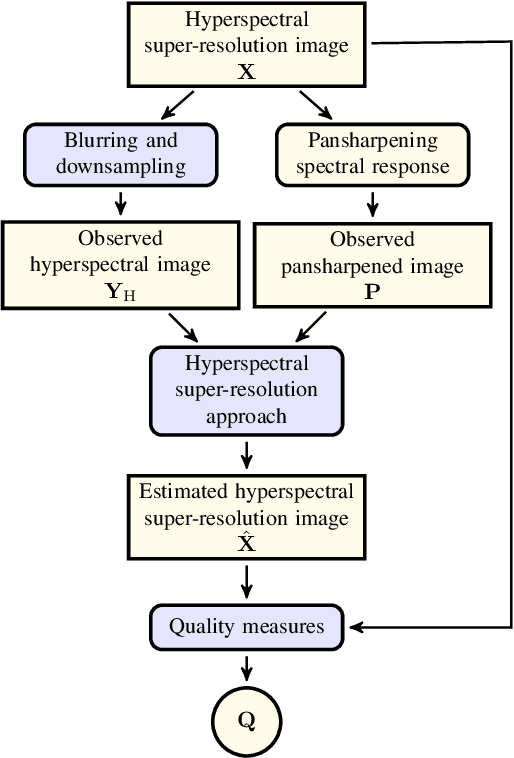
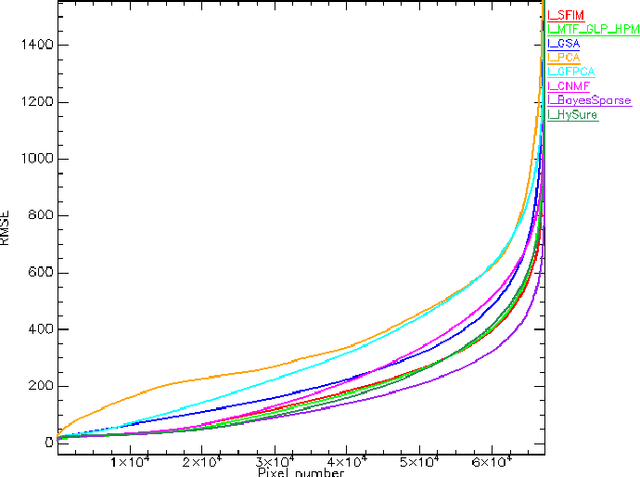
Pansharpening aims at fusing a panchromatic image with a multispectral one, to generate an image with the high spatial resolution of the former and the high spectral resolution of the latter. In the last decade, many algorithms have been presented in the literature for pansharpening using multispectral data. With the increasing availability of hyperspectral systems, these methods are now being adapted to hyperspectral images. In this work, we compare new pansharpening techniques designed for hyperspectral data with some of the state of the art methods for multispectral pansharpening, which have been adapted for hyperspectral data. Eleven methods from different classes (component substitution, multiresolution analysis, hybrid, Bayesian and matrix factorization) are analyzed. These methods are applied to three datasets and their effectiveness and robustness are evaluated with widely used performance indicators. In addition, all the pansharpening techniques considered in this paper have been implemented in a MATLAB toolbox that is made available to the community.

Fast Fusion of Multi-Band Images Based on Solving a Sylvester Equation

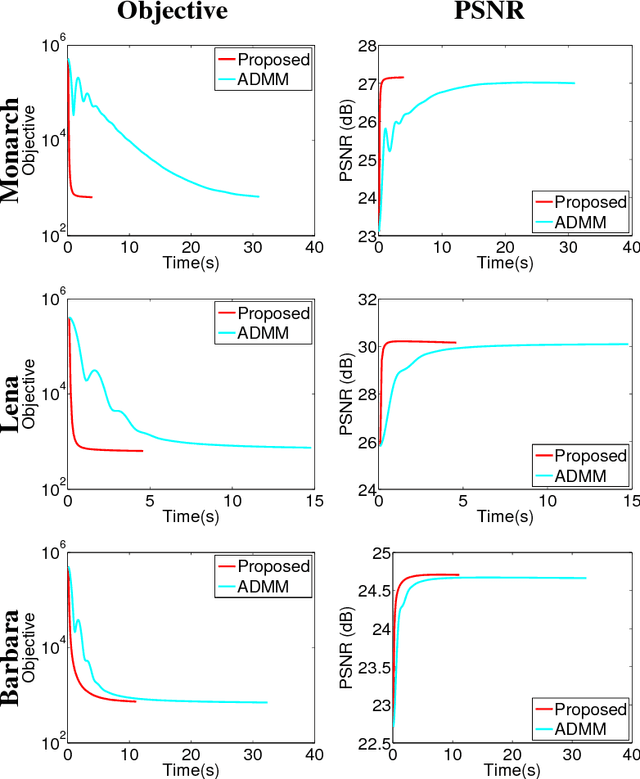
This paper proposes a fast multi-band image fusion algorithm, which combines a high-spatial low-spectral resolution image and a low-spatial high-spectral resolution image. The well admitted forward model is explored to form the likelihoods of the observations. Maximizing the likelihoods leads to solving a Sylvester equation. By exploiting the properties of the circulant and downsampling matrices associated with the fusion problem, a closed-form solution for the corresponding Sylvester equation is obtained explicitly, getting rid of any iterative update step. Coupled with the alternating direction method of multipliers and the block coordinate descent method, the proposed algorithm can be easily generalized to incorporate prior information for the fusion problem, allowing a Bayesian estimator. Simulation results show that the proposed algorithm achieves the same performance as existing algorithms with the advantage of significantly decreasing the computational complexity of these algorithms.

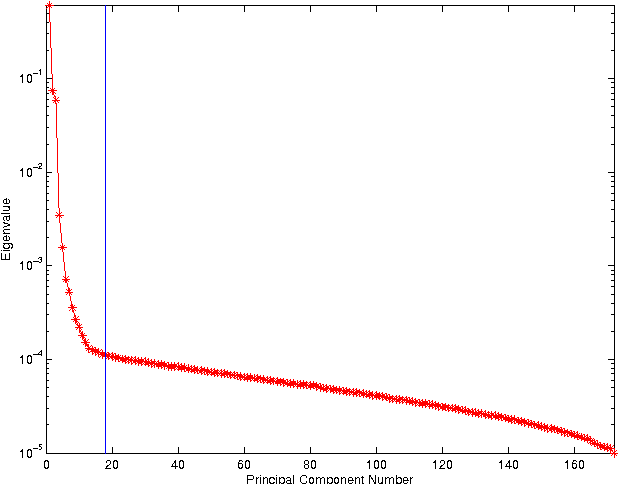
Hyperspectral and Multispectral Image Fusion based on a Sparse Representation

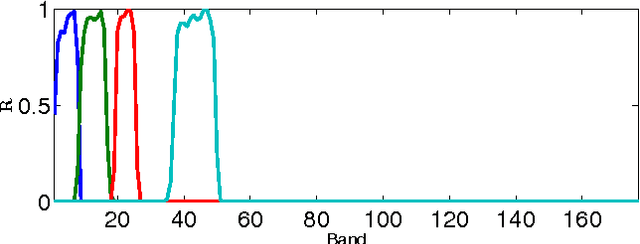
This paper presents a variational based approach to fusing hyperspectral and multispectral images. The fusion process is formulated as an inverse problem whose solution is the target image assumed to live in a much lower dimensional subspace. A sparse regularization term is carefully designed, relying on a decomposition of the scene on a set of dictionaries. The dictionary atoms and the corresponding supports of active coding coefficients are learned from the observed images. Then, conditionally on these dictionaries and supports, the fusion problem is solved via alternating optimization with respect to the target image (using the alternating direction method of multipliers) and the coding coefficients. Simulation results demonstrate the efficiency of the proposed algorithm when compared with the state-of-the-art fusion methods.

Bayesian Fusion of Multi-Band Images

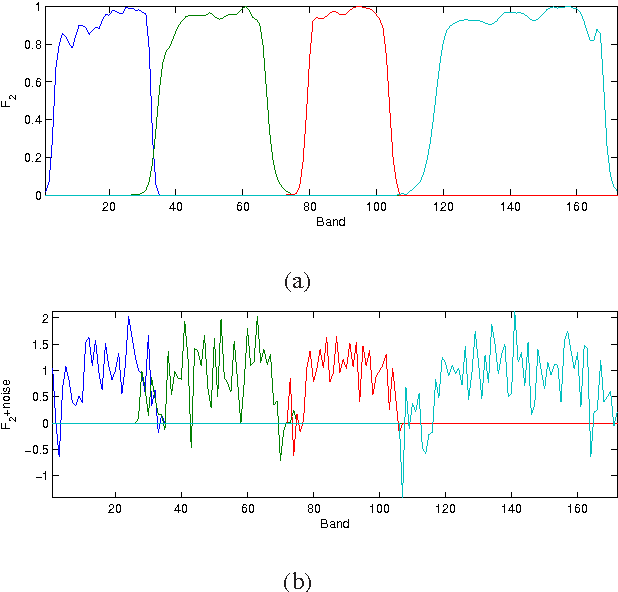
In this paper, a Bayesian fusion technique for remotely sensed multi-band images is presented. The observed images are related to the high spectral and high spatial resolution image to be recovered through physical degradations, e.g., spatial and spectral blurring and/or subsampling defined by the sensor characteristics. The fusion problem is formulated within a Bayesian estimation framework. An appropriate prior distribution exploiting geometrical consideration is introduced. To compute the Bayesian estimator of the scene of interest from its posterior distribution, a Markov chain Monte Carlo algorithm is designed to generate samples asymptotically distributed according to the target distribution. To efficiently sample from this high-dimension distribution, a Hamiltonian Monte Carlo step is introduced in the Gibbs sampling strategy. The efficiency of the proposed fusion method is evaluated with respect to several state-of-the-art fusion techniques. In particular, low spatial resolution hyperspectral and multispectral images are fused to produce a high spatial resolution hyperspectral image.