Do More Negative Samples Necessarily Hurt in Contrastive Learning?

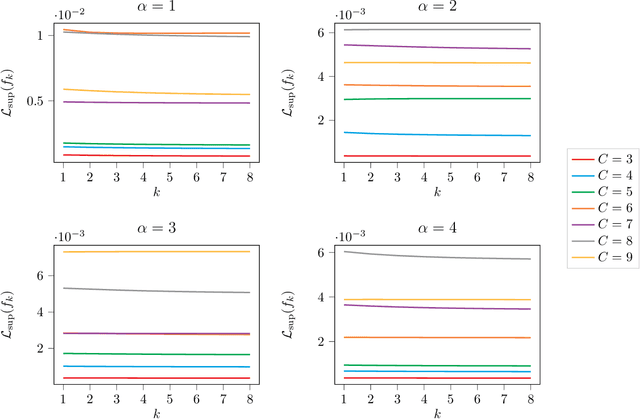
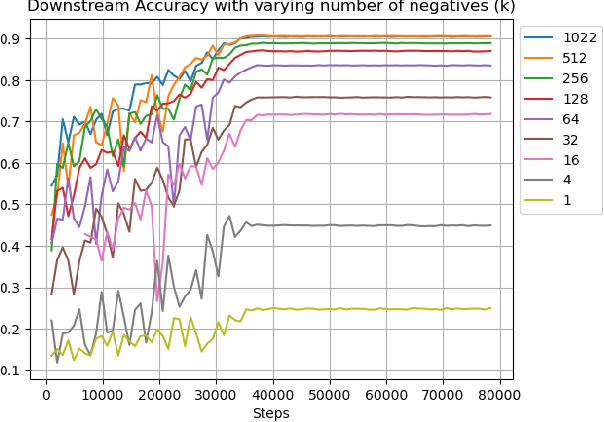
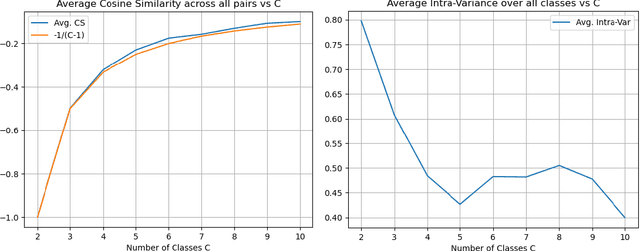
Recent investigations in noise contrastive estimation suggest, both empirically as well as theoretically, that while having more "negative samples" in the contrastive loss improves downstream classification performance initially, beyond a threshold, it hurts downstream performance due to a "collision-coverage" trade-off. But is such a phenomenon inherent in contrastive learning? We show in a simple theoretical setting, where positive pairs are generated by sampling from the underlying latent class (introduced by Saunshi et al. (ICML 2019)), that the downstream performance of the representation optimizing the (population) contrastive loss in fact does not degrade with the number of negative samples. Along the way, we give a structural characterization of the optimal representation in our framework, for noise contrastive estimation. We also provide empirical support for our theoretical results on CIFAR-10 and CIFAR-100 datasets.

Distributionally Robust Data Join

Suppose we are given two datasets: a labeled dataset and unlabeled dataset which also has additional auxiliary features not present in the first dataset. What is the most principled way to use these datasets together to construct a predictor? The answer should depend upon whether these datasets are generated by the same or different distributions over their mutual feature sets, and how similar the test distribution will be to either of those distributions. In many applications, the two datasets will likely follow different distributions, but both may be close to the test distribution. We introduce the problem of building a predictor which minimizes the maximum loss over all probability distributions over the original features, auxiliary features, and binary labels, whose Wasserstein distance is $r_1$ away from the empirical distribution over the labeled dataset and $r_2$ away from that of the unlabeled dataset. This can be thought of as a generalization of distributionally robust optimization (DRO), which allows for two data sources, one of which is unlabeled and may contain auxiliary features.

Agnostic Learnability of Halfspaces via Logistic Loss

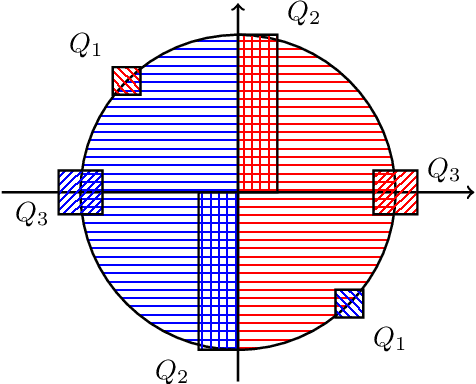
We investigate approximation guarantees provided by logistic regression for the fundamental problem of agnostic learning of homogeneous halfspaces. Previously, for a certain broad class of "well-behaved" distributions on the examples, Diakonikolas et al. (2020) proved an $\tilde{\Omega}(\textrm{OPT})$ lower bound, while Frei et al. (2021) proved an $\tilde{O}(\sqrt{\textrm{OPT}})$ upper bound, where $\textrm{OPT}$ denotes the best zero-one/misclassification risk of a homogeneous halfspace. In this paper, we close this gap by constructing a well-behaved distribution such that the global minimizer of the logistic risk over this distribution only achieves $\Omega(\sqrt{\textrm{OPT}})$ misclassification risk, matching the upper bound in (Frei et al., 2021). On the other hand, we also show that if we impose a radial-Lipschitzness condition in addition to well-behaved-ness on the distribution, logistic regression on a ball of bounded radius reaches $\tilde{O}(\textrm{OPT})$ misclassification risk. Our techniques also show for any well-behaved distribution, regardless of radial Lipschitzness, we can overcome the $\Omega(\sqrt{\textrm{OPT}})$ lower bound for logistic loss simply at the cost of one additional convex optimization step involving the hinge loss and attain $\tilde{O}(\textrm{OPT})$ misclassification risk. This two-step convex optimization algorithm is simpler than previous methods obtaining this guarantee, all of which require solving $O(\log(1/\textrm{OPT}))$ minimization problems.

On the Existence of the Adversarial Bayes Classifier

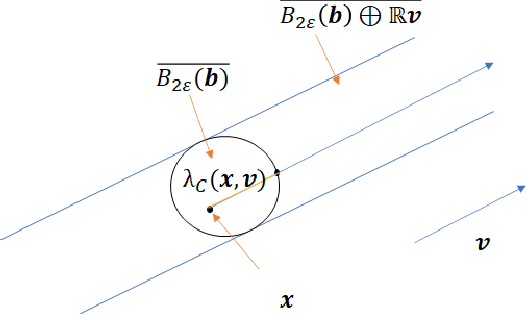
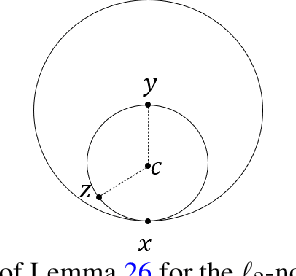
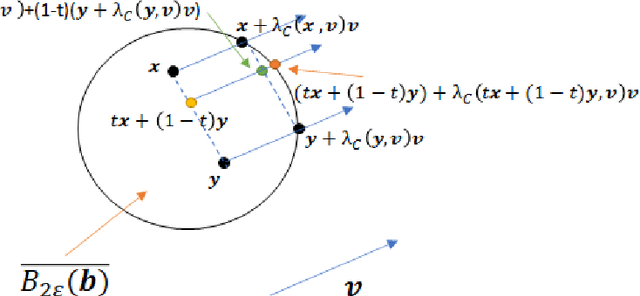
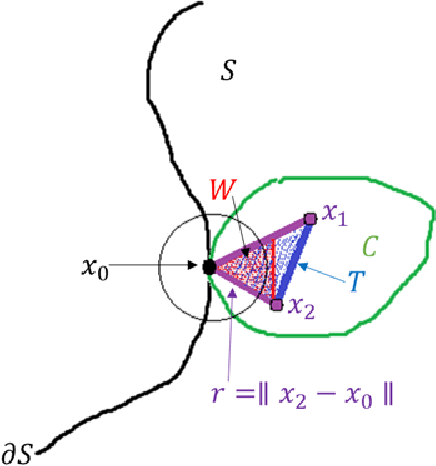
Adversarial robustness is a critical property in a variety of modern machine learning applications. While it has been the subject of several recent theoretical studies, many important questions related to adversarial robustness are still open. In this work, we study a fundamental question regarding Bayes optimality for adversarial robustness. We provide general sufficient conditions under which the existence of a Bayes optimal classifier can be guaranteed for adversarial robustness. Our results can provide a useful tool for a subsequent study of surrogate losses in adversarial robustness and their consistency properties. This manuscript is the extended version of the paper "On the Existence of the Adversarial Bayes Classifier" published in NeurIPS. The results of the original paper did not apply to some non-strictly convex norms. Here we extend our results to all possible norms.

Efficient Algorithms for Learning Depth-2 Neural Networks with General ReLU Activations

We present polynomial time and sample efficient algorithms for learning an unknown depth-2 feedforward neural network with general ReLU activations, under mild non-degeneracy assumptions. In particular, we consider learning an unknown network of the form $f(x) = {a}^{\mathsf{T}}\sigma({W}^\mathsf{T}x+b)$, where $x$ is drawn from the Gaussian distribution, and $\sigma(t) := \max(t,0)$ is the ReLU activation. Prior works for learning networks with ReLU activations assume that the bias $b$ is zero. In order to deal with the presence of the bias terms, our proposed algorithm consists of robustly decomposing multiple higher order tensors arising from the Hermite expansion of the function $f(x)$. Using these ideas we also establish identifiability of the network parameters under minimal assumptions.

On the benefits of maximum likelihood estimation for Regression and Forecasting

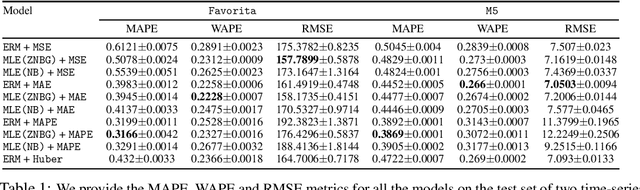
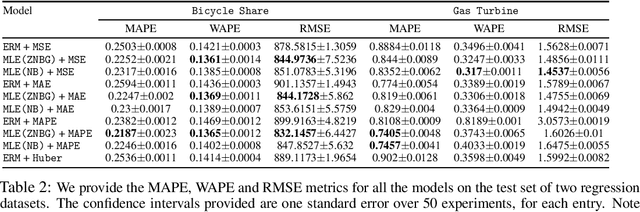
We advocate for a practical Maximum Likelihood Estimation (MLE) approach for regression and forecasting, as an alternative to the typical approach of Empirical Risk Minimization (ERM) for a specific target metric. This approach is better suited to capture inductive biases such as prior domain knowledge in datasets, and can output post-hoc estimators at inference time that can optimize different types of target metrics. We present theoretical results to demonstrate that our approach is always competitive with any estimator for the target metric under some general conditions, and in many practical settings (such as Poisson Regression) can actually be much superior to ERM. We demonstrate empirically that our method instantiated with a well-designed general purpose mixture likelihood family can obtain superior performance over ERM for a variety of tasks across time-series forecasting and regression datasets with different data distributions.

Semi-supervised Active Regression

Labelled data often comes at a high cost as it may require recruiting human labelers or running costly experiments. At the same time, in many practical scenarios, one already has access to a partially labelled, potentially biased dataset that can help with the learning task at hand. Motivated by such settings, we formally initiate a study of $semi-supervised$ $active$ $learning$ through the frame of linear regression. In this setting, the learner has access to a dataset $X \in \mathbb{R}^{(n_1+n_2) \times d}$ which is composed of $n_1$ unlabelled examples that an algorithm can actively query, and $n_2$ examples labelled a-priori. Concretely, denoting the true labels by $Y \in \mathbb{R}^{n_1 + n_2}$, the learner's objective is to find $\widehat{\beta} \in \mathbb{R}^d$ such that, \begin{equation} \| X \widehat{\beta} - Y \|_2^2 \le (1 + \epsilon) \min_{\beta \in \mathbb{R}^d} \| X \beta - Y \|_2^2 \end{equation} while making as few additional label queries as possible. In order to bound the label queries, we introduce an instance dependent parameter called the reduced rank, denoted by $R_X$, and propose an efficient algorithm with query complexity $O(R_X/\epsilon)$. This result directly implies improved upper bounds for two important special cases: (i) active ridge regression, and (ii) active kernel ridge regression, where the reduced-rank equates to the statistical dimension, $sd_\lambda$ and effective dimension, $d_\lambda$ of the problem respectively, where $\lambda \ge 0$ denotes the regularization parameter. For active ridge regression we also prove a matching lower bound of $O(sd_\lambda / \epsilon)$ on the query complexity of any algorithm. This subsumes prior work that only considered the unregularized case, i.e., $\lambda = 0$.

Neural Active Learning with Performance Guarantees

We investigate the problem of active learning in the streaming setting in non-parametric regimes, where the labels are stochastically generated from a class of functions on which we make no assumptions whatsoever. We rely on recently proposed Neural Tangent Kernel (NTK) approximation tools to construct a suitable neural embedding that determines the feature space the algorithm operates on and the learned model computed atop. Since the shape of the label requesting threshold is tightly related to the complexity of the function to be learned, which is a-priori unknown, we also derive a version of the algorithm which is agnostic to any prior knowledge. This algorithm relies on a regret balancing scheme to solve the resulting online model selection problem, and is computationally efficient. We prove joint guarantees on the cumulative regret and number of requested labels which depend on the complexity of the labeling function at hand. In the linear case, these guarantees recover known minimax results of the generalization error as a function of the label complexity in a standard statistical learning setting.

Measuring Model Fairness under Noisy Covariates: A Theoretical Perspective

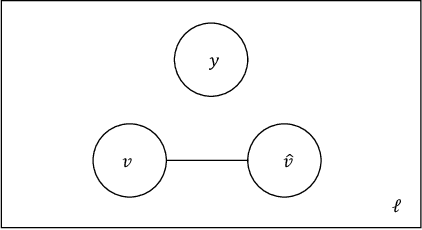
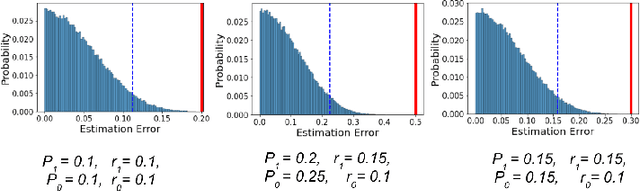
In this work we study the problem of measuring the fairness of a machine learning model under noisy information. Focusing on group fairness metrics, we investigate the particular but common situation when the evaluation requires controlling for the confounding effect of covariate variables. In a practical setting, we might not be able to jointly observe the covariate and group information, and a standard workaround is to then use proxies for one or more of these variables. Prior works have demonstrated the challenges with using a proxy for sensitive attributes, and strong independence assumptions are needed to provide guarantees on the accuracy of the noisy estimates. In contrast, in this work we study using a proxy for the covariate variable and present a theoretical analysis that aims to characterize weaker conditions under which accurate fairness evaluation is possible. Furthermore, our theory identifies potential sources of errors and decouples them into two interpretable parts $\gamma$ and $\epsilon$. The first part $\gamma$ depends solely on the performance of the proxy such as precision and recall, whereas the second part $\epsilon$ captures correlations between all the variables of interest. We show that in many scenarios the error in the estimates is dominated by $\gamma$ via a linear dependence, whereas the dependence on the correlations $\epsilon$ only constitutes a lower order term. As a result we expand the understanding of scenarios where measuring model fairness via proxies can be an effective approach. Finally, we compare, via simulations, the theoretical upper-bounds to the distribution of simulated estimation errors and show that assuming some structure on the data, even weak, is key to significantly improve both theoretical guarantees and empirical results.

A Finer Calibration Analysis for Adversarial Robustness

We present a more general analysis of $H$-calibration for adversarially robust classification. By adopting a finer definition of calibration, we can cover settings beyond the restricted hypothesis sets studied in previous work. In particular, our results hold for most common hypothesis sets used in machine learning. We both fix some previous calibration results (Bao et al., 2020) and generalize others (Awasthi et al., 2021). Moreover, our calibration results, combined with the previous study of consistency by Awasthi et al. (2021), also lead to more general $H$-consistency results covering common hypothesis sets.