Geomstats: A Python Package for Riemannian Geometry in Machine Learning

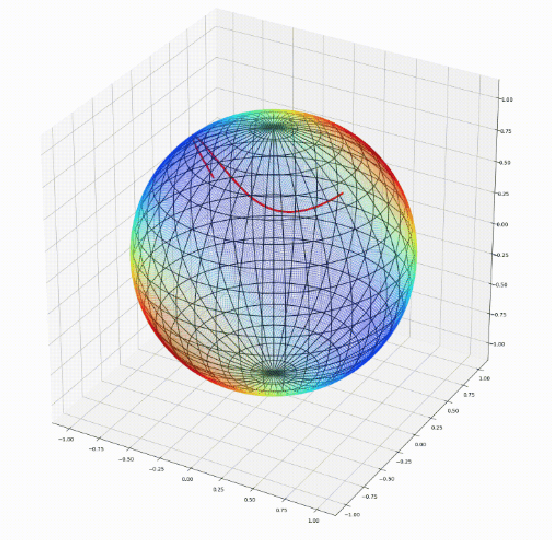
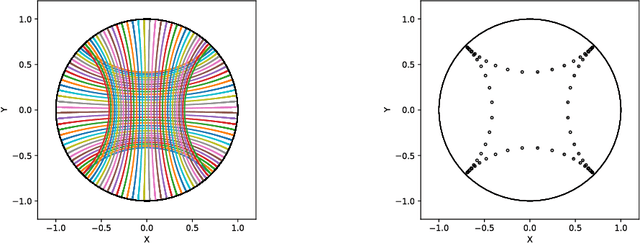
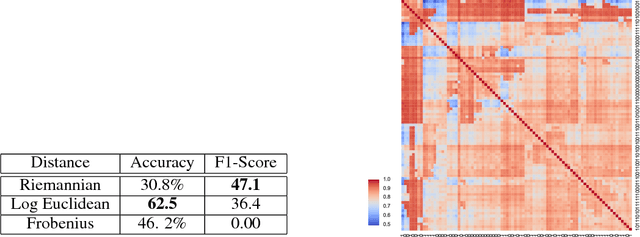
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.

Adversarial Risk Bounds for Neural Networks through Sparsity based Compression

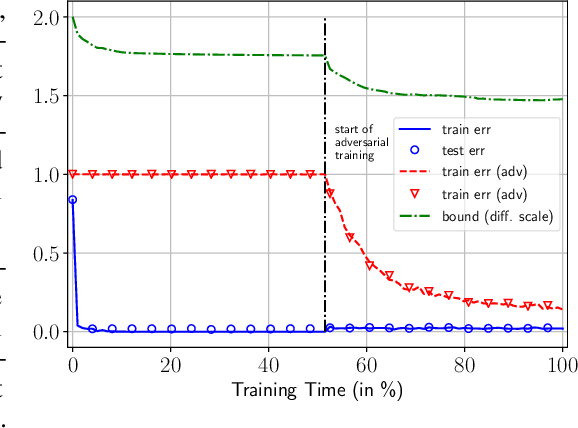
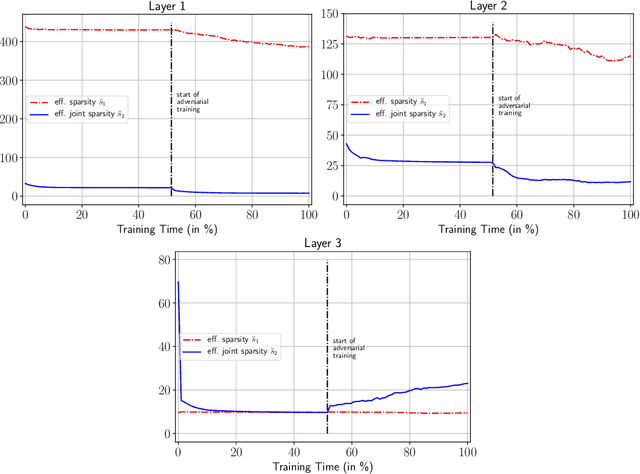
Neural networks have been shown to be vulnerable against minor adversarial perturbations of their inputs, especially for high dimensional data under $\ell_\infty$ attacks. To combat this problem, techniques like adversarial training have been employed to obtain models which are robust on the training set. However, the robustness of such models against adversarial perturbations may not generalize to unseen data. To study how robustness generalizes, recent works assume that the inputs have bounded $\ell_2$-norm in order to bound the adversarial risk for $\ell_\infty$ attacks with no explicit dimension dependence. In this work we focus on $\ell_\infty$ attacks on $\ell_\infty$ bounded inputs and prove margin-based bounds. Specifically, we use a compression based approach that relies on efficiently compressing the set of tunable parameters without distorting the adversarial risk. To achieve this, we apply the concept of effective sparsity and effective joint sparsity on the weight matrices of neural networks. This leads to bounds with no explicit dependence on the input dimension, neither on the number of classes. Our results show that neural networks with approximately sparse weight matrices not only enjoy enhanced robustness, but also better generalization.

Pymanopt: A Python Toolbox for Optimization on Manifolds using Automatic Differentiation

Optimization on manifolds is a class of methods for optimization of an objective function, subject to constraints which are smooth, in the sense that the set of points which satisfy the constraints admits the structure of a differentiable manifold. While many optimization problems are of the described form, technicalities of differential geometry and the laborious calculation of derivatives pose a significant barrier for experimenting with these methods. We introduce Pymanopt (available at https://pymanopt.github.io), a toolbox for optimization on manifolds, implemented in Python, that---similarly to the Manopt Matlab toolbox---implements several manifold geometries and optimization algorithms. Moreover, we lower the barriers to users further by using automated differentiation for calculating derivative information, saving users time and saving them from potential calculation and implementation errors.