A Classical View on Benign Overfitting: The Role of Sample Size

Benign overfitting is a phenomenon in machine learning where a model perfectly fits (interpolates) the training data, including noisy examples, yet still generalizes well to unseen data. Understanding this phenomenon has attracted considerable attention in recent years. In this work, we introduce a conceptual shift, by focusing on almost benign overfitting, where models simultaneously achieve both arbitrarily small training and test errors. This behavior is characteristic of neural networks, which often achieve low (but non-zero) training error while still generalizing well. We hypothesize that this almost benign overfitting can emerge even in classical regimes, by analyzing how the interaction between sample size and model complexity enables larger models to achieve both good training fit but still approach Bayes-optimal generalization. We substantiate this hypothesis with theoretical evidence from two case studies: (i) kernel ridge regression, and (ii) least-squares regression using a two-layer fully connected ReLU neural network trained via gradient flow. In both cases, we overcome the strong assumptions often required in prior work on benign overfitting. Our results on neural networks also provide the first generalization result in this setting that does not rely on any assumptions about the underlying regression function or noise, beyond boundedness. Our analysis introduces a novel proof technique based on decomposing the excess risk into estimation and approximation errors, interpreting gradient flow as an implicit regularizer, that helps avoid uniform convergence traps. This analysis idea could be of independent interest.

Benign Overfitting for Regression with Trained Two-Layer ReLU Networks

We study the least-square regression problem with a two-layer fully-connected neural network, with ReLU activation function, trained by gradient flow. Our first result is a generalization result, that requires no assumptions on the underlying regression function or the noise other than that they are bounded. We operate in the neural tangent kernel regime, and our generalization result is developed via a decomposition of the excess risk into estimation and approximation errors, viewing gradient flow as an implicit regularizer. This decomposition in the context of neural networks is a novel perspective of gradient descent, and helps us avoid uniform convergence traps. In this work, we also establish that under the same setting, the trained network overfits to the data. Together, these results, establishes the first result on benign overfitting for finite-width ReLU networks for arbitrary regression functions.

Score matching through the roof: linear, nonlinear, and latent variables causal discovery

Causal discovery from observational data holds great promise, but existing methods rely on strong assumptions about the underlying causal structure, often requiring full observability of all relevant variables. We tackle these challenges by leveraging the score function $\nabla \log p(X)$ of observed variables for causal discovery and propose the following contributions. First, we generalize the existing results of identifiability with the score to additive noise models with minimal requirements on the causal mechanisms. Second, we establish conditions for inferring causal relations from the score even in the presence of hidden variables; this result is two-faced: we demonstrate the score's potential as an alternative to conditional independence tests to infer the equivalence class of causal graphs with hidden variables, and we provide the necessary conditions for identifying direct causes in latent variable models. Building on these insights, we propose a flexible algorithm for causal discovery across linear, nonlinear, and latent variable models, which we empirically validate.

Testing Granger Non-Causality in Panels with Cross-Sectional Dependencies

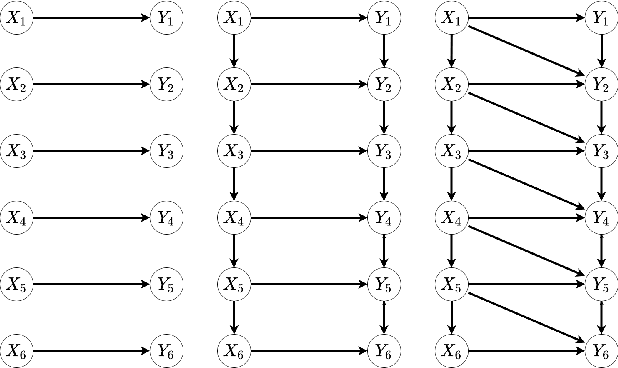
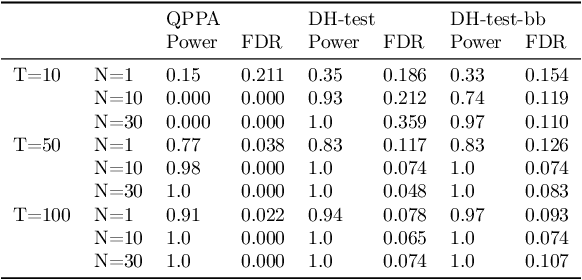
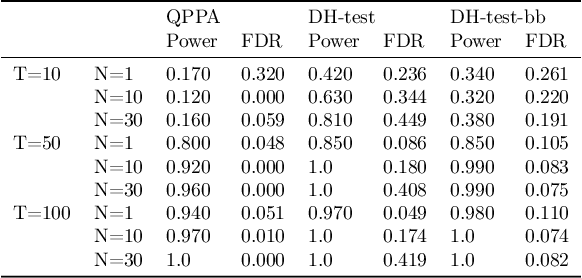
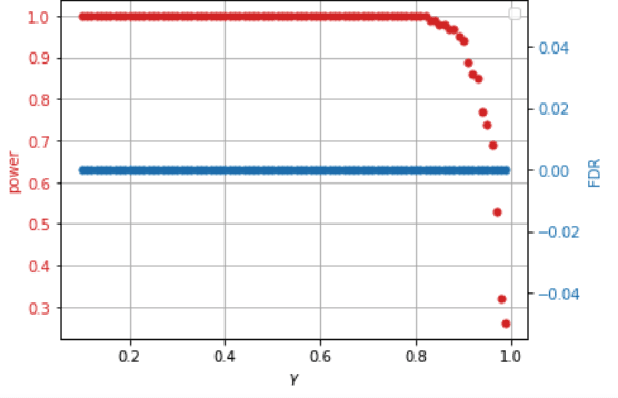
This paper proposes a new approach for testing Granger non-causality on panel data. Instead of aggregating panel member statistics, we aggregate their corresponding p-values and show that the resulting p-value approximately bounds the type I error by the chosen significance level even if the panel members are dependent. We compare our approach against the most widely used Granger causality algorithm on panel data and show that our approach yields lower FDR at the same power for large sample sizes and panels with cross-sectional dependencies. Finally, we examine COVID-19 data about confirmed cases and deaths measured in countries/regions worldwide and show that our approach is able to discover the true causal relation between confirmed cases and deaths while state-of-the-art approaches fail.

Why did the distribution change?

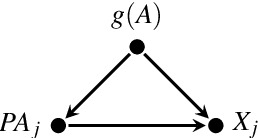
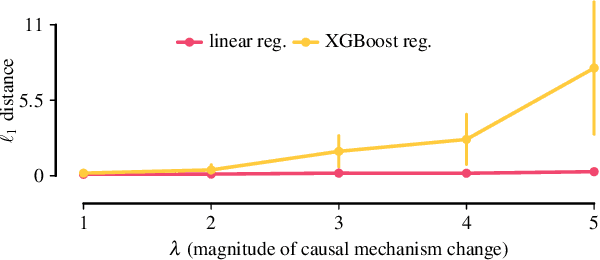
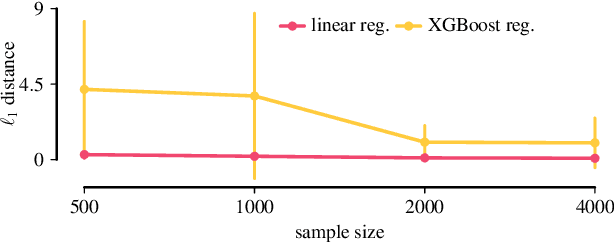
We describe a formal approach based on graphical causal models to identify the "root causes" of the change in the probability distribution of variables. After factorizing the joint distribution into conditional distributions of each variable, given its parents (the "causal mechanisms"), we attribute the change to changes of these causal mechanisms. This attribution analysis accounts for the fact that mechanisms often change independently and sometimes only some of them change. Through simulations, we study the performance of our distribution change attribution method. We then present a real-world case study identifying the drivers of the difference in the income distribution between men and women.