Omer Tamuz
Efficient Bayesian Learning in Social Networks with Gaussian Estimators
Jun 26, 2016Abstract:We consider a group of Bayesian agents who try to estimate a state of the world $\theta$ through interaction on a social network. Each agent $v$ initially receives a private measurement of $\theta$: a number $S_v$ picked from a Gaussian distribution with mean $\theta$ and standard deviation one. Then, in each discrete time iteration, each reveals its estimate of $\theta$ to its neighbors, and, observing its neighbors' actions, updates its belief using Bayes' Law. This process aggregates information efficiently, in the sense that all the agents converge to the belief that they would have, had they access to all the private measurements. We show that this process is computationally efficient, so that each agent's calculation can be easily carried out. We also show that on any graph the process converges after at most $2N \cdot D$ steps, where $N$ is the number of agents and $D$ is the diameter of the network. Finally, we show that on trees and on distance transitive-graphs the process converges after $D$ steps, and that it preserves privacy, so that agents learn very little about the private signal of most other agents, despite the efficient aggregation of information. Our results extend those in an unpublished manuscript of the first and last authors.
Textual Features for Programming by Example
Sep 17, 2012


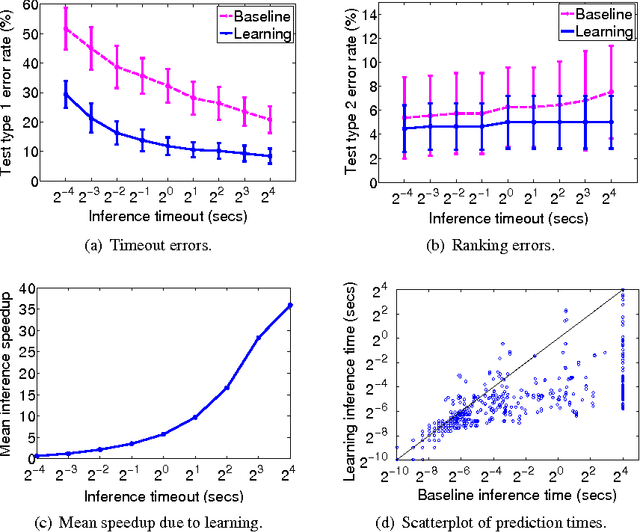
Abstract:In Programming by Example, a system attempts to infer a program from input and output examples, generally by searching for a composition of certain base functions. Performing a naive brute force search is infeasible for even mildly involved tasks. We note that the examples themselves often present clues as to which functions to compose, and how to rank the resulting programs. In text processing, which is our domain of interest, clues arise from simple textual features: for example, if parts of the input and output strings are permutations of one another, this suggests that sorting may be useful. We describe a system that learns the reliability of such clues, allowing for faster search and a principled ranking over programs. Experiments on a prototype of this system show that this learning scheme facilitates efficient inference on a range of text processing tasks.
Adaptively Learning the Crowd Kernel
Jun 25, 2011
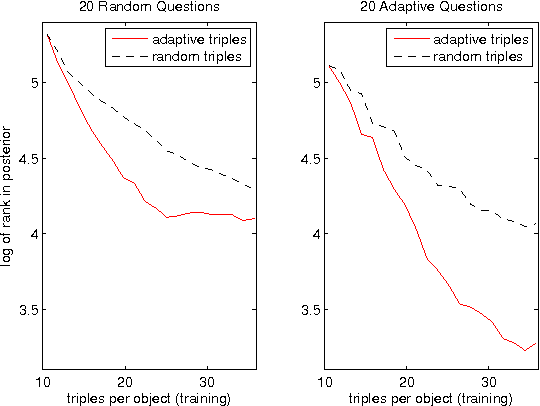


Abstract:We introduce an algorithm that, given n objects, learns a similarity matrix over all n^2 pairs, from crowdsourced data alone. The algorithm samples responses to adaptively chosen triplet-based relative-similarity queries. Each query has the form "is object 'a' more similar to 'b' or to 'c'?" and is chosen to be maximally informative given the preceding responses. The output is an embedding of the objects into Euclidean space (like MDS); we refer to this as the "crowd kernel." SVMs reveal that the crowd kernel captures prominent and subtle features across a number of domains, such as "is striped" among neckties and "vowel vs. consonant" among letters.
* 9 pages, 7 figures, Accepted to the 28th International Conference on Machine Learning (ICML), 2011
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge