Spectral Embedding via Chebyshev Bases for Robust DeepONet Approximation

Deep Operator Networks (DeepONets) have become a central tool in data-driven operator learning, providing flexible surrogates for nonlinear mappings arising in partial differential equations (PDEs). However, the standard trunk design based on fully connected layers acting on raw spatial or spatiotemporal coordinates struggles to represent sharp gradients, boundary layers, and non-periodic structures commonly found in PDEs posed on bounded domains with Dirichlet or Neumann boundary conditions. To address these limitations, we introduce the Spectral-Embedded DeepONet (SEDONet), a new DeepONet variant in which the trunk is driven by a fixed Chebyshev spectral dictionary rather than coordinate inputs. This non-periodic spectral embedding provides a principled inductive bias tailored to bounded domains, enabling the learned operator to capture fine-scale non-periodic features that are difficult for Fourier or MLP trunks to represent. SEDONet is evaluated on a suite of PDE benchmarks including 2D Poisson, 1D Burgers, 1D advection-diffusion, Allen-Cahn dynamics, and the Lorenz-96 chaotic system, covering elliptic, parabolic, advective, and multiscale temporal phenomena, all of which can be viewed as canonical problems in computational mechanics. Across all datasets, SEDONet consistently achieves the lowest relative L2 errors among DeepONet, FEDONet, and SEDONet, with average improvements of about 30-40% over the baseline DeepONet and meaningful gains over Fourier-embedded variants on non-periodic geometries. Spectral analyses further show that SEDONet more accurately preserves high-frequency and boundary-localized features, demonstrating the value of Chebyshev embeddings in non-periodic operator learning. The proposed architecture offers a simple, parameter-neutral modification to DeepONets, delivering a robust and efficient spectral framework for surrogate modeling of PDEs on bounded domains.

Method of Manufactured Learning for Solver-free Training of Neural Operators

Training neural operators to approximate mappings between infinite-dimensional function spaces often requires extensive datasets generated by either demanding experimental setups or computationally expensive numerical solvers. This dependence on solver-based data limits scalability and constrains exploration across physical systems. Here we introduce the Method of Manufactured Learning (MML), a solver-independent framework for training neural operators using analytically constructed, physics-consistent datasets. Inspired by the classical method of manufactured solutions, MML replaces numerical data generation with functional synthesis, i.e., smooth candidate solutions are sampled from controlled analytical spaces, and the corresponding forcing fields are derived by direct application of the governing differential operators. During inference, setting these forcing terms to zero restores the original governing equations, allowing the trained neural operator to emulate the true solution operator of the system. The framework is agnostic to network architecture and can be integrated with any operator learning paradigm. In this paper, we employ Fourier neural operator as a representative example. Across canonical benchmarks including heat, advection, Burgers, and diffusion-reaction equations. MML achieves high spectral accuracy, low residual errors, and strong generalization to unseen conditions. By reframing data generation as a process of analytical synthesis, MML offers a scalable, solver-agnostic pathway toward constructing physically grounded neural operators that retain fidelity to governing laws without reliance on expensive numerical simulations or costly experimental data for training.

FEDONet : Fourier-Embedded DeepONet for Spectrally Accurate Operator Learning

Deep Operator Networks (DeepONets) have recently emerged as powerful data-driven frameworks for learning nonlinear operators, particularly suited for approximating solutions to partial differential equations (PDEs). Despite their promising capabilities, the standard implementation of DeepONets, which typically employs fully connected linear layers in the trunk network, can encounter limitations in capturing complex spatial structures inherent to various PDEs. To address this, we introduce Fourier-embedded trunk networks within the DeepONet architecture, leveraging random Fourier feature mappings to enrich spatial representation capabilities. Our proposed Fourier-embedded DeepONet, FEDONet demonstrates superior performance compared to the traditional DeepONet across a comprehensive suite of PDE-driven datasets, including the two-dimensional Poisson equation, Burgers' equation, the Lorenz-63 chaotic system, Eikonal equation, Allen-Cahn equation, Kuramoto-Sivashinsky equation, and the Lorenz-96 system. Empirical evaluations of FEDONet consistently show significant improvements in solution reconstruction accuracy, with average relative L2 performance gains ranging between 2-3x compared to the DeepONet baseline. This study highlights the effectiveness of Fourier embeddings in enhancing neural operator learning, offering a robust and broadly applicable methodology for PDE surrogate modeling.

Machine Learning for enhancing Wind Field Resolution in Complex Terrain

Atmospheric flows are governed by a broad variety of spatio-temporal scales, thus making real-time numerical modeling of such turbulent flows in complex terrain at high resolution computationally intractable. In this study, we demonstrate a neural network approach motivated by Enhanced Super-Resolution Generative Adversarial Networks to upscale low-resolution wind fields to generate high-resolution wind fields in an actual wind farm in Bessaker, Norway. The neural network-based model is shown to successfully reconstruct fully resolved 3D velocity fields from a coarser scale while respecting the local terrain and that it easily outperforms trilinear interpolation. We also demonstrate that by using appropriate cost function based on domain knowledge, we can alleviate the use of adversarial training.

SuperBench: A Super-Resolution Benchmark Dataset for Scientific Machine Learning

Super-Resolution (SR) techniques aim to enhance data resolution, enabling the retrieval of finer details, and improving the overall quality and fidelity of the data representation. There is growing interest in applying SR methods to complex spatiotemporal systems within the Scientific Machine Learning (SciML) community, with the hope of accelerating numerical simulations and/or improving forecasts in weather, climate, and related areas. However, the lack of standardized benchmark datasets for comparing and validating SR methods hinders progress and adoption in SciML. To address this, we introduce SuperBench, the first benchmark dataset featuring high-resolution datasets (up to $2048\times2048$ dimensions), including data from fluid flows, cosmology, and weather. Here, we focus on validating spatial SR performance from data-centric and physics-preserved perspectives, as well as assessing robustness to data degradation tasks. While deep learning-based SR methods (developed in the computer vision community) excel on certain tasks, despite relatively limited prior physics information, we identify limitations of these methods in accurately capturing intricate fine-scale features and preserving fundamental physical properties and constraints in scientific data. These shortcomings highlight the importance and subtlety of incorporating domain knowledge into ML models. We anticipate that SuperBench will significantly advance SR methods for scientific tasks.

Digital Twins in Wind Energy: Emerging Technologies and Industry-Informed Future Directions

This article presents a comprehensive overview of the digital twin technology and its capability levels, with a specific focus on its applications in the wind energy industry. It consolidates the definitions of digital twin and its capability levels on a scale from 0-5; 0-standalone, 1-descriptive, 2-diagnostic, 3-predictive, 4-prescriptive, 5-autonomous. It then, from an industrial perspective, identifies the current state of the art and research needs in the wind energy sector. The article proposes approaches to the identified challenges from the perspective of research institutes and offers a set of recommendations for diverse stakeholders to facilitate the acceptance of the technology. The contribution of this article lies in its synthesis of the current state of knowledge and its identification of future research needs and challenges from an industry perspective, ultimately providing a roadmap for future research and development in the field of digital twin and its applications in the wind energy industry.

Artificial intelligence-driven digital twin of a modern house demonstrated in virtual reality

A digital twin is defined as a virtual representation of a physical asset enabled through data and simulators for real-time prediction, optimization, monitoring, controlling, and improved decision-making. Unfortunately, the term remains vague and says little about its capability. Recently, the concept of capability level has been introduced to address this issue. Based on its capability, the concept states that a digital twin can be categorized on a scale from zero to five, referred to as standalone, descriptive, diagnostic, predictive, prescriptive, and autonomous, respectively. The current work introduces the concept in the context of the built environment. It demonstrates the concept by using a modern house as a use case. The house is equipped with an array of sensors that collect timeseries data regarding the internal state of the house. Together with physics-based and data-driven models, these data are used to develop digital twins at different capability levels demonstrated in virtual reality. The work, in addition to presenting a blueprint for developing digital twins, also provided future research directions to enhance the technology.

Prospects of federated machine learning in fluid dynamics

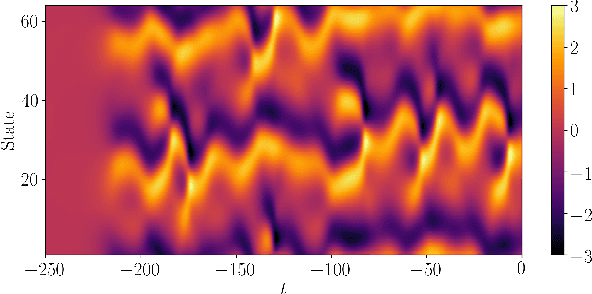
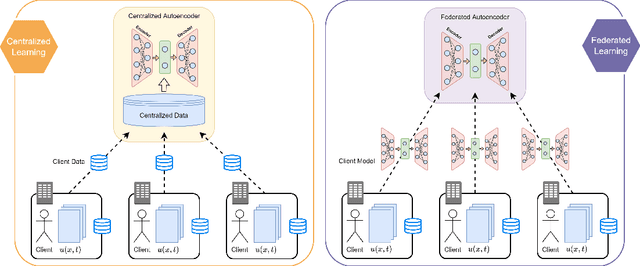
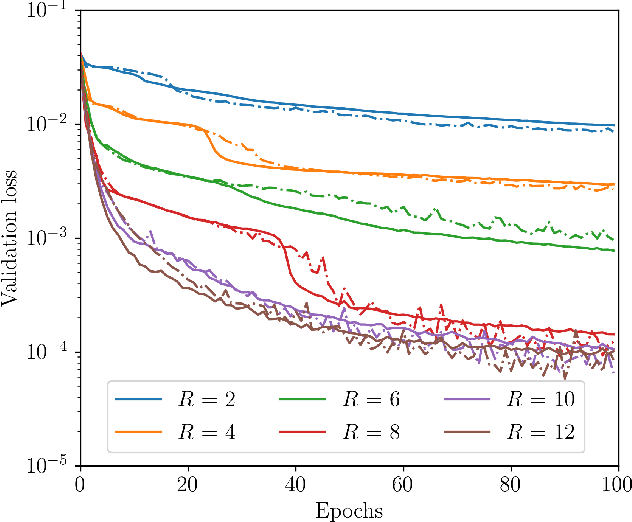
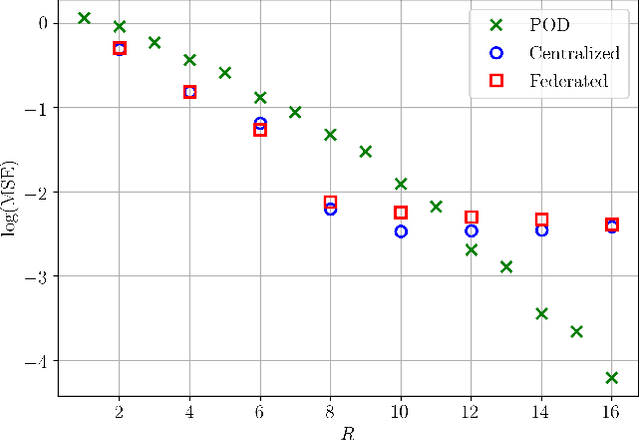
Physics-based models have been mainstream in fluid dynamics for developing predictive models. In recent years, machine learning has offered a renaissance to the fluid community due to the rapid developments in data science, processing units, neural network based technologies, and sensor adaptations. So far in many applications in fluid dynamics, machine learning approaches have been mostly focused on a standard process that requires centralizing the training data on a designated machine or in a data center. In this letter, we present a federated machine learning approach that enables localized clients to collaboratively learn an aggregated and shared predictive model while keeping all the training data on each edge device. We demonstrate the feasibility and prospects of such decentralized learning approach with an effort to forge a deep learning surrogate model for reconstructing spatiotemporal fields. Our results indicate that federated machine learning might be a viable tool for designing highly accurate predictive decentralized digital twins relevant to fluid dynamics.

Digital Twin Data Modelling by Randomized Orthogonal Decomposition and Deep Learning

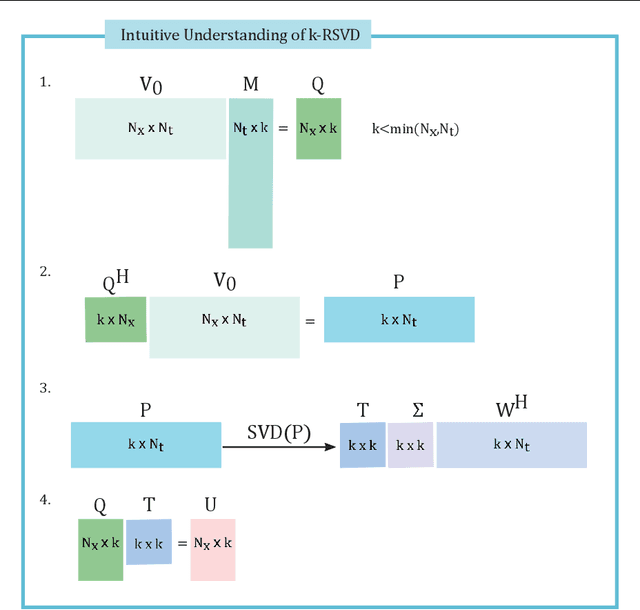
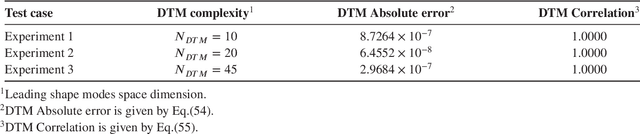
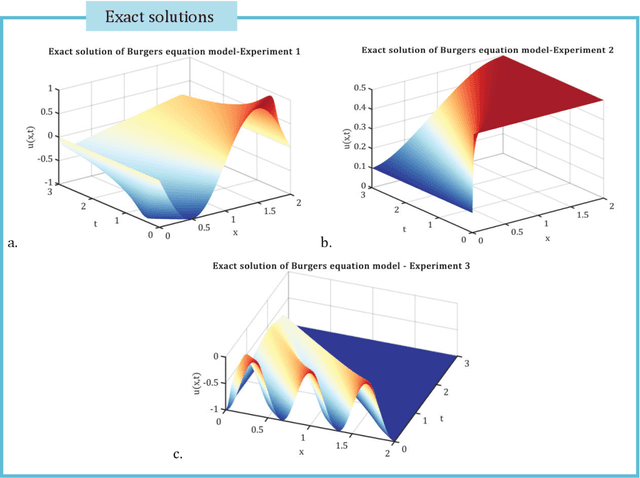
A digital twin is a surrogate model that has the main feature to mirror the original process behavior. Associating the dynamical process with a digital twin model of reduced complexity has the significant advantage to map the dynamics with high accuracy and reduced costs in CPU time and hardware to timescales over which that suffers significantly changes and so it is difficult to explore. This paper introduces a new framework for creating efficient digital twin models of fluid flows. We introduce a novel algorithm that combines the advantages of Krylov based dynamic mode decomposition with proper orthogonal decomposition and outperforms the selection of the most influential modes. We prove that randomized orthogonal decomposition algorithm provides several advantages over SVD empirical orthogonal decomposition methods and mitigates the projection error formulating a multiobjective optimization problem.We involve the state-of-the-art artificial intelligence Deep Learning (DL) to perform a real-time adaptive calibration of the digital twin model, with increasing fidelity. The output is a high-fidelity DIGITAL TWIN DATA MODEL of the fluid flow dynamics, with the advantage of a reduced complexity. The new modelling tools are investigated in the numerical simulation of three wave phenomena with increasing complexity. We show that the outputs are consistent with the original source data.We perform a thorough assessment of the performance of the new digital twin data models, in terms of numerical accuracy and computational efficiency, including a time simulation response feature study.

Combining physics-based and data-driven techniques for reliable hybrid analysis and modeling using the corrective source term approach

Upcoming technologies like digital twins, autonomous, and artificial intelligent systems involving safety-critical applications require models which are accurate, interpretable, computationally efficient, and generalizable. Unfortunately, the two most commonly used modeling approaches, physics-based modeling (PBM) and data-driven modeling (DDM) fail to satisfy all these requirements. In the current work, we demonstrate how a hybrid approach combining the best of PBM and DDM can result in models which can outperform them both. We do so by combining partial differential equations based on first principles describing partially known physics with a black box DDM, in this case, a deep neural network model compensating for the unknown physics. First, we present a mathematical argument for why this approach should work and then apply the hybrid approach to model two dimensional heat diffusion problem with an unknown source term. The result demonstrates the method's superior performance in terms of accuracy, and generalizability. Additionally, it is shown how the DDM part can be interpreted within the hybrid framework to make the overall approach reliable.