Certified Per-Instance Unlearning Using Individual Sensitivity Bounds

Certified machine unlearning can be achieved via noise injection leading to differential privacy guarantees, where noise is calibrated to worst-case sensitivity. Such conservative calibration often results in performance degradation, limiting practical applicability. In this work, we investigate an alternative approach based on adaptive per-instance noise calibration tailored to the individual contribution of each data point to the learned solution. This raises the following challenge: how can one establish formal unlearning guarantees when the mechanism depends on the specific point to be removed? To define individual data point sensitivities in noisy gradient dynamics, we consider the use of per-instance differential privacy. For ridge regression trained via Langevin dynamics, we derive high-probability per-instance sensitivity bounds, yielding certified unlearning with substantially less noise injection. We corroborate our theoretical findings through experiments in linear settings and provide further empirical evidence on the relevance of the approach in deep learning settings.

Generalized Leverage Score for Scalable Assessment of Privacy Vulnerability

Can the privacy vulnerability of individual data points be assessed without retraining models or explicitly simulating attacks? We answer affirmatively by showing that exposure to membership inference attack (MIA) is fundamentally governed by a data point's influence on the learned model. We formalize this in the linear setting by establishing a theoretical correspondence between individual MIA risk and the leverage score, identifying it as a principled metric for vulnerability. This characterization explains how data-dependent sensitivity translates into exposure, without the computational burden of training shadow models. Building on this, we propose a computationally efficient generalization of the leverage score for deep learning. Empirical evaluations confirm a strong correlation between the proposed score and MIA success, validating this metric as a practical surrogate for individual privacy risk assessment.

Learning To Sample From Diffusion Models Via Inverse Reinforcement Learning

Diffusion models generate samples through an iterative denoising process, guided by a neural network. While training the denoiser on real-world data is computationally demanding, the sampling procedure itself is more flexible. This adaptability serves as a key lever in practice, enabling improvements in both the quality of generated samples and the efficiency of the sampling process. In this work, we introduce an inverse reinforcement learning framework for learning sampling strategies without retraining the denoiser. We formulate the diffusion sampling procedure as a discrete-time finite-horizon Markov Decision Process, where actions correspond to optional modifications of the sampling dynamics. To optimize action scheduling, we avoid defining an explicit reward function. Instead, we directly match the target behavior expected from the sampler using policy gradient techniques. We provide experimental evidence that this approach can improve the quality of samples generated by pretrained diffusion models and automatically tune sampling hyperparameters.

Memorization in Fine-Tuned Large Language Models

This study investigates the mechanisms and factors influencing memorization in fine-tuned large language models (LLMs), with a focus on the medical domain due to its privacy-sensitive nature. We examine how different aspects of the fine-tuning process affect a model's propensity to memorize training data, using the PHEE dataset of pharmacovigilance events. Our research employs two main approaches: a membership inference attack to detect memorized data, and a generation task with prompted prefixes to assess verbatim reproduction. We analyze the impact of adapting different weight matrices in the transformer architecture, the relationship between perplexity and memorization, and the effect of increasing the rank in low-rank adaptation (LoRA) fine-tuning. Key findings include: (1) Value and Output matrices contribute more significantly to memorization compared to Query and Key matrices; (2) Lower perplexity in the fine-tuned model correlates with increased memorization; (3) Higher LoRA ranks lead to increased memorization, but with diminishing returns at higher ranks. These results provide insights into the trade-offs between model performance and privacy risks in fine-tuned LLMs. Our findings have implications for developing more effective and responsible strategies for adapting large language models while managing data privacy concerns.

Optimal Classification under Performative Distribution Shift

Performative learning addresses the increasingly pervasive situations in which algorithmic decisions may induce changes in the data distribution as a consequence of their public deployment. We propose a novel view in which these performative effects are modelled as push-forward measures. This general framework encompasses existing models and enables novel performative gradient estimation methods, leading to more efficient and scalable learning strategies. For distribution shifts, unlike previous models which require full specification of the data distribution, we only assume knowledge of the shift operator that represents the performative changes. This approach can also be integrated into various change-of-variablebased models, such as VAEs or normalizing flows. Focusing on classification with a linear-in-parameters performative effect, we prove the convexity of the performative risk under a new set of assumptions. Notably, we do not limit the strength of performative effects but rather their direction, requiring only that classification becomes harder when deploying more accurate models. In this case, we also establish a connection with adversarially robust classification by reformulating the minimization of the performative risk as a min-max variational problem. Finally, we illustrate our approach on synthetic and real datasets.

A/B/n Testing with Control in the Presence of Subpopulations

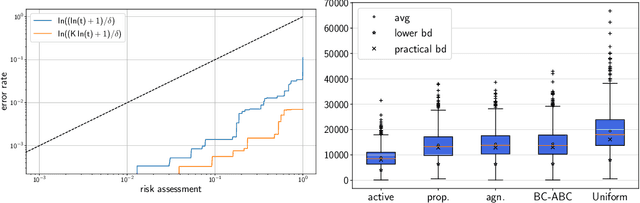
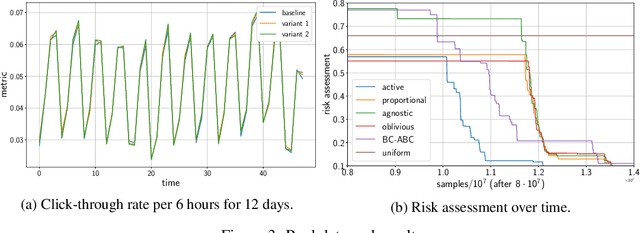
Motivated by A/B/n testing applications, we consider a finite set of distributions (called \emph{arms}), one of which is treated as a \emph{control}. We assume that the population is stratified into homogeneous subpopulations. At every time step, a subpopulation is sampled and an arm is chosen: the resulting observation is an independent draw from the arm conditioned on the subpopulation. The quality of each arm is assessed through a weighted combination of its subpopulation means. We propose a strategy for sequentially choosing one arm per time step so as to discover as fast as possible which arms, if any, have higher weighted expectation than the control. This strategy is shown to be asymptotically optimal in the following sense: if $\tau_\delta$ is the first time when the strategy ensures that it is able to output the correct answer with probability at least $1-\delta$, then $\mathbb{E}[\tau_\delta]$ grows linearly with $\log(1/\delta)$ at the exact optimal rate. This rate is identified in the paper in three different settings: (1) when the experimenter does not observe the subpopulation information, (2) when the subpopulation of each sample is observed but not chosen, and (3) when the experimenter can select the subpopulation from which each response is sampled. We illustrate the efficiency of the proposed strategy with numerical simulations on synthetic and real data collected from an A/B/n experiment.

Fast Rate Learning in Stochastic First Price Bidding

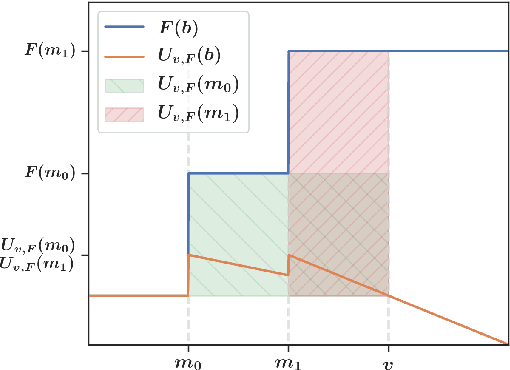
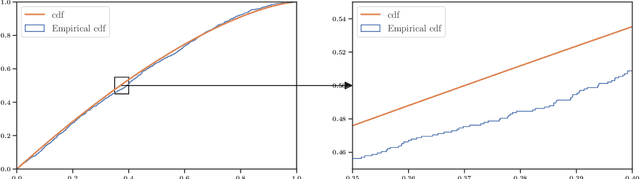
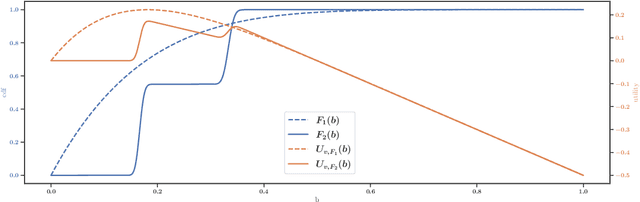
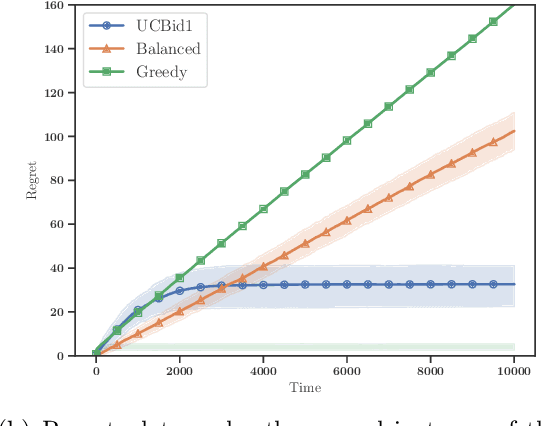
First-price auctions have largely replaced traditional bidding approaches based on Vickrey auctions in programmatic advertising. As far as learning is concerned, first-price auctions are more challenging because the optimal bidding strategy does not only depend on the value of the item but also requires some knowledge of the other bids. They have already given rise to several works in sequential learning, many of which consider models for which the value of the buyer or the opponents' maximal bid is chosen in an adversarial manner. Even in the simplest settings, this gives rise to algorithms whose regret grows as $\sqrt{T}$ with respect to the time horizon $T$. Focusing on the case where the buyer plays against a stationary stochastic environment, we show how to achieve significantly lower regret: when the opponents' maximal bid distribution is known we provide an algorithm whose regret can be as low as $\log^2(T)$; in the case where the distribution must be learnt sequentially, a generalization of this algorithm can achieve $T^{1/3+ \epsilon}$ regret, for any $\epsilon>0$. To obtain these results, we introduce two novel ideas that can be of interest in their own right. First, by transposing results obtained in the posted price setting, we provide conditions under which the first-price biding utility is locally quadratic around its optimum. Second, we leverage the observation that, on small sub-intervals, the concentration of the variations of the empirical distribution function may be controlled more accurately than by using the classical Dvoretzky-Kiefer-Wolfowitz inequality. Numerical simulations confirm that our algorithms converge much faster than alternatives proposed in the literature for various bid distributions, including for bids collected on an actual programmatic advertising platform.

On Limited-Memory Subsampling Strategies for Bandits

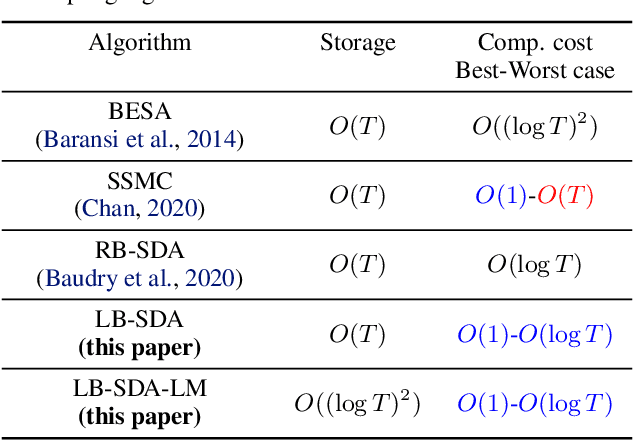
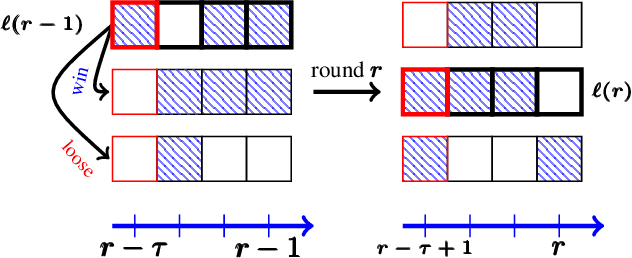
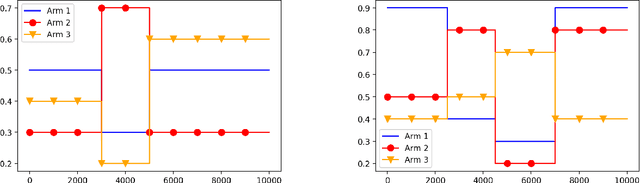
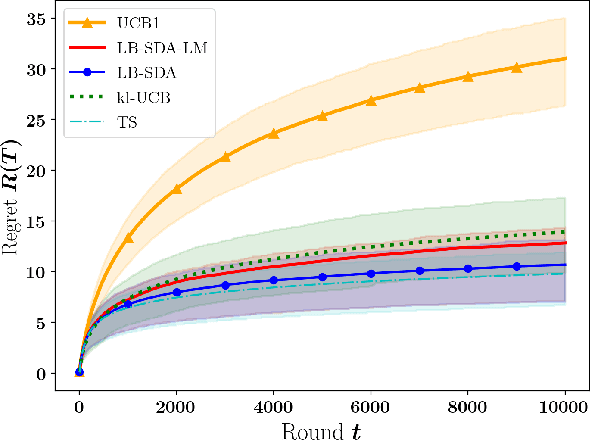
There has been a recent surge of interest in nonparametric bandit algorithms based on subsampling. One drawback however of these approaches is the additional complexity required by random subsampling and the storage of the full history of rewards. Our first contribution is to show that a simple deterministic subsampling rule, proposed in the recent work of Baudry et al. (2020) under the name of ''last-block subsampling'', is asymptotically optimal in one-parameter exponential families. In addition, we prove that these guarantees also hold when limiting the algorithm memory to a polylogarithmic function of the time horizon. These findings open up new perspectives, in particular for non-stationary scenarios in which the arm distributions evolve over time. We propose a variant of the algorithm in which only the most recent observations are used for subsampling, achieving optimal regret guarantees under the assumption of a known number of abrupt changes. Extensive numerical simulations highlight the merits of this approach, particularly when the changes are not only affecting the means of the rewards.

Efficient Algorithms for Stochastic Repeated Second-price Auctions

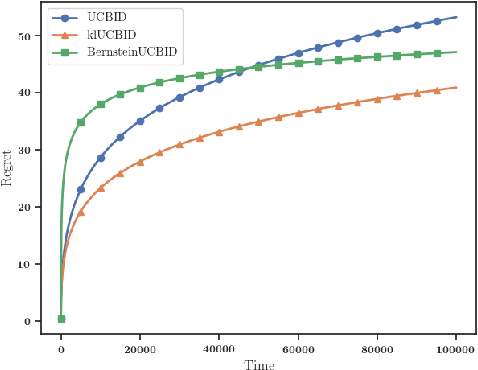
Developing efficient sequential bidding strategies for repeated auctions is an important practical challenge in various marketing tasks. In this setting, the bidding agent obtains information, on both the value of the item at sale and the behavior of the other bidders, only when she wins the auction. Standard bandit theory does not apply to this problem due to the presence of action-dependent censoring. In this work, we consider second-price auctions and propose novel, efficient UCB-like algorithms for this task. These algorithms are analyzed in the stochastic setting, assuming regularity of the distribution of the opponents' bids. We provide regret upper bounds that quantify the improvement over the baseline algorithm proposed in the literature. The improvement is particularly significant in cases when the value of the auctioned item is low, yielding a spectacular reduction in the order of the worst-case regret. We further provide the first parametric lower bound for this problem that applies to generic UCB-like strategies. As an alternative, we propose more explainable strategies which are reminiscent of the Explore Then Commit bandit algorithm. We provide a critical analysis of this class of strategies, showing both important advantages and limitations. In particular, we provide a minimax lower bound and propose a nearly minimax-optimal instance of this class.

Self-Concordant Analysis of Generalized Linear Bandits with Forgetting

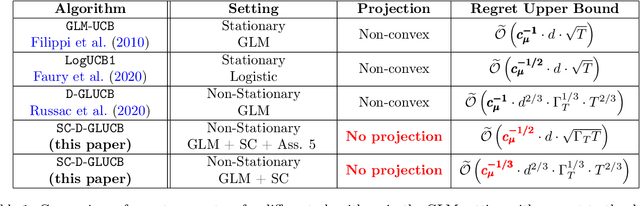
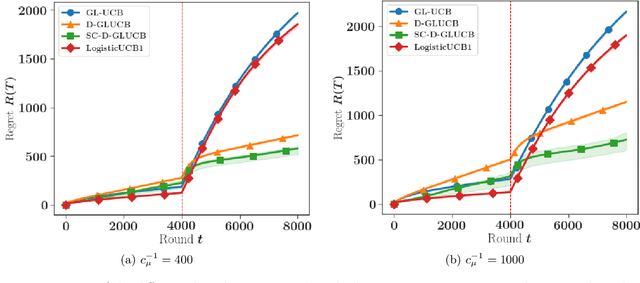
Contextual sequential decision problems with categorical or numerical observations are ubiquitous and Generalized Linear Bandits (GLB) offer a solid theoretical framework to address them. In contrast to the case of linear bandits, existing algorithms for GLB have two drawbacks undermining their applicability. First, they rely on excessively pessimistic concentration bounds due to the non-linear nature of the model. Second, they require either non-convex projection steps or burn-in phases to enforce boundedness of the estimators. Both of these issues are worsened when considering non-stationary models, in which the GLB parameter may vary with time. In this work, we focus on self-concordant GLB (which include logistic and Poisson regression) with forgetting achieved either by the use of a sliding window or exponential weights. We propose a novel confidence-based algorithm for the maximum-likehood estimator with forgetting and analyze its perfomance in abruptly changing environments. These results as well as the accompanying numerical simulations highlight the potential of the proposed approach to address non-stationarity in GLB.