An Optimal Algorithm for Bandit and Zero-Order Convex Optimization with Two-Point Feedback

We consider the closely related problems of bandit convex optimization with two-point feedback, and zero-order stochastic convex optimization with two function evaluations per round. We provide a simple algorithm and analysis which is optimal for convex Lipschitz functions. This improves on \cite{dujww13}, which only provides an optimal result for smooth functions; Moreover, the algorithm and analysis are simpler, and readily extend to non-Euclidean problems. The algorithm is based on a small but surprisingly powerful modification of the gradient estimator.

A Stochastic PCA and SVD Algorithm with an Exponential Convergence Rate

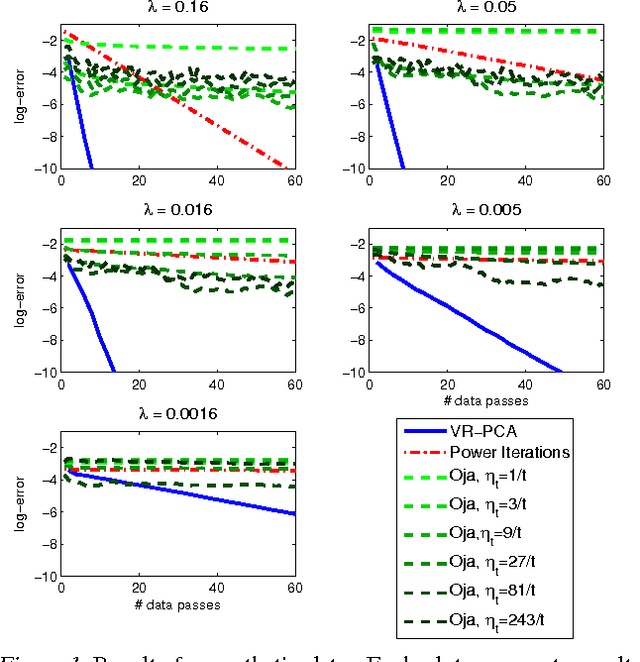
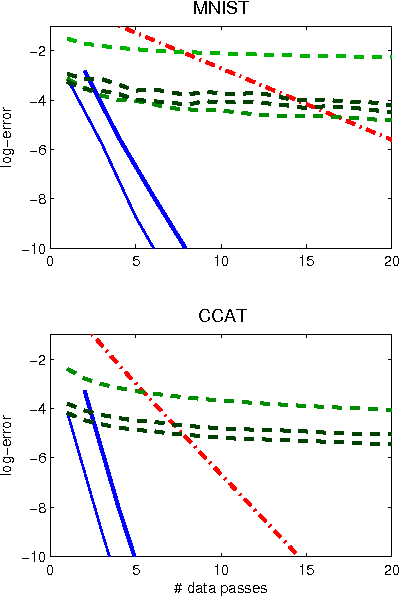
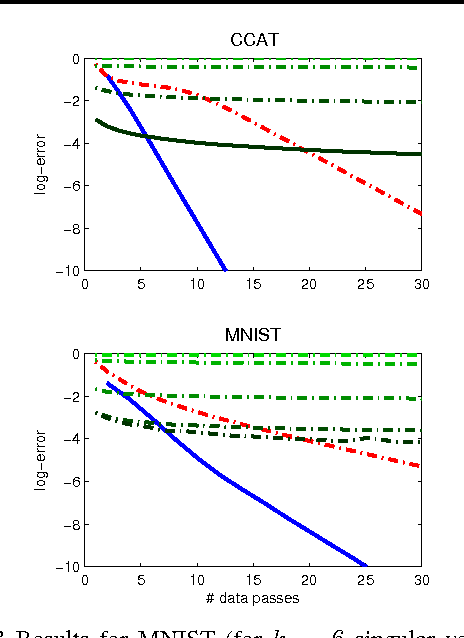
We describe and analyze a simple algorithm for principal component analysis and singular value decomposition, VR-PCA, which uses computationally cheap stochastic iterations, yet converges exponentially fast to the optimal solution. In contrast, existing algorithms suffer either from slow convergence, or computationally intensive iterations whose runtime scales with the data size. The algorithm builds on a recent variance-reduced stochastic gradient technique, which was previously analyzed for strongly convex optimization, whereas here we apply it to an inherently non-convex problem, using a very different analysis.

Learning Exponential Families in High-Dimensions: Strong Convexity and Sparsity

The versatility of exponential families, along with their attendant convexity properties, make them a popular and effective statistical model. A central issue is learning these models in high-dimensions, such as when there is some sparsity pattern of the optimal parameter. This work characterizes a certain strong convexity property of general exponential families, which allow their generalization ability to be quantified. In particular, we show how this property can be used to analyze generic exponential families under L_1 regularization.

On Lower and Upper Bounds for Smooth and Strongly Convex Optimization Problems

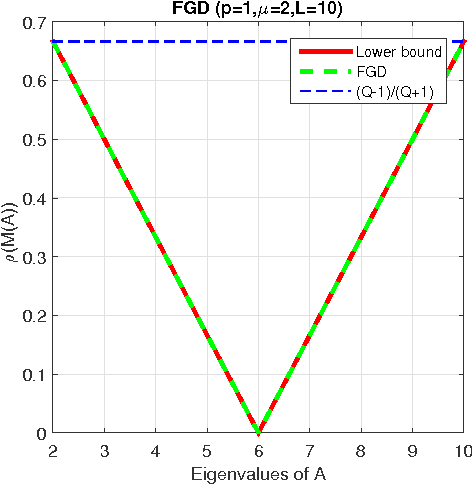
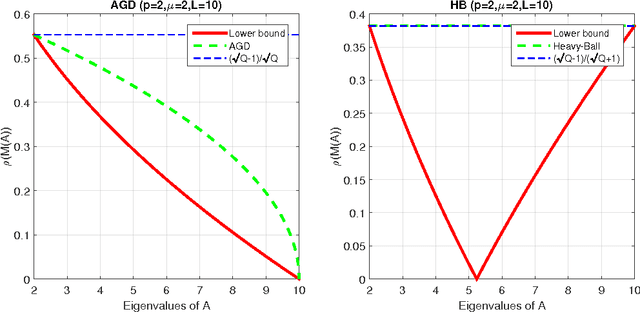
We develop a novel framework to study smooth and strongly convex optimization algorithms, both deterministic and stochastic. Focusing on quadratic functions we are able to examine optimization algorithms as a recursive application of linear operators. This, in turn, reveals a powerful connection between a class of optimization algorithms and the analytic theory of polynomials whereby new lower and upper bounds are derived. Whereas existing lower bounds for this setting are only valid when the dimensionality scales with the number of iterations, our lower bound holds in the natural regime where the dimensionality is fixed. Lastly, expressing it as an optimal solution for the corresponding optimization problem over polynomials, as formulated by our framework, we present a novel systematic derivation of Nesterov's well-known Accelerated Gradient Descent method. This rather natural interpretation of AGD contrasts with earlier ones which lacked a simple, yet solid, motivation.

On the Complexity of Learning with Kernels

A well-recognized limitation of kernel learning is the requirement to handle a kernel matrix, whose size is quadratic in the number of training examples. Many methods have been proposed to reduce this computational cost, mostly by using a subset of the kernel matrix entries, or some form of low-rank matrix approximation, or a random projection method. In this paper, we study lower bounds on the error attainable by such methods as a function of the number of entries observed in the kernel matrix or the rank of an approximate kernel matrix. We show that there are kernel learning problems where no such method will lead to non-trivial computational savings. Our results also quantify how the problem difficulty depends on parameters such as the nature of the loss function, the regularization parameter, the norm of the desired predictor, and the kernel matrix rank. Our results also suggest cases where more efficient kernel learning might be possible.

On the Computational Efficiency of Training Neural Networks

It is well-known that neural networks are computationally hard to train. On the other hand, in practice, modern day neural networks are trained efficiently using SGD and a variety of tricks that include different activation functions (e.g. ReLU), over-specification (i.e., train networks which are larger than needed), and regularization. In this paper we revisit the computational complexity of training neural networks from a modern perspective. We provide both positive and negative results, some of them yield new provably efficient and practical algorithms for training certain types of neural networks.

Fundamental Limits of Online and Distributed Algorithms for Statistical Learning and Estimation

Many machine learning approaches are characterized by information constraints on how they interact with the training data. These include memory and sequential access constraints (e.g. fast first-order methods to solve stochastic optimization problems); communication constraints (e.g. distributed learning); partial access to the underlying data (e.g. missing features and multi-armed bandits) and more. However, currently we have little understanding how such information constraints fundamentally affect our performance, independent of the learning problem semantics. For example, are there learning problems where any algorithm which has small memory footprint (or can use any bounded number of bits from each example, or has certain communication constraints) will perform worse than what is possible without such constraints? In this paper, we describe how a single set of results implies positive answers to the above, for several different settings.

Attribute Efficient Linear Regression with Data-Dependent Sampling

In this paper we analyze a budgeted learning setting, in which the learner can only choose and observe a small subset of the attributes of each training example. We develop efficient algorithms for ridge and lasso linear regression, which utilize the geometry of the data by a novel data-dependent sampling scheme. When the learner has prior knowledge on the second moments of the attributes, the optimal sampling probabilities can be calculated precisely, and result in data-dependent improvements factors for the excess risk over the state-of-the-art that may be as large as $O(\sqrt{d})$, where $d$ is the problem's dimension. Moreover, under reasonable assumptions our algorithms can use less attributes than full-information algorithms, which is the main concern in budgeted learning settings. To the best of our knowledge, these are the first algorithms able to do so in our setting. Where no such prior knowledge is available, we develop a simple estimation technique that given a sufficient amount of training examples, achieves similar improvements. We complement our theoretical analysis with experiments on several data sets which support our claims.

Nonstochastic Multi-Armed Bandits with Graph-Structured Feedback

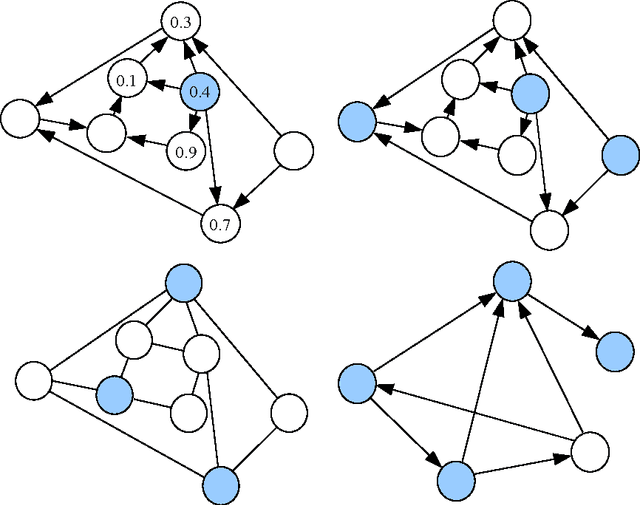
We present and study a partial-information model of online learning, where a decision maker repeatedly chooses from a finite set of actions, and observes some subset of the associated losses. This naturally models several situations where the losses of different actions are related, and knowing the loss of one action provides information on the loss of other actions. Moreover, it generalizes and interpolates between the well studied full-information setting (where all losses are revealed) and the bandit setting (where only the loss of the action chosen by the player is revealed). We provide several algorithms addressing different variants of our setting, and provide tight regret bounds depending on combinatorial properties of the information feedback structure.

On the Complexity of Bandit Linear Optimization

We study the attainable regret for online linear optimization problems with bandit feedback, where unlike the full-information setting, the player can only observe its own loss rather than the full loss vector. We show that the price of bandit information in this setting can be as large as $d$, disproving the well-known conjecture that the regret for bandit linear optimization is at most $\sqrt{d}$ times the full-information regret. Surprisingly, this is shown using "trivial" modifications of standard domains, which have no effect in the full-information setting. This and other results we present highlight some interesting differences between full-information and bandit learning, which were not considered in previous literature.