Do More Negative Samples Necessarily Hurt in Contrastive Learning?

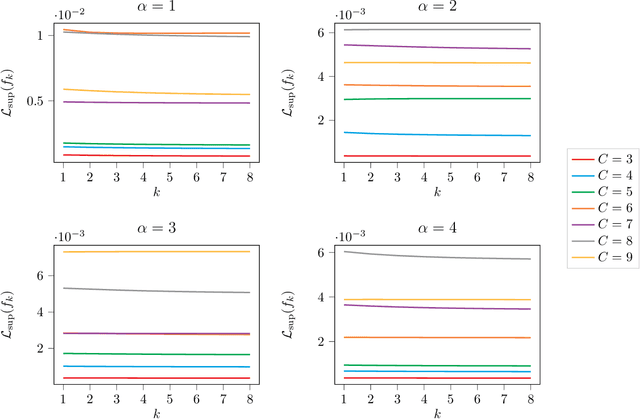
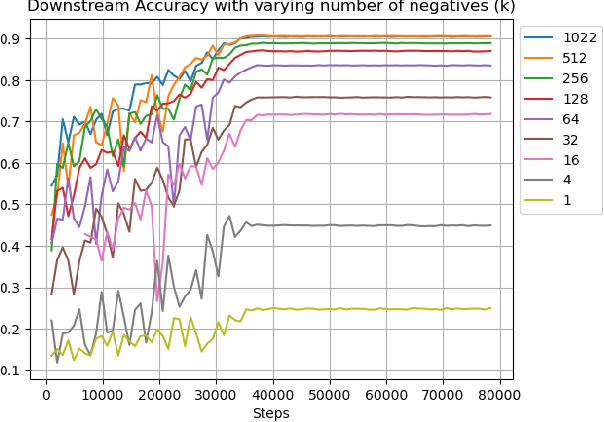
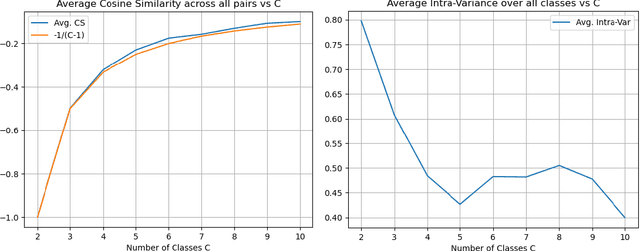
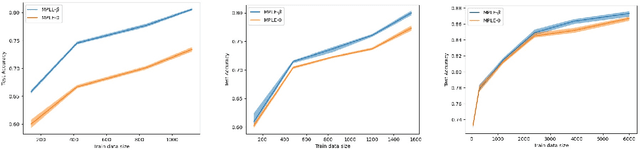
Recent investigations in noise contrastive estimation suggest, both empirically as well as theoretically, that while having more "negative samples" in the contrastive loss improves downstream classification performance initially, beyond a threshold, it hurts downstream performance due to a "collision-coverage" trade-off. But is such a phenomenon inherent in contrastive learning? We show in a simple theoretical setting, where positive pairs are generated by sampling from the underlying latent class (introduced by Saunshi et al. (ICML 2019)), that the downstream performance of the representation optimizing the (population) contrastive loss in fact does not degrade with the number of negative samples. Along the way, we give a structural characterization of the optimal representation in our framework, for noise contrastive estimation. We also provide empirical support for our theoretical results on CIFAR-10 and CIFAR-100 datasets.

Statistical Estimation from Dependent Data

We consider a general statistical estimation problem wherein binary labels across different observations are not independent conditioned on their feature vectors, but dependent, capturing settings where e.g. these observations are collected on a spatial domain, a temporal domain, or a social network, which induce dependencies. We model these dependencies in the language of Markov Random Fields and, importantly, allow these dependencies to be substantial, i.e do not assume that the Markov Random Field capturing these dependencies is in high temperature. As our main contribution we provide algorithms and statistically efficient estimation rates for this model, giving several instantiations of our bounds in logistic regression, sparse logistic regression, and neural network settings with dependent data. Our estimation guarantees follow from novel results for estimating the parameters (i.e. external fields and interaction strengths) of Ising models from a {\em single} sample. {We evaluate our estimation approach on real networked data, showing that it outperforms standard regression approaches that ignore dependencies, across three text classification datasets: Cora, Citeseer and Pubmed.}

For Manifold Learning, Deep Neural Networks can be Locality Sensitive Hash Functions

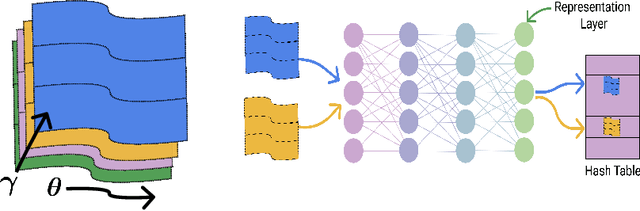
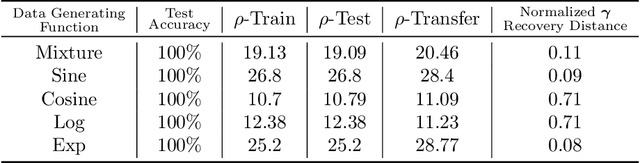
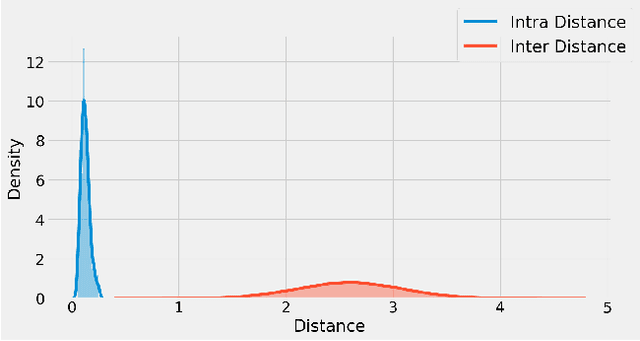
It is well established that training deep neural networks gives useful representations that capture essential features of the inputs. However, these representations are poorly understood in theory and practice. In the context of supervised learning an important question is whether these representations capture features informative for classification, while filtering out non-informative noisy ones. We explore a formalization of this question by considering a generative process where each class is associated with a high-dimensional manifold and different classes define different manifolds. Under this model, each input is produced using two latent vectors: (i) a "manifold identifier" $\gamma$ and; (ii)~a "transformation parameter" $\theta$ that shifts examples along the surface of a manifold. E.g., $\gamma$ might represent a canonical image of a dog, and $\theta$ might stand for variations in pose, background or lighting. We provide theoretical and empirical evidence that neural representations can be viewed as LSH-like functions that map each input to an embedding that is a function of solely the informative $\gamma$ and invariant to $\theta$, effectively recovering the manifold identifier $\gamma$. An important consequence of this behavior is one-shot learning to unseen classes.

Minimax Estimation of Conditional Moment Models

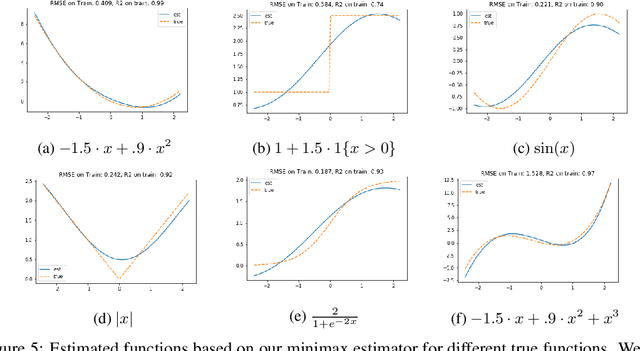
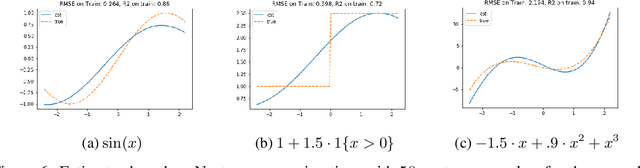
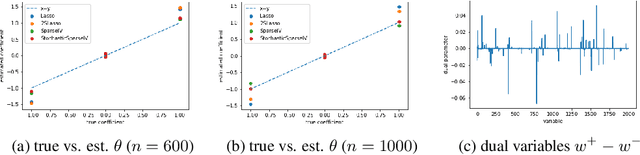
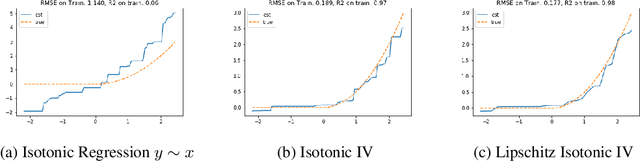
We develop an approach for estimating models described via conditional moment restrictions, with a prototypical application being non-parametric instrumental variable regression. We introduce a min-max criterion function, under which the estimation problem can be thought of as solving a zero-sum game between a modeler who is optimizing over the hypothesis space of the target model and an adversary who identifies violating moments over a test function space. We analyze the statistical estimation rate of the resulting estimator for arbitrary hypothesis spaces, with respect to an appropriate analogue of the mean squared error metric, for ill-posed inverse problems. We show that when the minimax criterion is regularized with a second moment penalty on the test function and the test function space is sufficiently rich, then the estimation rate scales with the critical radius of the hypothesis and test function spaces, a quantity which typically gives tight fast rates. Our main result follows from a novel localized Rademacher analysis of statistical learning problems defined via minimax objectives. We provide applications of our main results for several hypothesis spaces used in practice such as: reproducing kernel Hilbert spaces, high dimensional sparse linear functions, spaces defined via shape constraints, ensemble estimators such as random forests, and neural networks. For each of these applications we provide computationally efficient optimization methods for solving the corresponding minimax problem (e.g. stochastic first-order heuristics for neural networks). In several applications, we show how our modified mean squared error rate, combined with conditions that bound the ill-posedness of the inverse problem, lead to mean squared error rates. We conclude with an extensive experimental analysis of the proposed methods.

Estimating Ising Models from One Sample

Given one sample $X \in \{\pm 1\}^n$ from an Ising model $\Pr[X=x]\propto \exp(x^\top J x/2)$, whose interaction matrix satisfies $J:= \sum_{i=1}^k \beta_i J_i$ for some known matrices $J_i$ and some unknown parameters $\beta_i$, we study whether $J$ can be estimated to high accuracy. Assuming that each node of the Ising model has bounded total interaction with the other nodes, i.e. $\|J\|_{\infty} \le O(1)$, we provide a computationally efficient estimator $\hat{J}$ with the high probability guarantee $\|\hat{J} -J\|_F \le \widetilde O(\sqrt{k})$, where $\|J\|_F$ can be as high as $\Omega(\sqrt{n})$. Our guarantee is tight when the interaction strengths are sufficiently low. An example application of our result is in social networks, wherein nodes make binary choices, $x_1,\ldots,x_n$, which may be influenced at varying strengths $\beta_i$ by different networks $J_i$ in which these nodes belong. By observing a single snapshot of the nodes' behaviors the goal is to learn the combined correlation structure. When $k=1$ and a single parameter is to be inferred, we further show $|\hat{\beta}_1 - \beta_1| \le \widetilde O(F(\beta_1J_1)^{-1/2})$, where $F(\beta_1J_1)$ is the log-partition function of the model. This was proved in prior work under additional assumptions. We generalize these results to any setting. While our guarantees aim both high and low temperature regimes, our proof relies on sparsifying the correlation network by conditioning on subsets of the variables, such that the unconditioned variables satisfy Dobrushin's condition, i.e. a high temperature condition which allows us to apply stronger concentration inequalities. We use this to prove concentration and anti-concentration properties of the Ising model, and we believe this sparsification result has applications beyond the scope of this paper as well.

Logistic-Regression with peer-group effects via inference in higher order Ising models

Spin glass models, such as the Sherrington-Kirkpatrick, Hopfield and Ising models, are all well-studied members of the exponential family of discrete distributions, and have been influential in a number of application domains where they are used to model correlation phenomena on networks. Conventionally these models have quadratic sufficient statistics and consequently capture correlations arising from pairwise interactions. In this work we study extensions of these to models with higher-order sufficient statistics, modeling behavior on a social network with peer-group effects. In particular, we model binary outcomes on a network as a higher-order spin glass, where the behavior of an individual depends on a linear function of their own vector of covariates and some polynomial function of the behavior of others, capturing peer-group effects. Using a {\em single}, high-dimensional sample from such model our goal is to recover the coefficients of the linear function as well as the strength of the peer-group effects. The heart of our result is a novel approach for showing strong concavity of the log pseudo-likelihood of the model, implying statistical error rate of $\sqrt{d/n}$ for the Maximum Pseudo-Likelihood Estimator (MPLE), where $d$ is the dimensionality of the covariate vectors and $n$ is the size of the network (number of nodes). Our model generalizes vanilla logistic regression as well as the peer-effect models studied in recent works, and our results extend these results to accommodate higher-order interactions.

Learning from weakly dependent data under Dobrushin's condition

Statistical learning theory has largely focused on learning and generalization given independent and identically distributed (i.i.d.) samples. Motivated by applications involving time-series data, there has been a growing literature on learning and generalization in settings where data is sampled from an ergodic process. This work has also developed complexity measures, which appropriately extend the notion of Rademacher complexity to bound the generalization error and learning rates of hypothesis classes in this setting. Rather than time-series data, our work is motivated by settings where data is sampled on a network or a spatial domain, and thus do not fit well within the framework of prior work. We provide learning and generalization bounds for data that are complexly dependent, yet their distribution satisfies the standard Dobrushin's condition. Indeed, we show that the standard complexity measures of Gaussian and Rademacher complexities and VC dimension are sufficient measures of complexity for the purposes of bounding the generalization error and learning rates of hypothesis classes in our setting. Moreover, our generalization bounds only degrade by constant factors compared to their i.i.d. analogs, and our learnability bounds degrade by log factors in the size of the training set.

Regression from Dependent Observations

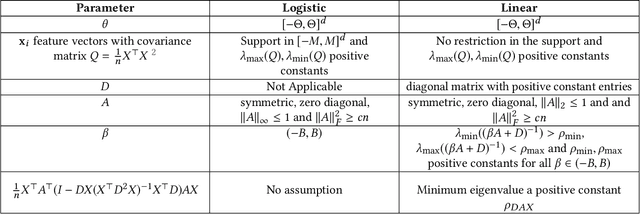
The standard linear and logistic regression models assume that the response variables are independent, but share the same linear relationship to their corresponding vectors of covariates. The assumption that the response variables are independent is, however, too strong. In many applications, these responses are collected on nodes of a network, or some spatial or temporal domain, and are dependent. Examples abound in financial and meteorological applications, and dependencies naturally arise in social networks through peer effects. Regression with dependent responses has thus received a lot of attention in the Statistics and Economics literature, but there are no strong consistency results unless multiple independent samples of the vectors of dependent responses can be collected from these models. We present computationally and statistically efficient methods for linear and logistic regression models when the response variables are dependent on a network. Given one sample from a networked linear or logistic regression model and under mild assumptions, we prove strong consistency results for recovering the vector of coefficients and the strength of the dependencies, recovering the rates of standard regression under independent observations. We use projected gradient descent on the negative log-likelihood, or negative log-pseudolikelihood, and establish their strong convexity and consistency using concentration of measure for dependent random variables.

HOGWILD!-Gibbs can be PanAccurate

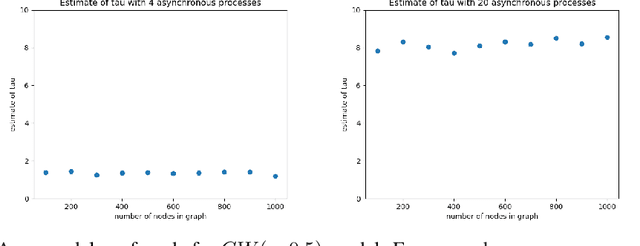
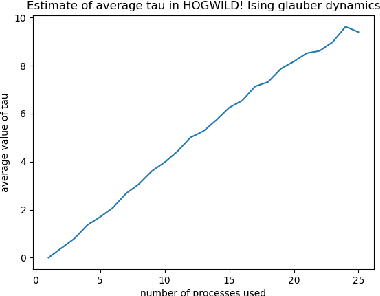
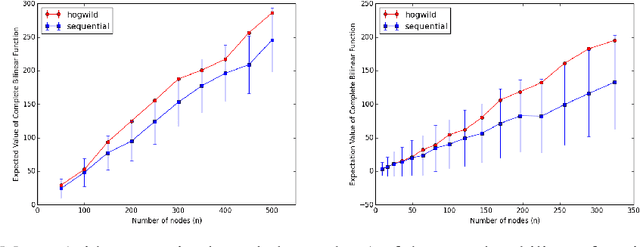
Asynchronous Gibbs sampling has been recently shown to be fast-mixing and an accurate method for estimating probabilities of events on a small number of variables of a graphical model satisfying Dobrushin's condition~\cite{DeSaOR16}. We investigate whether it can be used to accurately estimate expectations of functions of {\em all the variables} of the model. Under the same condition, we show that the synchronous (sequential) and asynchronous Gibbs samplers can be coupled so that the expected Hamming distance between their (multivariate) samples remains bounded by $O(\tau \log n),$ where $n$ is the number of variables in the graphical model, and $\tau$ is a measure of the asynchronicity. A similar bound holds for any constant power of the Hamming distance. Hence, the expectation of any function that is Lipschitz with respect to a power of the Hamming distance, can be estimated with a bias that grows logarithmically in $n$. Going beyond Lipschitz functions, we consider the bias arising from asynchronicity in estimating the expectation of polynomial functions of all variables in the model. Using recent concentration of measure results, we show that the bias introduced by the asynchronicity is of smaller order than the standard deviation of the function value already present in the true model. We perform experiments on a multi-processor machine to empirically illustrate our theoretical findings.

From Soft Classifiers to Hard Decisions: How fair can we be?

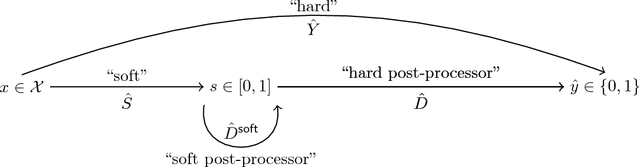
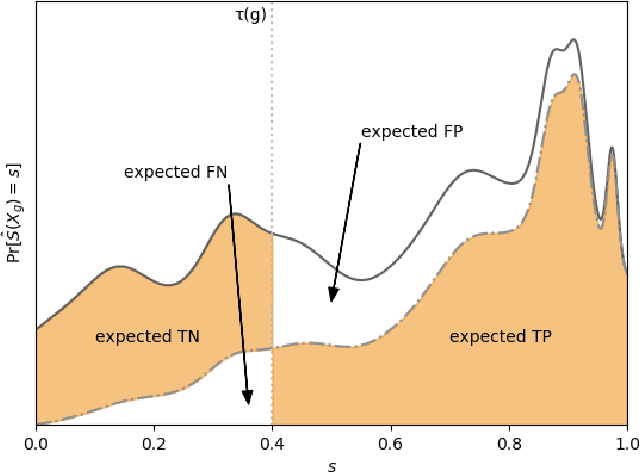
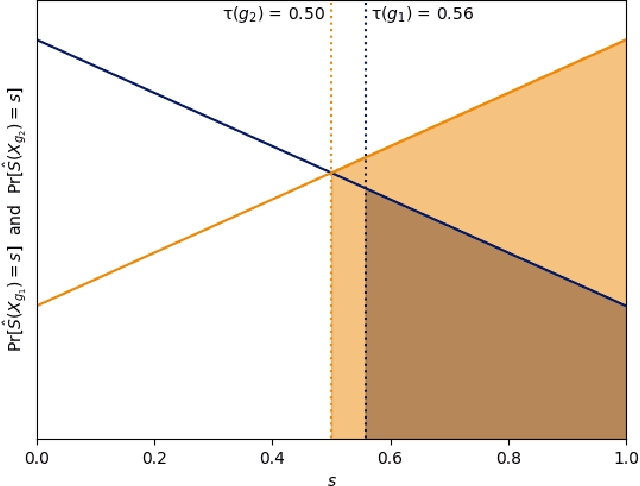
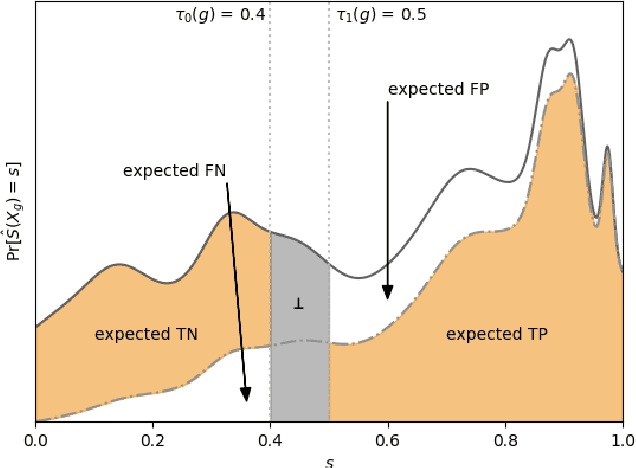
A popular methodology for building binary decision-making classifiers in the presence of imperfect information is to first construct a non-binary "scoring" classifier that is calibrated over all protected groups, and then to post-process this score to obtain a binary decision. We study the feasibility of achieving various fairness properties by post-processing calibrated scores, and then show that deferring post-processors allow for more fairness conditions to hold on the final decision. Specifically, we show: 1. There does not exist a general way to post-process a calibrated classifier to equalize protected groups' positive or negative predictive value (PPV or NPV). For certain "nice" calibrated classifiers, either PPV or NPV can be equalized when the post-processor uses different thresholds across protected groups, though there exist distributions of calibrated scores for which the two measures cannot be both equalized. When the post-processing consists of a single global threshold across all groups, natural fairness properties, such as equalizing PPV in a nontrivial way, do not hold even for "nice" classifiers. 2. When the post-processing is allowed to `defer' on some decisions (that is, to avoid making a decision by handing off some examples to a separate process), then for the non-deferred decisions, the resulting classifier can be made to equalize PPV, NPV, false positive rate (FPR) and false negative rate (FNR) across the protected groups. This suggests a way to partially evade the impossibility results of Chouldechova and Kleinberg et al., which preclude equalizing all of these measures simultaneously. We also present different deferring strategies and show how they affect the fairness properties of the overall system. We evaluate our post-processing techniques using the COMPAS data set from 2016.