Siddhartha Jayanti
Learning from weakly dependent data under Dobrushin's condition
Jun 21, 2019Abstract:Statistical learning theory has largely focused on learning and generalization given independent and identically distributed (i.i.d.) samples. Motivated by applications involving time-series data, there has been a growing literature on learning and generalization in settings where data is sampled from an ergodic process. This work has also developed complexity measures, which appropriately extend the notion of Rademacher complexity to bound the generalization error and learning rates of hypothesis classes in this setting. Rather than time-series data, our work is motivated by settings where data is sampled on a network or a spatial domain, and thus do not fit well within the framework of prior work. We provide learning and generalization bounds for data that are complexly dependent, yet their distribution satisfies the standard Dobrushin's condition. Indeed, we show that the standard complexity measures of Gaussian and Rademacher complexities and VC dimension are sufficient measures of complexity for the purposes of bounding the generalization error and learning rates of hypothesis classes in our setting. Moreover, our generalization bounds only degrade by constant factors compared to their i.i.d. analogs, and our learnability bounds degrade by log factors in the size of the training set.
HOGWILD!-Gibbs can be PanAccurate
Nov 26, 2018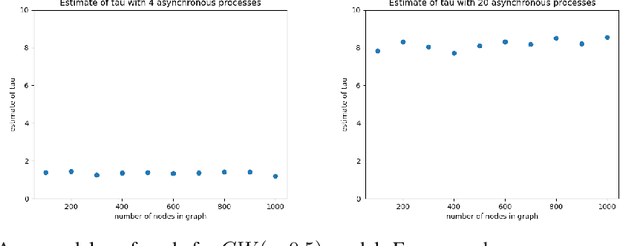
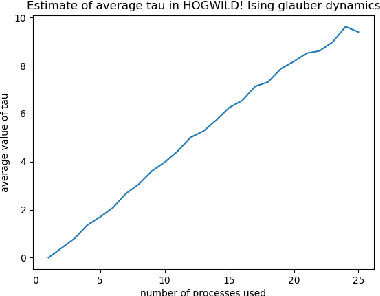
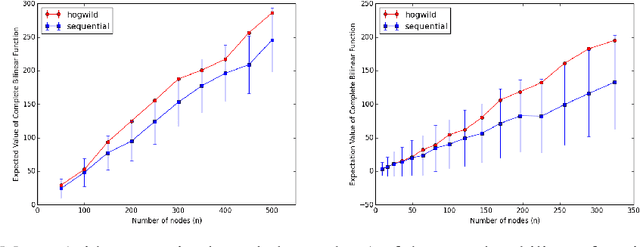
Abstract:Asynchronous Gibbs sampling has been recently shown to be fast-mixing and an accurate method for estimating probabilities of events on a small number of variables of a graphical model satisfying Dobrushin's condition~\cite{DeSaOR16}. We investigate whether it can be used to accurately estimate expectations of functions of {\em all the variables} of the model. Under the same condition, we show that the synchronous (sequential) and asynchronous Gibbs samplers can be coupled so that the expected Hamming distance between their (multivariate) samples remains bounded by $O(\tau \log n),$ where $n$ is the number of variables in the graphical model, and $\tau$ is a measure of the asynchronicity. A similar bound holds for any constant power of the Hamming distance. Hence, the expectation of any function that is Lipschitz with respect to a power of the Hamming distance, can be estimated with a bias that grows logarithmically in $n$. Going beyond Lipschitz functions, we consider the bias arising from asynchronicity in estimating the expectation of polynomial functions of all variables in the model. Using recent concentration of measure results, we show that the bias introduced by the asynchronicity is of smaller order than the standard deviation of the function value already present in the true model. We perform experiments on a multi-processor machine to empirically illustrate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge