Fast Fusion of Multi-Band Images Based on Solving a Sylvester Equation

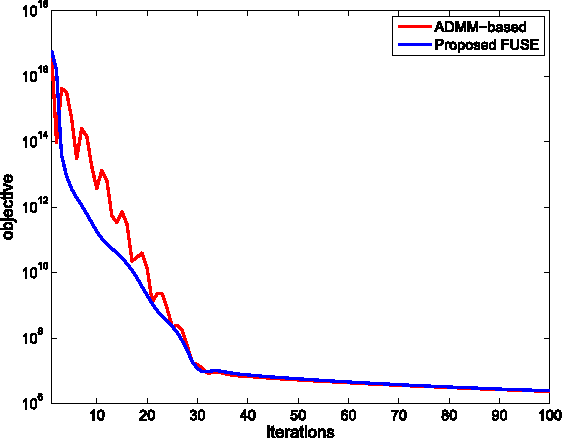
This paper proposes a fast multi-band image fusion algorithm, which combines a high-spatial low-spectral resolution image and a low-spatial high-spectral resolution image. The well admitted forward model is explored to form the likelihoods of the observations. Maximizing the likelihoods leads to solving a Sylvester equation. By exploiting the properties of the circulant and downsampling matrices associated with the fusion problem, a closed-form solution for the corresponding Sylvester equation is obtained explicitly, getting rid of any iterative update step. Coupled with the alternating direction method of multipliers and the block coordinate descent method, the proposed algorithm can be easily generalized to incorporate prior information for the fusion problem, allowing a Bayesian estimator. Simulation results show that the proposed algorithm achieves the same performance as existing algorithms with the advantage of significantly decreasing the computational complexity of these algorithms.

Hyperspectral and Multispectral Image Fusion based on a Sparse Representation

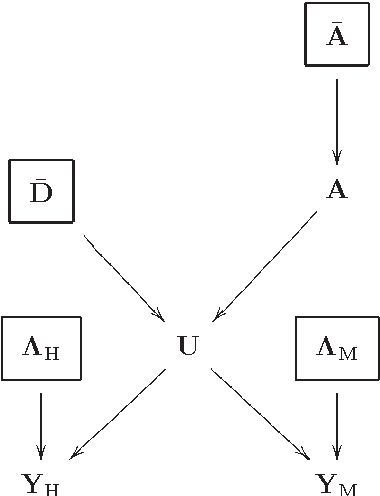
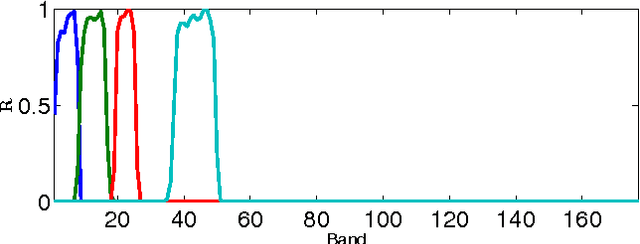
This paper presents a variational based approach to fusing hyperspectral and multispectral images. The fusion process is formulated as an inverse problem whose solution is the target image assumed to live in a much lower dimensional subspace. A sparse regularization term is carefully designed, relying on a decomposition of the scene on a set of dictionaries. The dictionary atoms and the corresponding supports of active coding coefficients are learned from the observed images. Then, conditionally on these dictionaries and supports, the fusion problem is solved via alternating optimization with respect to the target image (using the alternating direction method of multipliers) and the coding coefficients. Simulation results demonstrate the efficiency of the proposed algorithm when compared with the state-of-the-art fusion methods.

Bayesian Fusion of Multi-Band Images

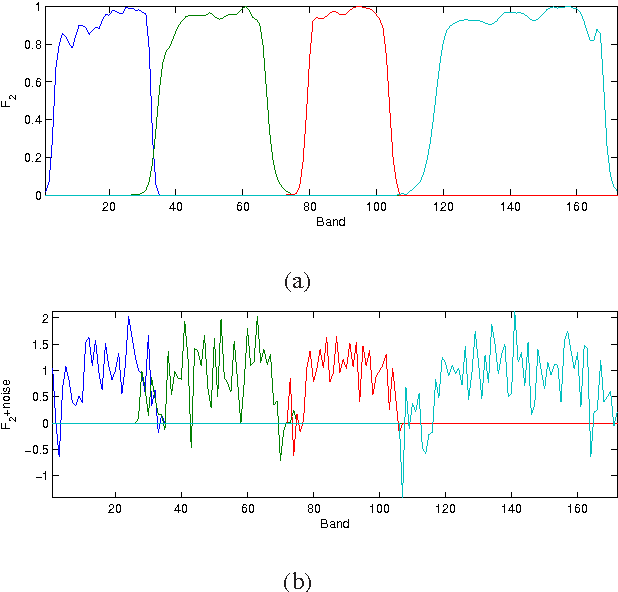
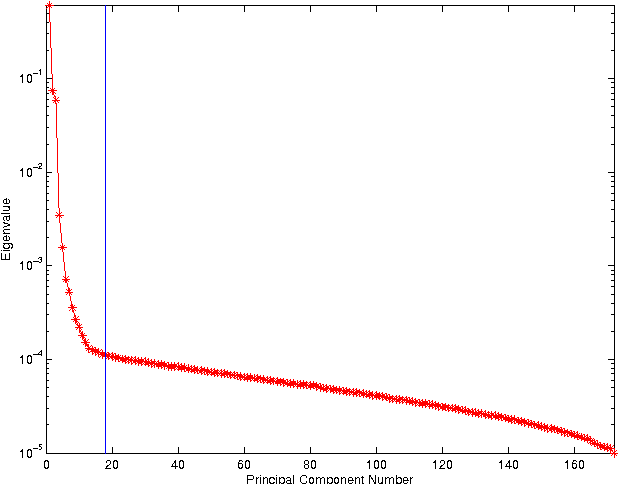
In this paper, a Bayesian fusion technique for remotely sensed multi-band images is presented. The observed images are related to the high spectral and high spatial resolution image to be recovered through physical degradations, e.g., spatial and spectral blurring and/or subsampling defined by the sensor characteristics. The fusion problem is formulated within a Bayesian estimation framework. An appropriate prior distribution exploiting geometrical consideration is introduced. To compute the Bayesian estimator of the scene of interest from its posterior distribution, a Markov chain Monte Carlo algorithm is designed to generate samples asymptotically distributed according to the target distribution. To efficiently sample from this high-dimension distribution, a Hamiltonian Monte Carlo step is introduced in the Gibbs sampling strategy. The efficiency of the proposed fusion method is evaluated with respect to several state-of-the-art fusion techniques. In particular, low spatial resolution hyperspectral and multispectral images are fused to produce a high spatial resolution hyperspectral image.

Nonlinear hyperspectral unmixing with robust nonnegative matrix factorization

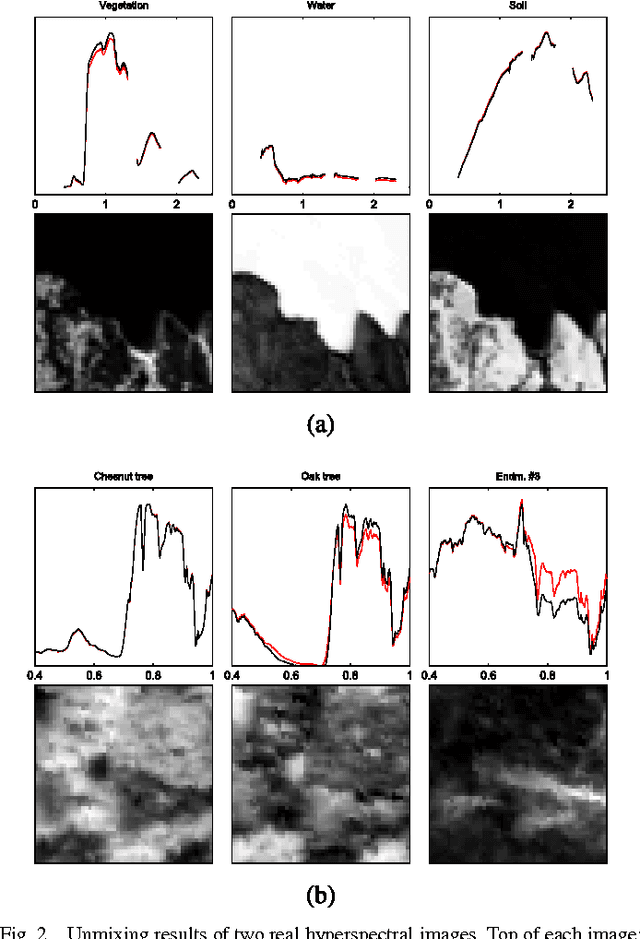
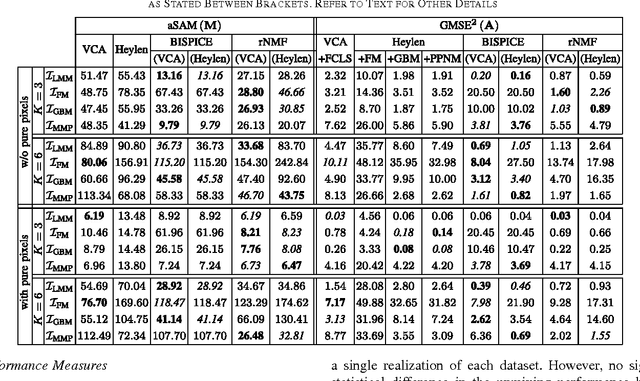
This paper introduces a robust mixing model to describe hyperspectral data resulting from the mixture of several pure spectral signatures. This new model not only generalizes the commonly used linear mixing model, but also allows for possible nonlinear effects to be easily handled, relying on mild assumptions regarding these nonlinearities. The standard nonnegativity and sum-to-one constraints inherent to spectral unmixing are coupled with a group-sparse constraint imposed on the nonlinearity component. This results in a new form of robust nonnegative matrix factorization. The data fidelity term is expressed as a beta-divergence, a continuous family of dissimilarity measures that takes the squared Euclidean distance and the generalized Kullback-Leibler divergence as special cases. The penalized objective is minimized with a block-coordinate descent that involves majorization-minimization updates. Simulation results obtained on synthetic and real data show that the proposed strategy competes with state-of-the-art linear and nonlinear unmixing methods.

Joint Bayesian estimation of close subspaces from noisy measurements

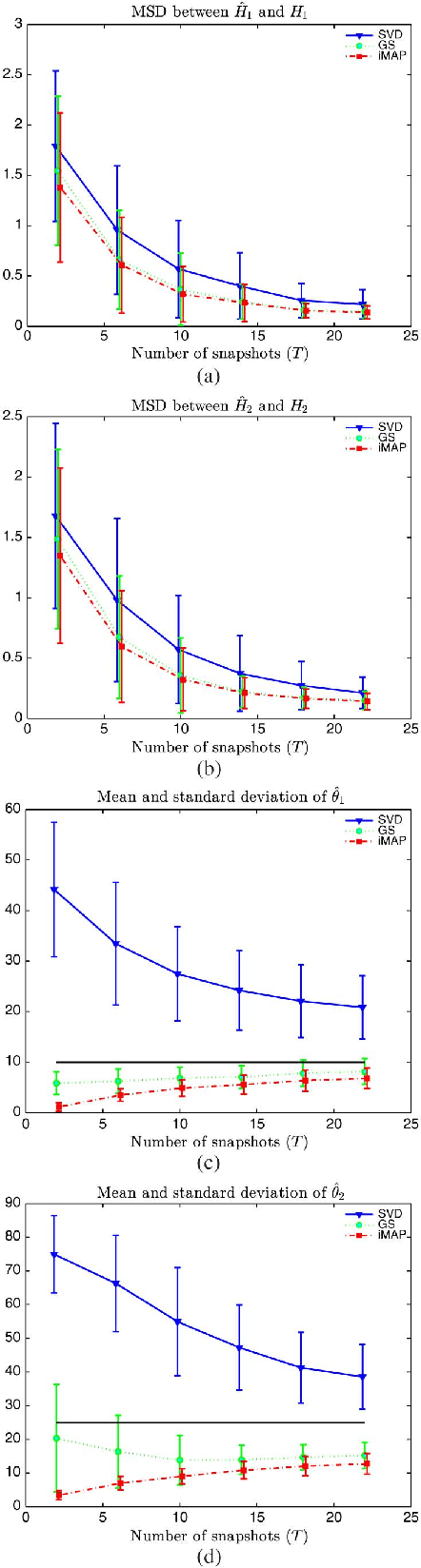
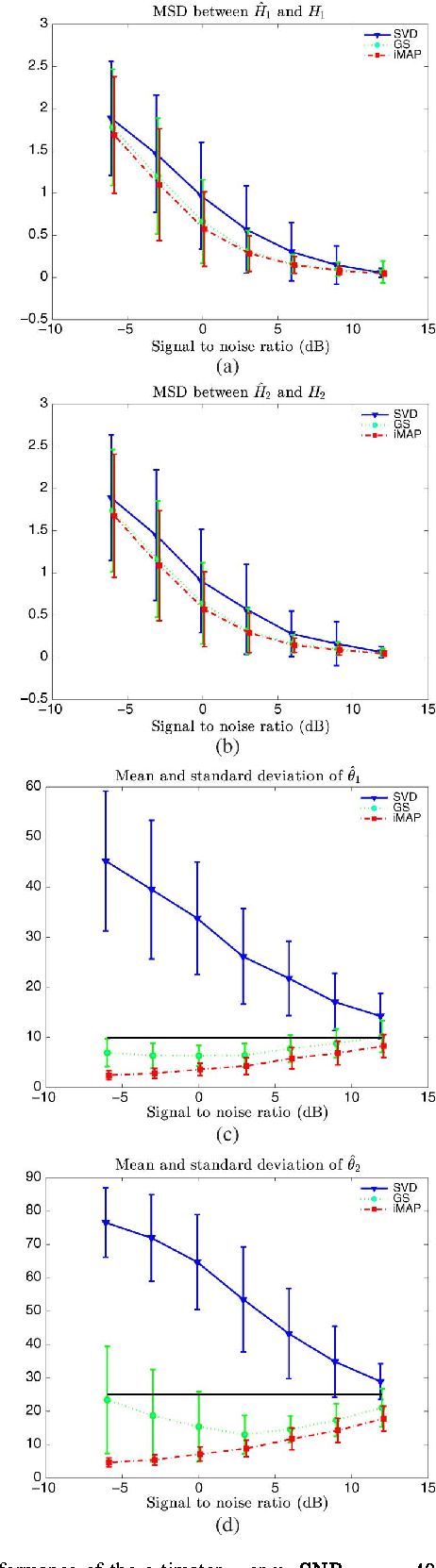
In this letter, we consider two sets of observations defined as subspace signals embedded in noise and we wish to analyze the distance between these two subspaces. The latter entails evaluating the angles between the subspaces, an issue reminiscent of the well-known Procrustes problem. A Bayesian approach is investigated where the subspaces of interest are considered as random with a joint prior distribution (namely a Bingham distribution), which allows the closeness of the two subspaces to be adjusted. Within this framework, the minimum mean-square distance estimator of both subspaces is formulated and implemented via a Gibbs sampler. A simpler scheme based on alternative maximum a posteriori estimation is also presented. The new schemes are shown to provide more accurate estimates of the angles between the subspaces, compared to singular value decomposition based independent estimation of the two subspaces.

Nonlinear unmixing of hyperspectral images: models and algorithms

When considering the problem of unmixing hyperspectral images, most of the literature in the geoscience and image processing areas relies on the widely used linear mixing model (LMM). However, the LMM may be not valid and other nonlinear models need to be considered, for instance, when there are multi-scattering effects or intimate interactions. Consequently, over the last few years, several significant contributions have been proposed to overcome the limitations inherent in the LMM. In this paper, we present an overview of recent advances in nonlinear unmixing modeling.

Variational Semi-blind Sparse Deconvolution with Orthogonal Kernel Bases and its Application to MRFM

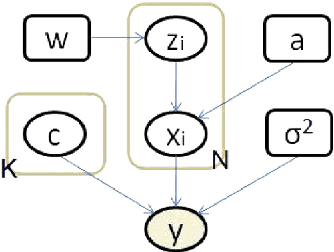
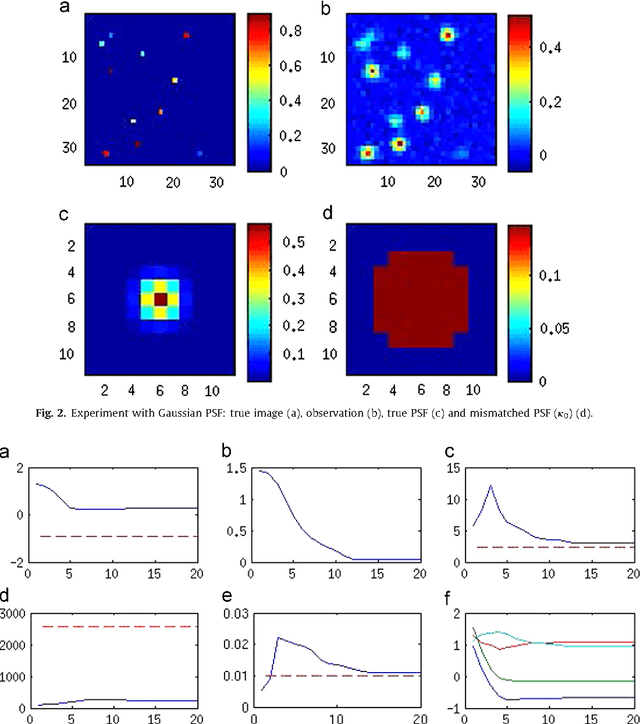
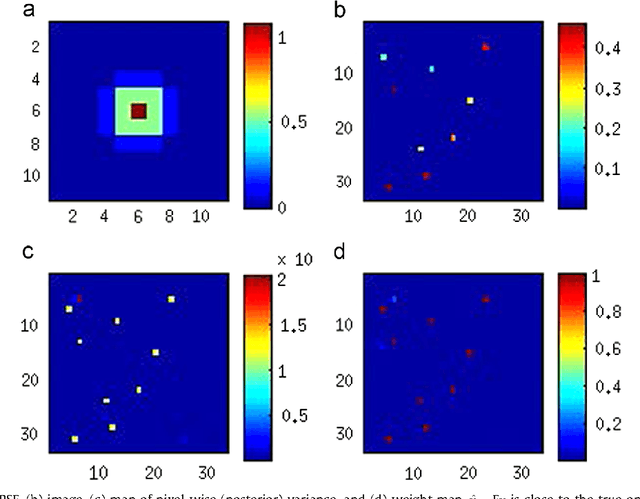
We present a variational Bayesian method of joint image reconstruction and point spread function (PSF) estimation when the PSF of the imaging device is only partially known. To solve this semi-blind deconvolution problem, prior distributions are specified for the PSF and the 3D image. Joint image reconstruction and PSF estimation is then performed within a Bayesian framework, using a variational algorithm to estimate the posterior distribution. The image prior distribution imposes an explicit atomic measure that corresponds to image sparsity. Importantly, the proposed Bayesian deconvolution algorithm does not require hand tuning. Simulation results clearly demonstrate that the semi-blind deconvolution algorithm compares favorably with previous Markov chain Monte Carlo (MCMC) version of myopic sparse reconstruction. It significantly outperforms mismatched non-blind algorithms that rely on the assumption of the perfect knowledge of the PSF. The algorithm is illustrated on real data from magnetic resonance force microscopy (MRFM).

Nonlinear spectral unmixing of hyperspectral images using Gaussian processes

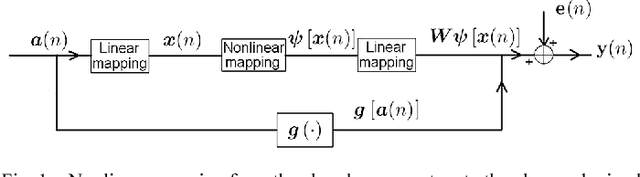
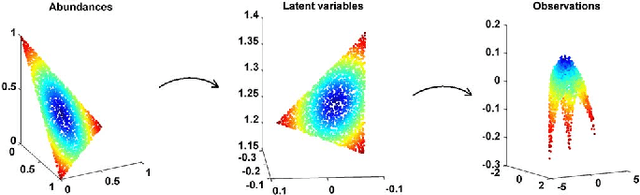
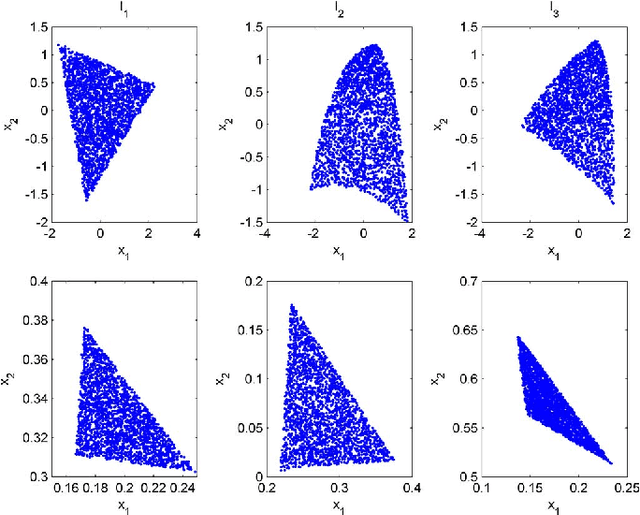
This paper presents an unsupervised algorithm for nonlinear unmixing of hyperspectral images. The proposed model assumes that the pixel reflectances result from a nonlinear function of the abundance vectors associated with the pure spectral components. We assume that the spectral signatures of the pure components and the nonlinear function are unknown. The first step of the proposed method consists of the Bayesian estimation of the abundance vectors for all the image pixels and the nonlinear function relating the abundance vectors to the observations. The endmembers are subsequently estimated using Gaussian process regression. The performance of the unmixing strategy is evaluated with simulations conducted on synthetic and real data.

Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches

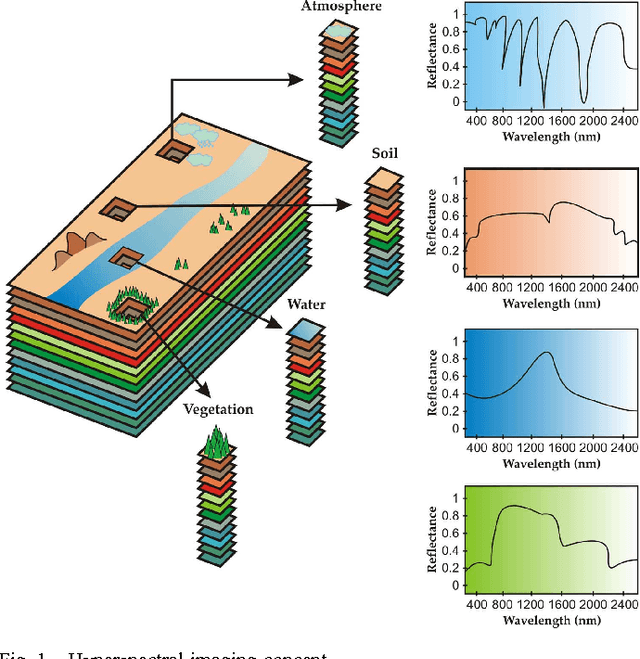
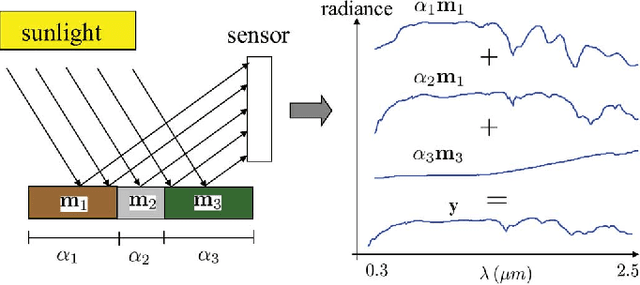
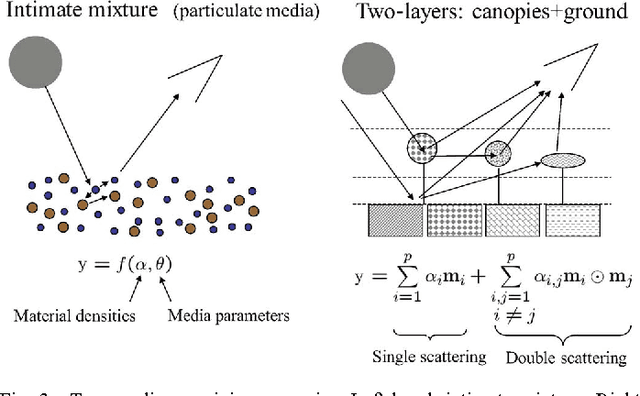
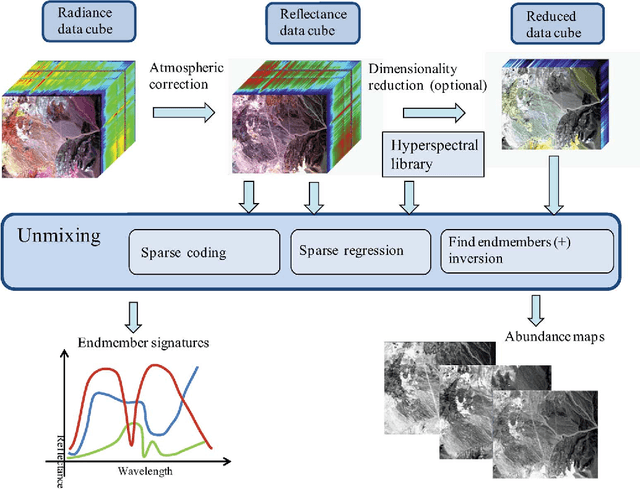
Imaging spectrometers measure electromagnetic energy scattered in their instantaneous field view in hundreds or thousands of spectral channels with higher spectral resolution than multispectral cameras. Imaging spectrometers are therefore often referred to as hyperspectral cameras (HSCs). Higher spectral resolution enables material identification via spectroscopic analysis, which facilitates countless applications that require identifying materials in scenarios unsuitable for classical spectroscopic analysis. Due to low spatial resolution of HSCs, microscopic material mixing, and multiple scattering, spectra measured by HSCs are mixtures of spectra of materials in a scene. Thus, accurate estimation requires unmixing. Pixels are assumed to be mixtures of a few materials, called endmembers. Unmixing involves estimating all or some of: the number of endmembers, their spectral signatures, and their abundances at each pixel. Unmixing is a challenging, ill-posed inverse problem because of model inaccuracies, observation noise, environmental conditions, endmember variability, and data set size. Researchers have devised and investigated many models searching for robust, stable, tractable, and accurate unmixing algorithms. This paper presents an overview of unmixing methods from the time of Keshava and Mustard's unmixing tutorial [1] to the present. Mixing models are first discussed. Signal-subspace, geometrical, statistical, sparsity-based, and spatial-contextual unmixing algorithms are described. Mathematical problems and potential solutions are described. Algorithm characteristics are illustrated experimentally.

Semi-blind Sparse Image Reconstruction with Application to MRFM

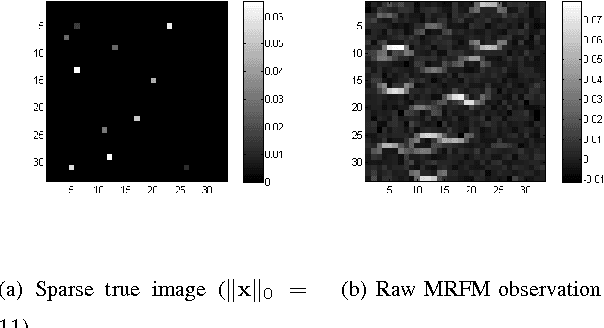
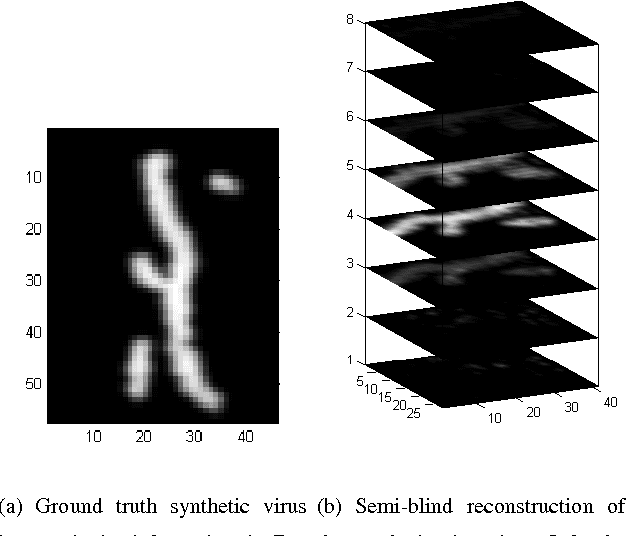
We propose a solution to the image deconvolution problem where the convolution kernel or point spread function (PSF) is assumed to be only partially known. Small perturbations generated from the model are exploited to produce a few principal components explaining the PSF uncertainty in a high dimensional space. Unlike recent developments on blind deconvolution of natural images, we assume the image is sparse in the pixel basis, a natural sparsity arising in magnetic resonance force microscopy (MRFM). Our approach adopts a Bayesian Metropolis-within-Gibbs sampling framework. The performance of our Bayesian semi-blind algorithm for sparse images is superior to previously proposed semi-blind algorithms such as the alternating minimization (AM) algorithm and blind algorithms developed for natural images. We illustrate our myopic algorithm on real MRFM tobacco virus data.