Partially adaptive filtering using randomized projections

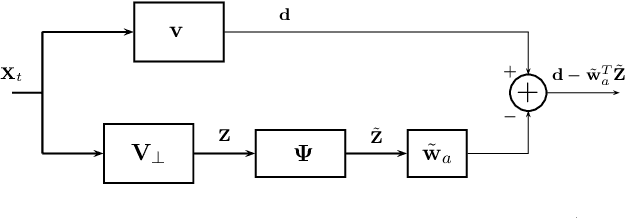
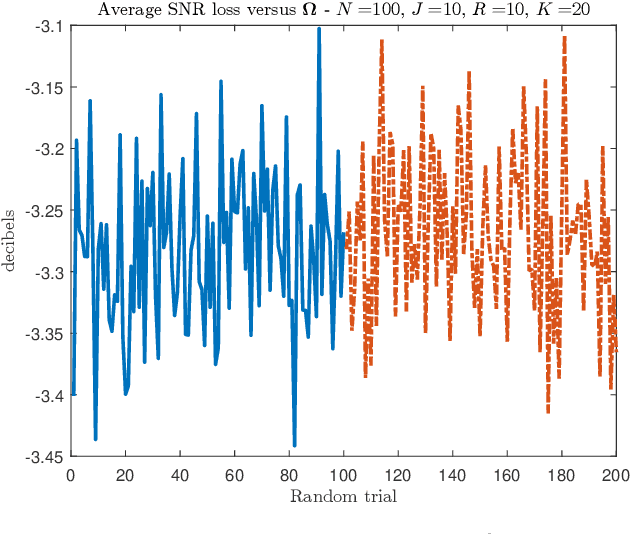
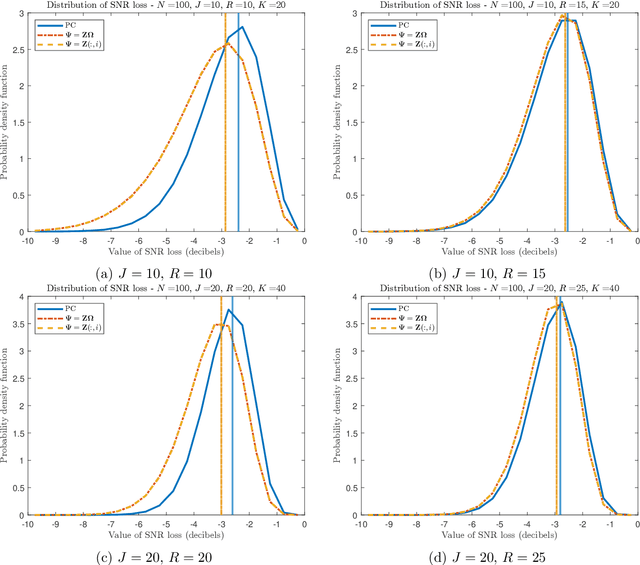
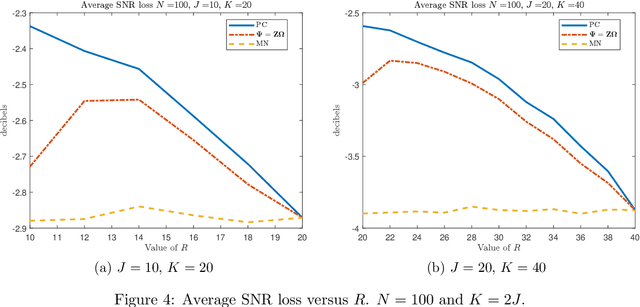
This short note addresses the design of a partially adaptive filter to retrieve a signal of interest in the presence of strong low-rank interference and thermal noise. We consider a generalized sidelobe canceler implementation where the dimension-reducing transformation is build resorting to ideas borrowed from randomized matrix approximations. More precisely, the main subspace of the auxiliary data $Z$ is approximated by $Z\Omega$ where $\Omega$ is a random matrix or a matrix that picks at random columns of $Z$. These transformations do not require eigenvalue decomposition, yet they provide performance similar to those of a principal component filter.

A short overview of adaptive multichannel filters SNR loss analysis

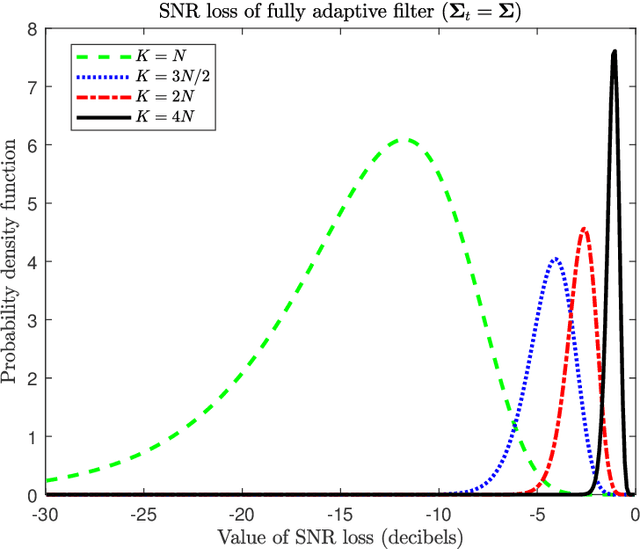
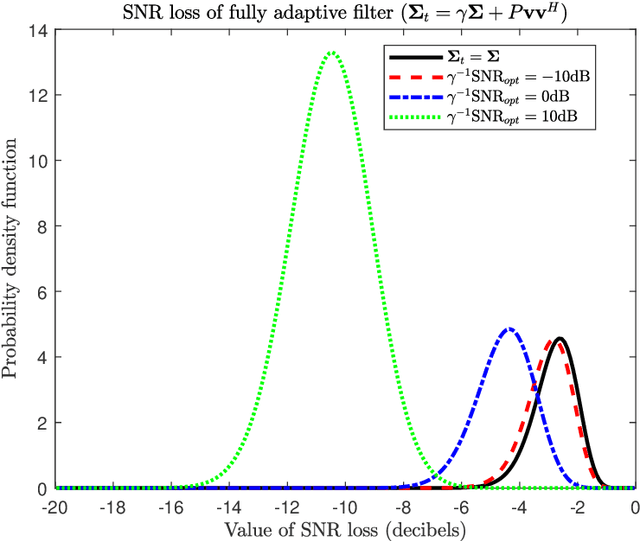
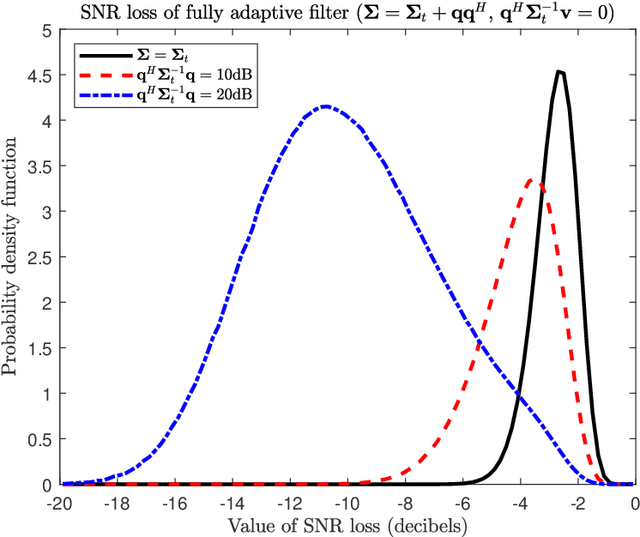
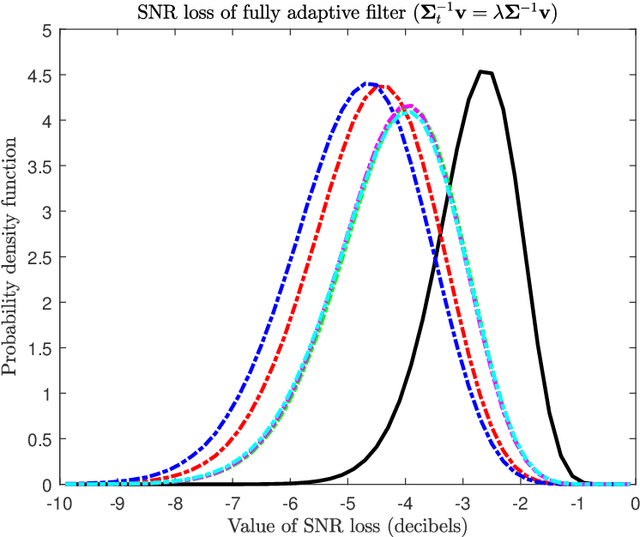
Many multichannel systems use a linear filter to retrieve a signal of interest corrupted by noise whose statistics are partly unknown. The optimal filter in Gaussian noise requires knowledge of the noise covariance matrix $\Sigma$ and in practice the latter is estimated from a set of training samples. An important issue concerns the characterization of the performance of such adaptive filters. This is generally achieved using as figure of merit the ratio of the signal to noise ratio (SNR) at the output of the adaptive filter to the SNR obtained with the clairvoyant -- known $\Sigma$ -- filter. This problem has been studied extensively since the seventies and this document presents a concise overview of results published in the literature. We consider various cases about the training samples covariance matrix and we investigate fully adaptive, partially adaptive and regularized filters.

On the distributions of some statistics related to adaptive filters trained with $t$-distributed samples

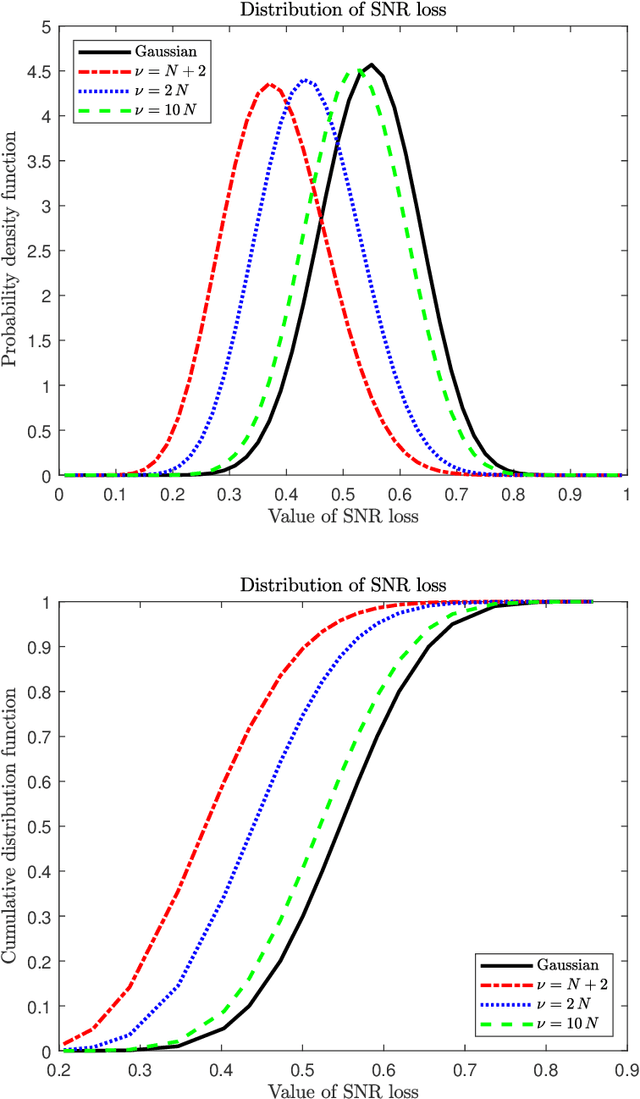
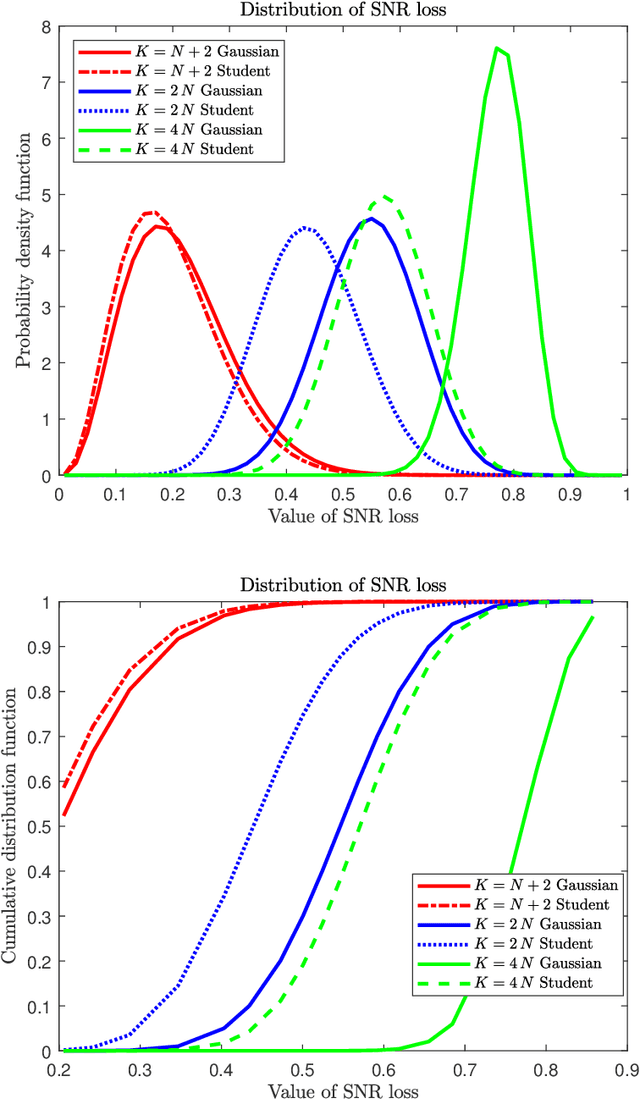
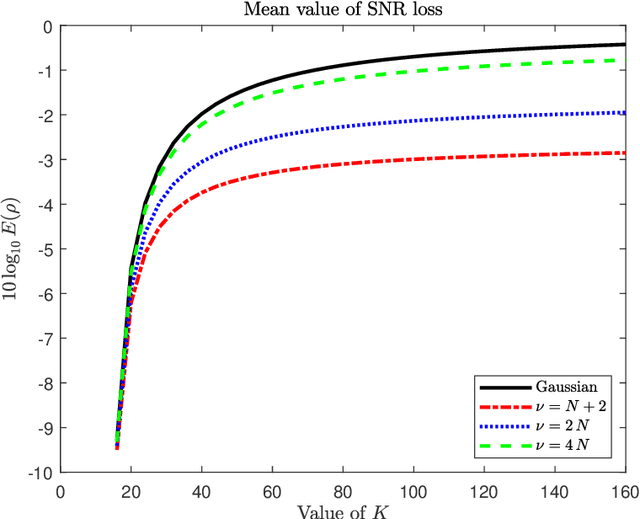
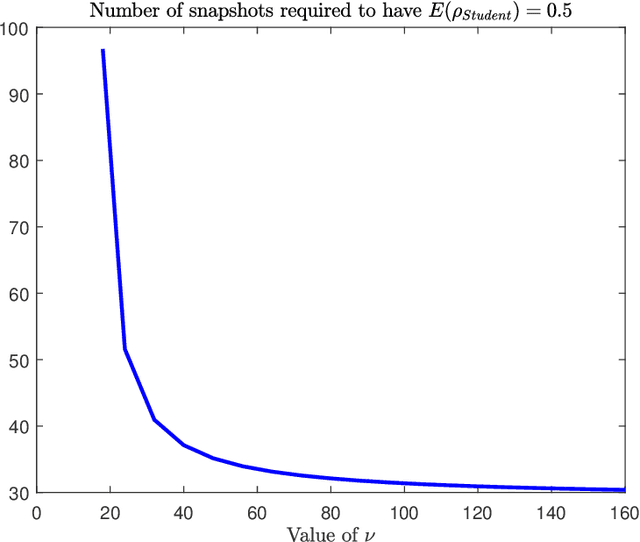
In this paper we analyze the behavior of adaptive filters or detectors when they are trained with $t$-distributed samples rather than Gaussian distributed samples. More precisely we investigate the impact on the distribution of some relevant statistics including the signal to noise ratio loss and the Gaussian generalized likelihood ratio test. Some properties of partitioned complex $F$ distributed matrices are derived which enable to obtain statistical representations in terms of independent chi-square distributed random variables. These representations are compared with their Gaussian counterparts and numerical simulations illustrate and quantify the induced degradation.

Joint Bayesian estimation of close subspaces from noisy measurements

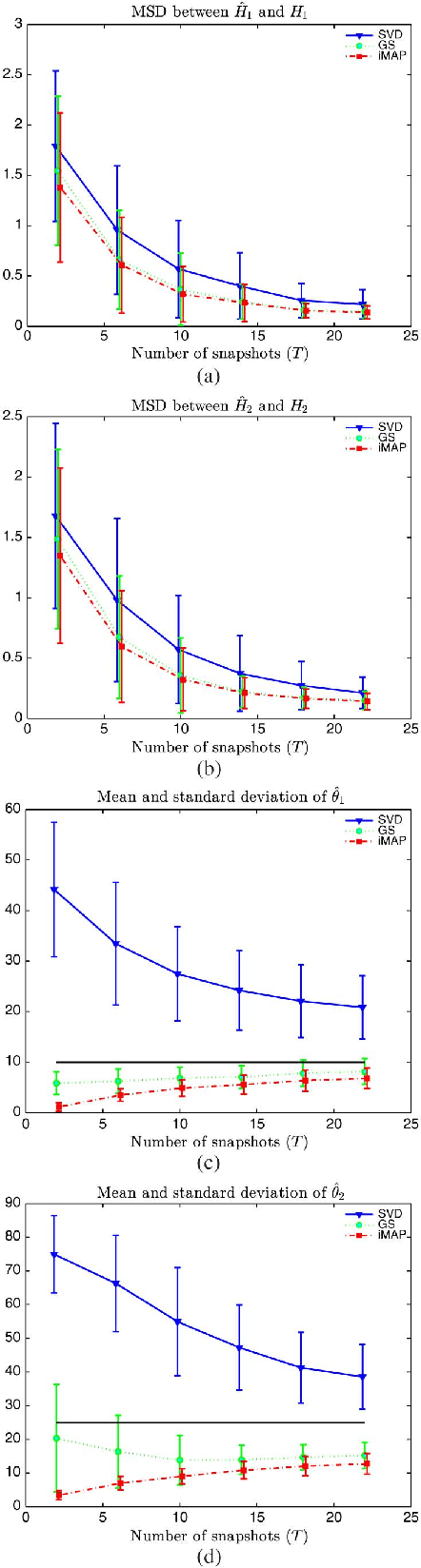
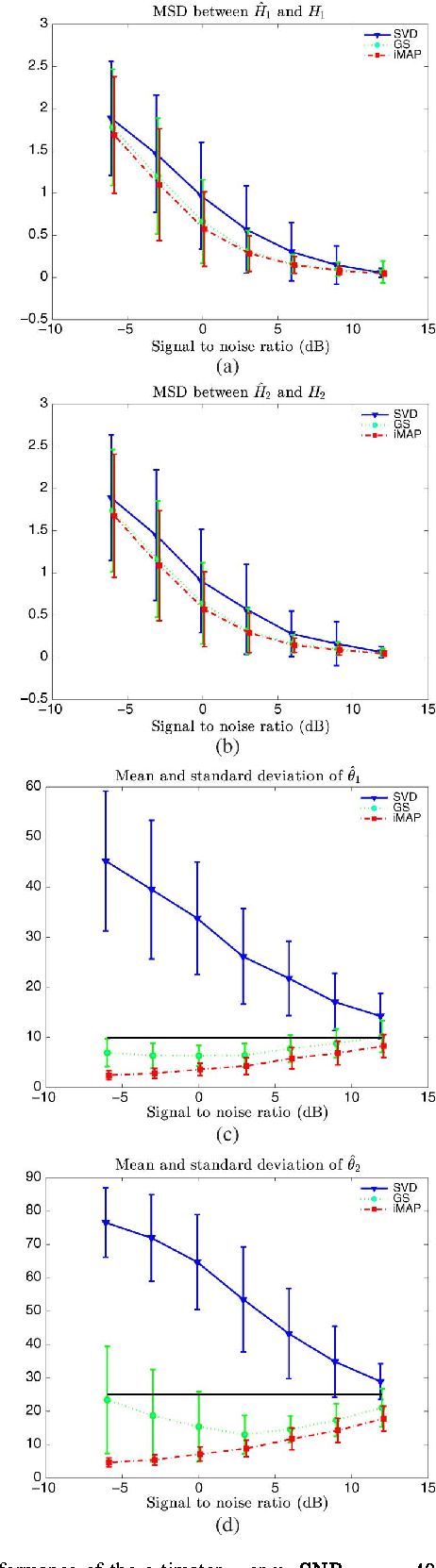
In this letter, we consider two sets of observations defined as subspace signals embedded in noise and we wish to analyze the distance between these two subspaces. The latter entails evaluating the angles between the subspaces, an issue reminiscent of the well-known Procrustes problem. A Bayesian approach is investigated where the subspaces of interest are considered as random with a joint prior distribution (namely a Bingham distribution), which allows the closeness of the two subspaces to be adjusted. Within this framework, the minimum mean-square distance estimator of both subspaces is formulated and implemented via a Gibbs sampler. A simpler scheme based on alternative maximum a posteriori estimation is also presented. The new schemes are shown to provide more accurate estimates of the angles between the subspaces, compared to singular value decomposition based independent estimation of the two subspaces.

Minimum mean square distance estimation of a subspace

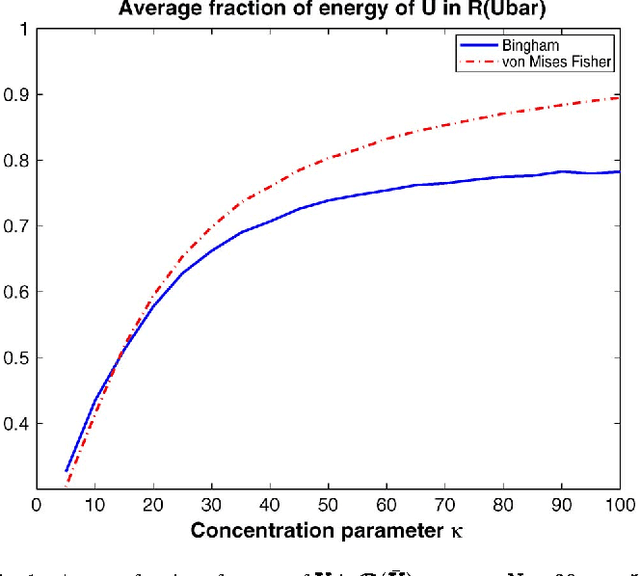
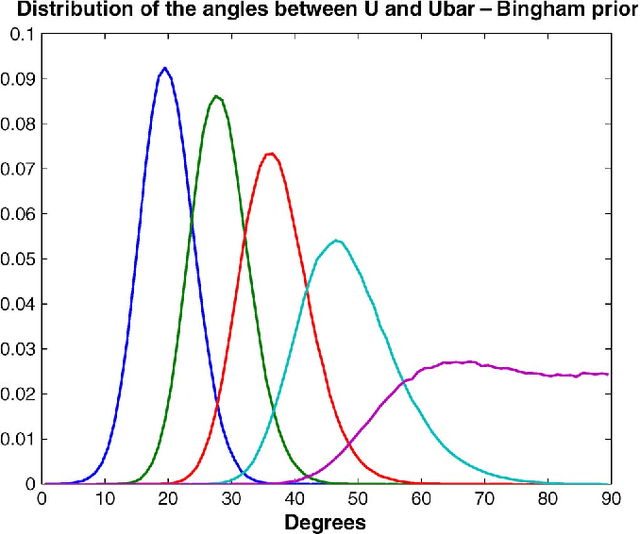
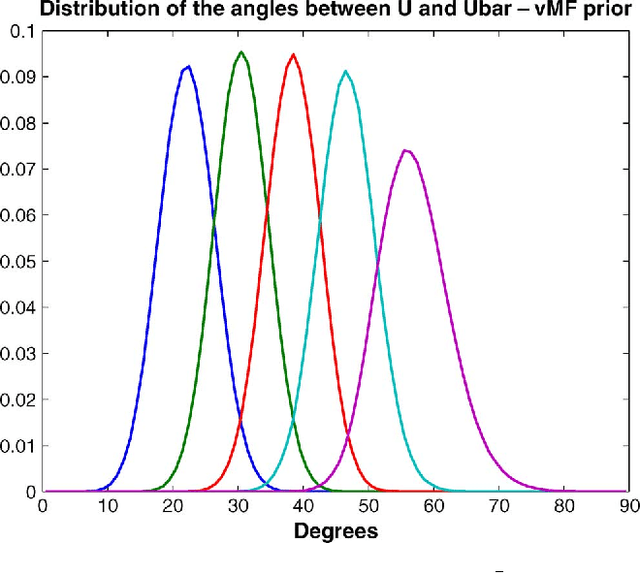
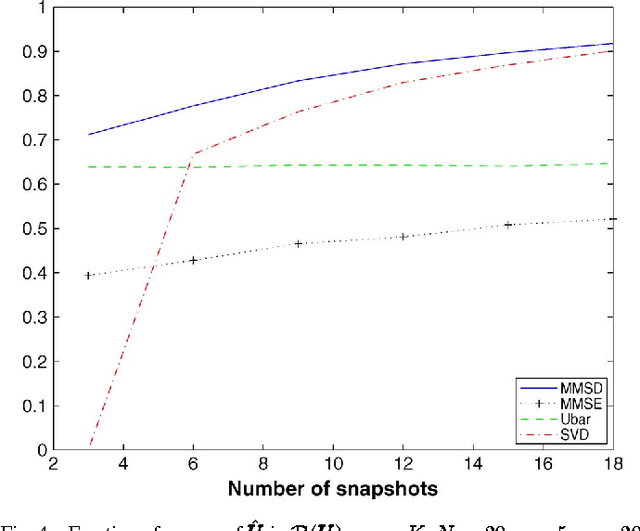
We consider the problem of subspace estimation in a Bayesian setting. Since we are operating in the Grassmann manifold, the usual approach which consists of minimizing the mean square error (MSE) between the true subspace $U$ and its estimate $\hat{U}$ may not be adequate as the MSE is not the natural metric in the Grassmann manifold. As an alternative, we propose to carry out subspace estimation by minimizing the mean square distance (MSD) between $U$ and its estimate, where the considered distance is a natural metric in the Grassmann manifold, viz. the distance between the projection matrices. We show that the resulting estimator is no longer the posterior mean of $U$ but entails computing the principal eigenvectors of the posterior mean of $U U^{T}$. Derivation of the MMSD estimator is carried out in a few illustrative examples including a linear Gaussian model for the data and a Bingham or von Mises Fisher prior distribution for $U$. In all scenarios, posterior distributions are derived and the MMSD estimator is obtained either analytically or implemented via a Markov chain Monte Carlo simulation method. The method is shown to provide accurate estimates even when the number of samples is lower than the dimension of $U$. An application to hyperspectral imagery is finally investigated.