MolecularIQ: Characterizing Chemical Reasoning Capabilities Through Symbolic Verification on Molecular Graphs

A molecule's properties are fundamentally determined by its composition and structure encoded in its molecular graph. Thus, reasoning about molecular properties requires the ability to parse and understand the molecular graph. Large Language Models (LLMs) are increasingly applied to chemistry, tackling tasks such as molecular name conversion, captioning, text-guided generation, and property or reaction prediction. Most existing benchmarks emphasize general chemical knowledge, rely on literature or surrogate labels that risk leakage or bias, or reduce evaluation to multiple-choice questions. We introduce MolecularIQ, a molecular structure reasoning benchmark focused exclusively on symbolically verifiable tasks. MolecularIQ enables fine-grained evaluation of reasoning over molecular graphs and reveals capability patterns that localize model failures to specific tasks and molecular structures. This provides actionable insights into the strengths and limitations of current chemistry LLMs and guides the development of models that reason faithfully over molecular structure.

Addressing Pitfalls in the Evaluation of Uncertainty Estimation Methods for Natural Language Generation

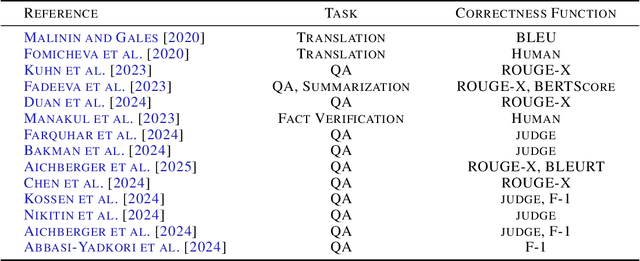
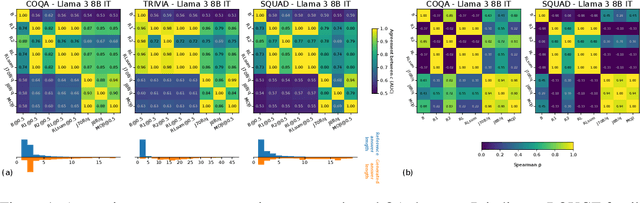
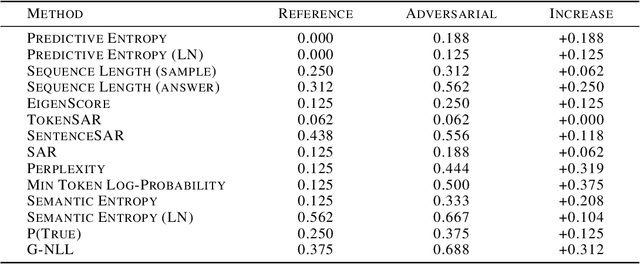
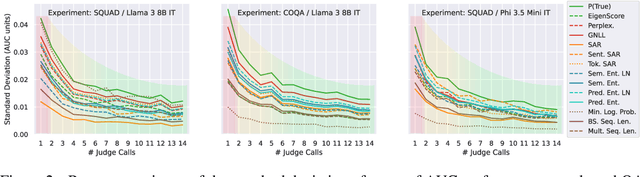
Hallucinations are a common issue that undermine the reliability of large language models (LLMs). Recent studies have identified a specific subset of hallucinations, known as confabulations, which arise due to predictive uncertainty of LLMs. To detect confabulations, various methods for estimating predictive uncertainty in natural language generation (NLG) have been developed. These methods are typically evaluated by correlating uncertainty estimates with the correctness of generated text, with question-answering (QA) datasets serving as the standard benchmark. However, commonly used approximate correctness functions have substantial disagreement between each other and, consequently, in the ranking of the uncertainty estimation methods. This allows one to inflate the apparent performance of uncertainty estimation methods. We propose using several alternative risk indicators for risk correlation experiments that improve robustness of empirical assessment of UE algorithms for NLG. For QA tasks, we show that marginalizing over multiple LLM-as-a-judge variants leads to reducing the evaluation biases. Furthermore, we explore structured tasks as well as out of distribution and perturbation detection tasks which provide robust and controllable risk indicators. Finally, we propose to use an Elo rating of uncertainty estimation methods to give an objective summarization over extensive evaluation settings.

Uncertainty Quantification for Regression using Proper Scoring Rules

Quantifying uncertainty of machine learning model predictions is essential for reliable decision-making, especially in safety-critical applications. Recently, uncertainty quantification (UQ) theory has advanced significantly, building on a firm basis of learning with proper scoring rules. However, these advances were focused on classification, while extending these ideas to regression remains challenging. In this work, we introduce a unified UQ framework for regression based on proper scoring rules, such as CRPS, logarithmic, squared error, and quadratic scores. We derive closed-form expressions for the resulting uncertainty measures under practical parametric assumptions and show how to estimate them using ensembles of models. In particular, the derived uncertainty measures naturally decompose into aleatoric and epistemic components. The framework recovers popular regression UQ measures based on predictive variance and differential entropy. Our broad evaluation on synthetic and real-world regression datasets provides guidance for selecting reliable UQ measures.

On Information-Theoretic Measures of Predictive Uncertainty

Reliable estimation of predictive uncertainty is crucial for machine learning applications, particularly in high-stakes scenarios where hedging against risks is essential. Despite its significance, a consensus on the correct measurement of predictive uncertainty remains elusive. In this work, we return to first principles to develop a fundamental framework of information-theoretic predictive uncertainty measures. Our proposed framework categorizes predictive uncertainty measures according to two factors: (I) The predicting model (II) The approximation of the true predictive distribution. Examining all possible combinations of these two factors, we derive a set of predictive uncertainty measures that includes both known and newly introduced ones. We empirically evaluate these measures in typical uncertainty estimation settings, such as misclassification detection, selective prediction, and out-of-distribution detection. The results show that no single measure is universal, but the effectiveness depends on the specific setting. Thus, our work provides clarity about the suitability of predictive uncertainty measures by clarifying their implicit assumptions and relationships.

Semantically Diverse Language Generation for Uncertainty Estimation in Language Models

Large language models (LLMs) can suffer from hallucinations when generating text. These hallucinations impede various applications in society and industry by making LLMs untrustworthy. Current LLMs generate text in an autoregressive fashion by predicting and appending text tokens. When an LLM is uncertain about the semantic meaning of the next tokens to generate, it is likely to start hallucinating. Thus, it has been suggested that hallucinations stem from predictive uncertainty. We introduce Semantically Diverse Language Generation (SDLG) to quantify predictive uncertainty in LLMs. SDLG steers the LLM to generate semantically diverse yet likely alternatives for an initially generated text. This approach provides a precise measure of aleatoric semantic uncertainty, detecting whether the initial text is likely to be hallucinated. Experiments on question-answering tasks demonstrate that SDLG consistently outperforms existing methods while being the most computationally efficient, setting a new standard for uncertainty estimation in LLMs.

Introducing an Improved Information-Theoretic Measure of Predictive Uncertainty

Applying a machine learning model for decision-making in the real world requires to distinguish what the model knows from what it does not. A critical factor in assessing the knowledge of a model is to quantify its predictive uncertainty. Predictive uncertainty is commonly measured by the entropy of the Bayesian model average (BMA) predictive distribution. Yet, the properness of this current measure of predictive uncertainty was recently questioned. We provide new insights regarding those limitations. Our analyses show that the current measure erroneously assumes that the BMA predictive distribution is equivalent to the predictive distribution of the true model that generated the dataset. Consequently, we introduce a theoretically grounded measure to overcome these limitations. We experimentally verify the benefits of our introduced measure of predictive uncertainty. We find that our introduced measure behaves more reasonably in controlled synthetic tasks. Moreover, our evaluations on ImageNet demonstrate that our introduced measure is advantageous in real-world applications utilizing predictive uncertainty.

Quantification of Uncertainty with Adversarial Models

Quantifying uncertainty is important for actionable predictions in real-world applications. A crucial part of predictive uncertainty quantification is the estimation of epistemic uncertainty, which is defined as an integral of the product between a divergence function and the posterior. Current methods such as Deep Ensembles or MC dropout underperform at estimating the epistemic uncertainty, since they primarily consider the posterior when sampling models. We suggest Quantification of Uncertainty with Adversarial Models (QUAM) to better estimate the epistemic uncertainty. QUAM identifies regions where the whole product under the integral is large, not just the posterior. Consequently, QUAM has lower approximation error of the epistemic uncertainty compared to previous methods. Models for which the product is large correspond to adversarial models (not adversarial examples!). Adversarial models have both a high posterior as well as a high divergence between their predictions and that of a reference model. Our experiments show that QUAM excels in capturing epistemic uncertainty for deep learning models and outperforms previous methods on challenging tasks in the vision domain.