Sampling from the Mean-Field Stationary Distribution

We study the complexity of sampling from the stationary distribution of a mean-field SDE, or equivalently, the complexity of minimizing a functional over the space of probability measures which includes an interaction term. Our main insight is to decouple the two key aspects of this problem: (1) approximation of the mean-field SDE via a finite-particle system, via uniform-in-time propagation of chaos, and (2) sampling from the finite-particle stationary distribution, via standard log-concave samplers. Our approach is conceptually simpler and its flexibility allows for incorporating the state-of-the-art for both algorithms and theory. This leads to improved guarantees in numerous settings, including better guarantees for optimizing certain two-layer neural networks in the mean-field regime.

Differential Equation Scaling Limits of Shaped and Unshaped Neural Networks

Recent analyses of neural networks with shaped activations (i.e. the activation function is scaled as the network size grows) have led to scaling limits described by differential equations. However, these results do not a priori tell us anything about "ordinary" unshaped networks, where the activation is unchanged as the network size grows. In this article, we find similar differential equation based asymptotic characterization for two types of unshaped networks. Firstly, we show that the following two architectures converge to the same infinite-depth-and-width limit at initialization: (i) a fully connected ResNet with a $d^{-1/2}$ factor on the residual branch, where $d$ is the network depth. (ii) a multilayer perceptron (MLP) with depth $d \ll$ width $n$ and shaped ReLU activation at rate $d^{-1/2}$. Secondly, for an unshaped MLP at initialization, we derive the first order asymptotic correction to the layerwise correlation. In particular, if $\rho_\ell$ is the correlation at layer $\ell$, then $q_t = \ell^2 (1 - \rho_\ell)$ with $t = \frac{\ell}{n}$ converges to an SDE with a singularity at $t=0$. These results together provide a connection between shaped and unshaped network architectures, and opens up the possibility of studying the effect of normalization methods and how it connects with shaping activation functions.

Depthwise Hyperparameter Transfer in Residual Networks: Dynamics and Scaling Limit

The cost of hyperparameter tuning in deep learning has been rising with model sizes, prompting practitioners to find new tuning methods using a proxy of smaller networks. One such proposal uses $\mu$P parameterized networks, where the optimal hyperparameters for small width networks transfer to networks with arbitrarily large width. However, in this scheme, hyperparameters do not transfer across depths. As a remedy, we study residual networks with a residual branch scale of $1/\sqrt{\text{depth}}$ in combination with the $\mu$P parameterization. We provide experiments demonstrating that residual architectures including convolutional ResNets and Vision Transformers trained with this parameterization exhibit transfer of optimal hyperparameters across width and depth on CIFAR-10 and ImageNet. Furthermore, our empirical findings are supported and motivated by theory. Using recent developments in the dynamical mean field theory (DMFT) description of neural network learning dynamics, we show that this parameterization of ResNets admits a well-defined feature learning joint infinite-width and infinite-depth limit and show convergence of finite-size network dynamics towards this limit.

The Shaped Transformer: Attention Models in the Infinite Depth-and-Width Limit

In deep learning theory, the covariance matrix of the representations serves as a proxy to examine the network's trainability. Motivated by the success of Transformers, we study the covariance matrix of a modified Softmax-based attention model with skip connections in the proportional limit of infinite-depth-and-width. We show that at initialization the limiting distribution can be described by a stochastic differential equation (SDE) indexed by the depth-to-width ratio. To achieve a well-defined stochastic limit, the Transformer's attention mechanism is modified by centering the Softmax output at identity, and scaling the Softmax logits by a width-dependent temperature parameter. We examine the stability of the network through the corresponding SDE, showing how the scale of both the drift and diffusion can be elegantly controlled with the aid of residual connections. The existence of a stable SDE implies that the covariance structure is well-behaved, even for very large depth and width, thus preventing the notorious issues of rank degeneracy in deep attention models. Finally, we show, through simulations, that the SDE provides a surprisingly good description of the corresponding finite-size model. We coin the name shaped Transformer for these architectural modifications.

Improved Discretization Analysis for Underdamped Langevin Monte Carlo

Underdamped Langevin Monte Carlo (ULMC) is an algorithm used to sample from unnormalized densities by leveraging the momentum of a particle moving in a potential well. We provide a novel analysis of ULMC, motivated by two central questions: (1) Can we obtain improved sampling guarantees beyond strong log-concavity? (2) Can we achieve acceleration for sampling? For (1), prior results for ULMC only hold under a log-Sobolev inequality together with a restrictive Hessian smoothness condition. Here, we relax these assumptions by removing the Hessian smoothness condition and by considering distributions satisfying a Poincar\'e inequality. Our analysis achieves the state of art dimension dependence, and is also flexible enough to handle weakly smooth potentials. As a byproduct, we also obtain the first KL divergence guarantees for ULMC without Hessian smoothness under strong log-concavity, which is based on a new result on the log-Sobolev constant along the underdamped Langevin diffusion. For (2), the recent breakthrough of Cao, Lu, and Wang (2020) established the first accelerated result for sampling in continuous time via PDE methods. Our discretization analysis translates their result into an algorithmic guarantee, which indeed enjoys better condition number dependence than prior works on ULMC, although we leave open the question of full acceleration in discrete time. Both (1) and (2) necessitate R\'enyi discretization bounds, which are more challenging than the typically used Wasserstein coupling arguments. We address this using a flexible discretization analysis based on Girsanov's theorem that easily extends to more general settings.

The Neural Covariance SDE: Shaped Infinite Depth-and-Width Networks at Initialization

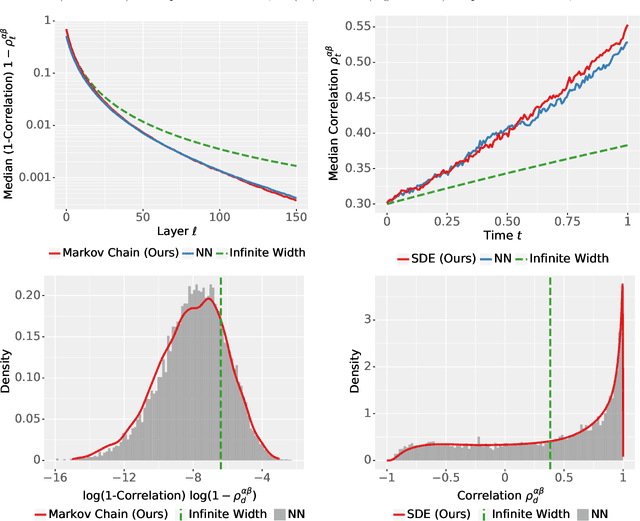
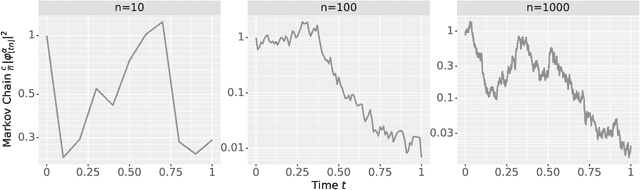
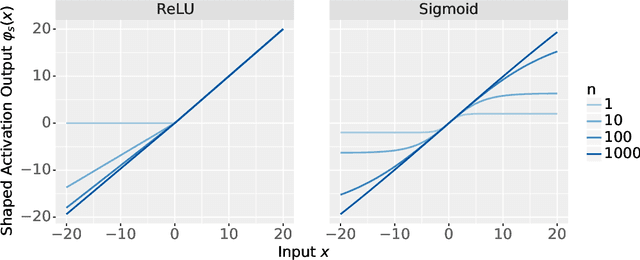
The logit outputs of a feedforward neural network at initialization are conditionally Gaussian, given a random covariance matrix defined by the penultimate layer. In this work, we study the distribution of this random matrix. Recent work has shown that shaping the activation function as network depth grows large is necessary for this covariance matrix to be non-degenerate. However, the current infinite-width-style understanding of this shaping method is unsatisfactory for large depth: infinite-width analyses ignore the microscopic fluctuations from layer to layer, but these fluctuations accumulate over many layers. To overcome this shortcoming, we study the random covariance matrix in the shaped infinite-depth-and-width limit. We identify the precise scaling of the activation function necessary to arrive at a non-trivial limit, and show that the random covariance matrix is governed by a stochastic differential equation (SDE) that we call the Neural Covariance SDE. Using simulations, we show that the SDE closely matches the distribution of the random covariance matrix of finite networks. Additionally, we recover an if-and-only-if condition for exploding and vanishing norms of large shaped networks based on the activation function.

Analysis of Langevin Monte Carlo from Poincaré to Log-Sobolev

Classically, the continuous-time Langevin diffusion converges exponentially fast to its stationary distribution $\pi$ under the sole assumption that $\pi$ satisfies a Poincar\'e inequality. Using this fact to provide guarantees for the discrete-time Langevin Monte Carlo (LMC) algorithm, however, is considerably more challenging due to the need for working with chi-squared or R\'enyi divergences, and prior works have largely focused on strongly log-concave targets. In this work, we provide the first convergence guarantees for LMC assuming that $\pi$ satisfies either a Lata{\l}a--Oleszkiewicz or modified log-Sobolev inequality, which interpolates between the Poincar\'e and log-Sobolev settings. Unlike prior works, our results allow for weak smoothness and do not require convexity or dissipativity conditions.

The Future is Log-Gaussian: ResNets and Their Infinite-Depth-and-Width Limit at Initialization

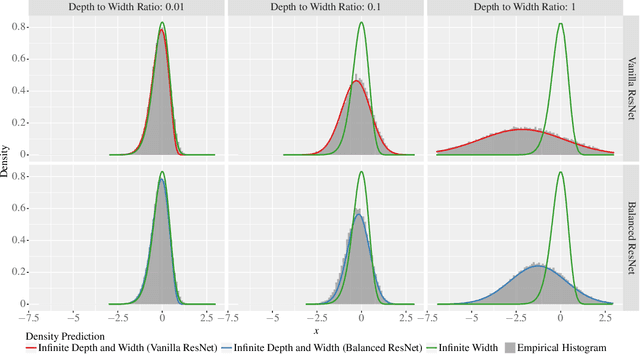
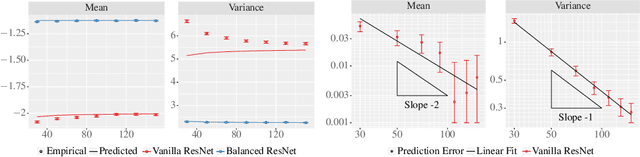
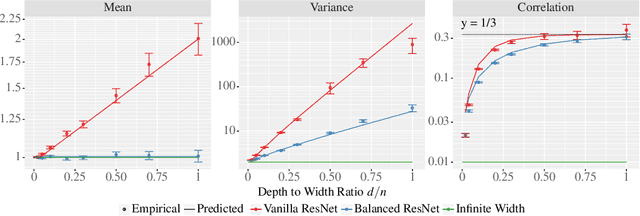
Theoretical results show that neural networks can be approximated by Gaussian processes in the infinite-width limit. However, for fully connected networks, it has been previously shown that for any fixed network width, $n$, the Gaussian approximation gets worse as the network depth, $d$, increases. Given that modern networks are deep, this raises the question of how well modern architectures, like ResNets, are captured by the infinite-width limit. To provide a better approximation, we study ReLU ResNets in the infinite-depth-and-width limit, where both depth and width tend to infinity as their ratio, $d/n$, remains constant. In contrast to the Gaussian infinite-width limit, we show theoretically that the network exhibits log-Gaussian behaviour at initialization in the infinite-depth-and-width limit, with parameters depending on the ratio $d/n$. Using Monte Carlo simulations, we demonstrate that even basic properties of standard ResNet architectures are poorly captured by the Gaussian limit, but remarkably well captured by our log-Gaussian limit. Moreover, our analysis reveals that ReLU ResNets at initialization are hypoactivated: fewer than half of the ReLUs are activated. Additionally, we calculate the interlayer correlations, which have the effect of exponentially increasing the variance of the network output. Based on our analysis, we introduce Balanced ResNets, a simple architecture modification, which eliminates hypoactivation and interlayer correlations and is more amenable to theoretical analysis.

Higher Order Generalization Error for First Order Discretization of Langevin Diffusion

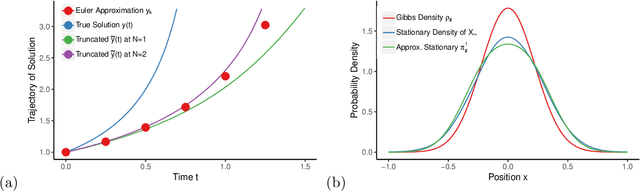
We propose a novel approach to analyze generalization error for discretizations of Langevin diffusion, such as the stochastic gradient Langevin dynamics (SGLD). For an $\epsilon$ tolerance of expected generalization error, it is known that a first order discretization can reach this target if we run $\Omega(\epsilon^{-1} \log (\epsilon^{-1}) )$ iterations with $\Omega(\epsilon^{-1})$ samples. In this article, we show that with additional smoothness assumptions, even first order methods can achieve arbitrarily runtime complexity. More precisely, for each $N>0$, we provide a sufficient smoothness condition on the loss function such that a first order discretization can reach $\epsilon$ expected generalization error given $\Omega( \epsilon^{-1/N} \log (\epsilon^{-1}) )$ iterations with $\Omega(\epsilon^{-1})$ samples.

Riemannian Langevin Algorithm for Solving Semidefinite Programs

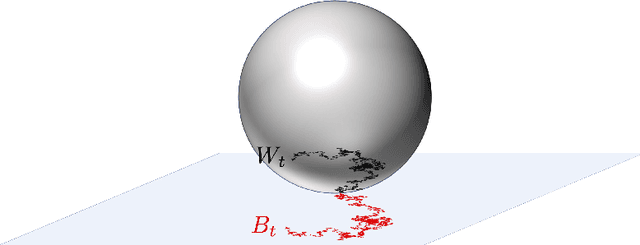
We propose a Langevin diffusion-based algorithm for non-convex optimization and sampling on a product manifold of spheres. Under a logarithmic Sobolev inequality, we establish a guarantee for finite iteration convergence to the Gibbs distribution in terms of Kullback-Leibler divergence. We show that with an appropriate temperature choice, the suboptimality gap to the global minimum is guaranteed to be arbitrarily small with high probability. As an application, we analyze the proposed Langevin algorithm for solving the Burer-Monteiro relaxation of a semidefinite program (SDP). In particular, we establish a logarithmic Sobolev inequality for the Burer-Monteiro problem when there are no spurious local minima; hence implying a fast escape from saddle points. Combining the results, we then provide a global optimality guarantee for the SDP and the Max-Cut problem. More precisely, we show the Langevin algorithm achieves $\epsilon$-multiplicative accuracy with high probability in $\widetilde{\Omega}( n^2 \epsilon^{-3} )$ iterations, where $n$ is the size of the cost matrix.