Graph Random Features for Scalable Gaussian Processes

We study the application of graph random features (GRFs) - a recently introduced stochastic estimator of graph node kernels - to scalable Gaussian processes on discrete input spaces. We prove that (under mild assumptions) Bayesian inference with GRFs enjoys $O(N^{3/2})$ time complexity with respect to the number of nodes $N$, compared to $O(N^3)$ for exact kernels. Substantial wall-clock speedups and memory savings unlock Bayesian optimisation on graphs with over $10^6$ nodes on a single computer chip, whilst preserving competitive performance.

Improved Discretization Analysis for Underdamped Langevin Monte Carlo

Underdamped Langevin Monte Carlo (ULMC) is an algorithm used to sample from unnormalized densities by leveraging the momentum of a particle moving in a potential well. We provide a novel analysis of ULMC, motivated by two central questions: (1) Can we obtain improved sampling guarantees beyond strong log-concavity? (2) Can we achieve acceleration for sampling? For (1), prior results for ULMC only hold under a log-Sobolev inequality together with a restrictive Hessian smoothness condition. Here, we relax these assumptions by removing the Hessian smoothness condition and by considering distributions satisfying a Poincar\'e inequality. Our analysis achieves the state of art dimension dependence, and is also flexible enough to handle weakly smooth potentials. As a byproduct, we also obtain the first KL divergence guarantees for ULMC without Hessian smoothness under strong log-concavity, which is based on a new result on the log-Sobolev constant along the underdamped Langevin diffusion. For (2), the recent breakthrough of Cao, Lu, and Wang (2020) established the first accelerated result for sampling in continuous time via PDE methods. Our discretization analysis translates their result into an algorithmic guarantee, which indeed enjoys better condition number dependence than prior works on ULMC, although we leave open the question of full acceleration in discrete time. Both (1) and (2) necessitate R\'enyi discretization bounds, which are more challenging than the typically used Wasserstein coupling arguments. We address this using a flexible discretization analysis based on Girsanov's theorem that easily extends to more general settings.

Towards a Theory of Non-Log-Concave Sampling: First-Order Stationarity Guarantees for Langevin Monte Carlo

For the task of sampling from a density $\pi \propto \exp(-V)$ on $\mathbb{R}^d$, where $V$ is possibly non-convex but $L$-gradient Lipschitz, we prove that averaged Langevin Monte Carlo outputs a sample with $\varepsilon$-relative Fisher information after $O( L^2 d^2/\varepsilon^2)$ iterations. This is the sampling analogue of complexity bounds for finding an $\varepsilon$-approximate first-order stationary points in non-convex optimization and therefore constitutes a first step towards the general theory of non-log-concave sampling. We discuss numerous extensions and applications of our result; in particular, it yields a new state-of-the-art guarantee for sampling from distributions which satisfy a Poincar\'e inequality.

Analysis of Langevin Monte Carlo from Poincaré to Log-Sobolev

Classically, the continuous-time Langevin diffusion converges exponentially fast to its stationary distribution $\pi$ under the sole assumption that $\pi$ satisfies a Poincar\'e inequality. Using this fact to provide guarantees for the discrete-time Langevin Monte Carlo (LMC) algorithm, however, is considerably more challenging due to the need for working with chi-squared or R\'enyi divergences, and prior works have largely focused on strongly log-concave targets. In this work, we provide the first convergence guarantees for LMC assuming that $\pi$ satisfies either a Lata{\l}a--Oleszkiewicz or modified log-Sobolev inequality, which interpolates between the Poincar\'e and log-Sobolev settings. Unlike prior works, our results allow for weak smoothness and do not require convexity or dissipativity conditions.

Neural Natural Language Processing for Unstructured Data in Electronic Health Records: a Review

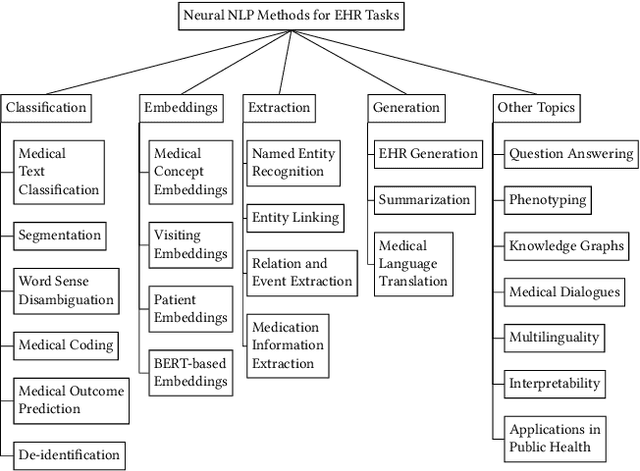
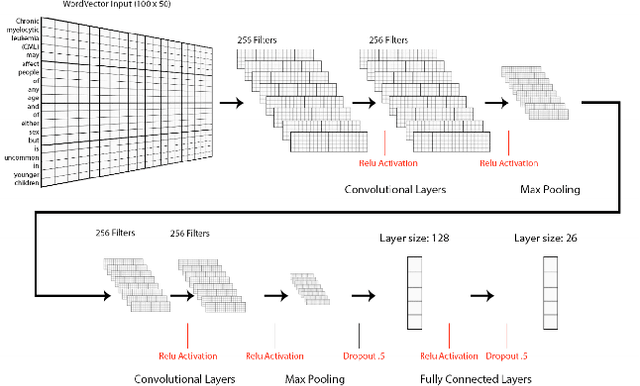
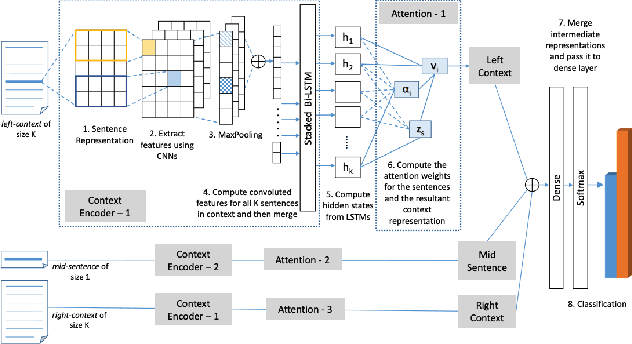
Electronic health records (EHRs), digital collections of patient healthcare events and observations, are ubiquitous in medicine and critical to healthcare delivery, operations, and research. Despite this central role, EHRs are notoriously difficult to process automatically. Well over half of the information stored within EHRs is in the form of unstructured text (e.g. provider notes, operation reports) and remains largely untapped for secondary use. Recently, however, newer neural network and deep learning approaches to Natural Language Processing (NLP) have made considerable advances, outperforming traditional statistical and rule-based systems on a variety of tasks. In this survey paper, we summarize current neural NLP methods for EHR applications. We focus on a broad scope of tasks, namely, classification and prediction, word embeddings, extraction, generation, and other topics such as question answering, phenotyping, knowledge graphs, medical dialogue, multilinguality, interpretability, etc.