DocVLM: Make Your VLM an Efficient Reader

Vision-Language Models (VLMs) excel in diverse visual tasks but face challenges in document understanding, which requires fine-grained text processing. While typical visual tasks perform well with low-resolution inputs, reading-intensive applications demand high-resolution, resulting in significant computational overhead. Using OCR-extracted text in VLM prompts partially addresses this issue but underperforms compared to full-resolution counterpart, as it lacks the complete visual context needed for optimal performance. We introduce DocVLM, a method that integrates an OCR-based modality into VLMs to enhance document processing while preserving original weights. Our approach employs an OCR encoder to capture textual content and layout, compressing these into a compact set of learned queries incorporated into the VLM. Comprehensive evaluations across leading VLMs show that DocVLM significantly reduces reliance on high-resolution images for document understanding. In limited-token regimes (448$\times$448), DocVLM with 64 learned queries improves DocVQA results from 56.0% to 86.6% when integrated with InternVL2 and from 84.4% to 91.2% with Qwen2-VL. In LLaVA-OneVision, DocVLM achieves improved results while using 80% less image tokens. The reduced token usage allows processing multiple pages effectively, showing impressive zero-shot results on DUDE and state-of-the-art performance on MP-DocVQA, highlighting DocVLM's potential for applications requiring high-performance and efficiency.

How Uniform Random Weights Induce Non-uniform Bias: Typical Interpolating Neural Networks Generalize with Narrow Teachers

Background. A main theoretical puzzle is why over-parameterized Neural Networks (NNs) generalize well when trained to zero loss (i.e., so they interpolate the data). Usually, the NN is trained with Stochastic Gradient Descent (SGD) or one of its variants. However, recent empirical work examined the generalization of a random NN that interpolates the data: the NN was sampled from a seemingly uniform prior over the parameters, conditioned on that the NN perfectly classifying the training set. Interestingly, such a NN sample typically generalized as well as SGD-trained NNs. Contributions. We prove that such a random NN interpolator typically generalizes well if there exists an underlying narrow ``teacher NN" that agrees with the labels. Specifically, we show that such a `flat' prior over the NN parametrization induces a rich prior over the NN functions, due to the redundancy in the NN structure. In particular, this creates a bias towards simpler functions, which require less relevant parameters to represent -- enabling learning with a sample complexity approximately proportional to the complexity of the teacher (roughly, the number of non-redundant parameters), rather than the student's.

The Implicit Bias of Minima Stability in Multivariate Shallow ReLU Networks

We study the type of solutions to which stochastic gradient descent converges when used to train a single hidden-layer multivariate ReLU network with the quadratic loss. Our results are based on a dynamical stability analysis. In the univariate case, it was shown that linearly stable minima correspond to network functions (predictors), whose second derivative has a bounded weighted $L^1$ norm. Notably, the bound gets smaller as the step size increases, implying that training with a large step size leads to `smoother' predictors. Here we generalize this result to the multivariate case, showing that a similar result applies to the Laplacian of the predictor. We demonstrate the tightness of our bound on the MNIST dataset, and show that it accurately captures the behavior of the solutions as a function of the step size. Additionally, we prove a depth separation result on the approximation power of ReLU networks corresponding to stable minima of the loss. Specifically, although shallow ReLU networks are universal approximators, we prove that stable shallow networks are not. Namely, there is a function that cannot be well-approximated by stable single hidden-layer ReLU networks trained with a non-vanishing step size. This is while the same function can be realized as a stable two hidden-layer ReLU network. Finally, we prove that if a function is sufficiently smooth (in a Sobolev sense) then it can be approximated arbitrarily well using shallow ReLU networks that correspond to stable solutions of gradient descent.

Gradient Descent Monotonically Decreases the Sharpness of Gradient Flow Solutions in Scalar Networks and Beyond

Recent research shows that when Gradient Descent (GD) is applied to neural networks, the loss almost never decreases monotonically. Instead, the loss oscillates as gradient descent converges to its ''Edge of Stability'' (EoS). Here, we find a quantity that does decrease monotonically throughout GD training: the sharpness attained by the gradient flow solution (GFS)-the solution that would be obtained if, from now until convergence, we train with an infinitesimal step size. Theoretically, we analyze scalar neural networks with the squared loss, perhaps the simplest setting where the EoS phenomena still occur. In this model, we prove that the GFS sharpness decreases monotonically. Using this result, we characterize settings where GD provably converges to the EoS in scalar networks. Empirically, we show that GD monotonically decreases the GFS sharpness in a squared regression model as well as practical neural network architectures.

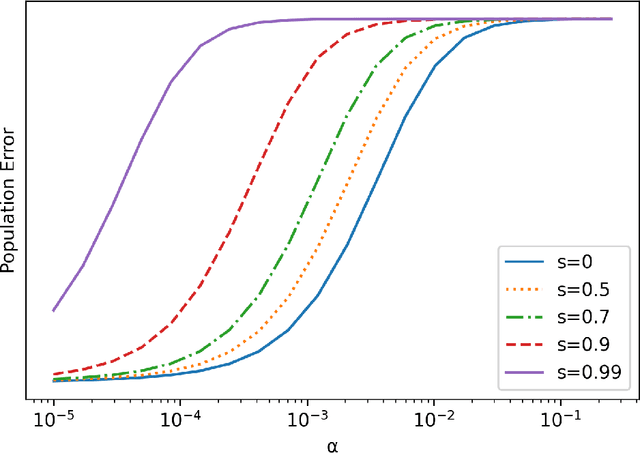
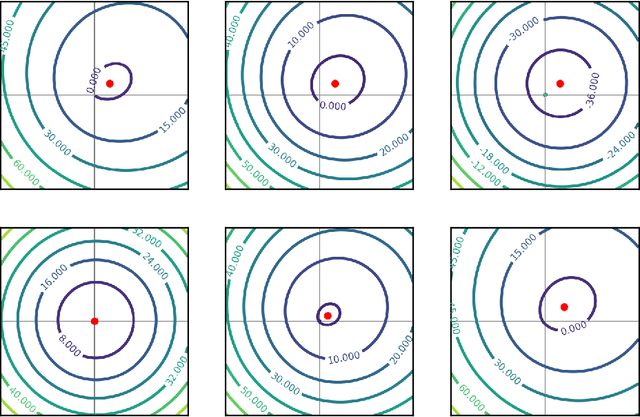
On the Implicit Bias of Initialization Shape: Beyond Infinitesimal Mirror Descent

Recent work has highlighted the role of initialization scale in determining the structure of the solutions that gradient methods converge to. In particular, it was shown that large initialization leads to the neural tangent kernel regime solution, whereas small initialization leads to so called "rich regimes". However, the initialization structure is richer than the overall scale alone and involves relative magnitudes of different weights and layers in the network. Here we show that these relative scales, which we refer to as initialization shape, play an important role in determining the learned model. We develop a novel technique for deriving the inductive bias of gradient-flow and use it to obtain closed-form implicit regularizers for multiple cases of interest.

At Stability's Edge: How to Adjust Hyperparameters to Preserve Minima Selection in Asynchronous Training of Neural Networks?

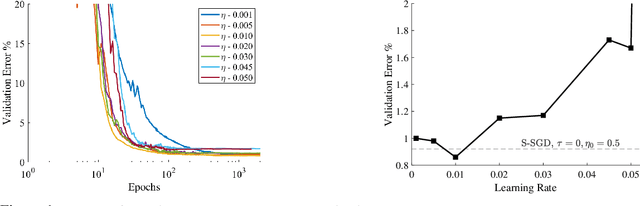
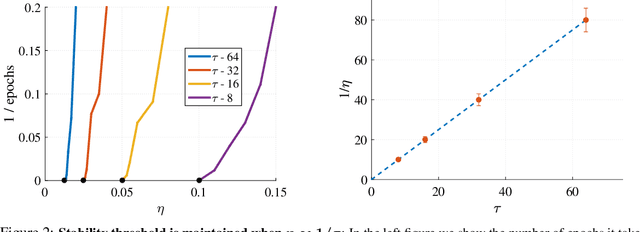
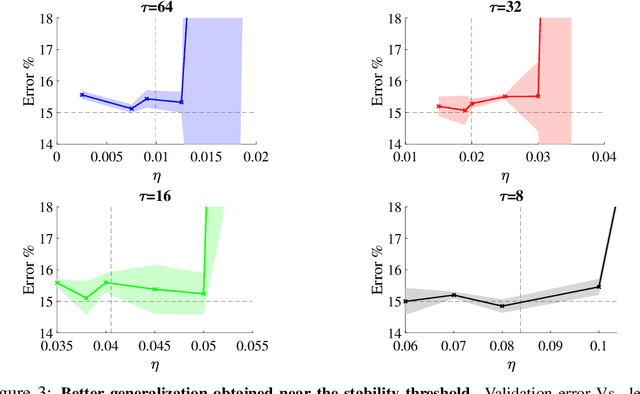
Background: Recent developments have made it possible to accelerate neural networks training significantly using large batch sizes and data parallelism. Training in an asynchronous fashion, where delay occurs, can make training even more scalable. However, asynchronous training has its pitfalls, mainly a degradation in generalization, even after convergence of the algorithm. This gap remains not well understood, as theoretical analysis so far mainly focused on the convergence rate of asynchronous methods. Contributions: We examine asynchronous training from the perspective of dynamical stability. We find that the degree of delay interacts with the learning rate, to change the set of minima accessible by an asynchronous stochastic gradient descent algorithm. We derive closed-form rules on how the learning rate could be changed, while keeping the accessible set the same. Specifically, for high delay values, we find that the learning rate should be kept inversely proportional to the delay. We then extend this analysis to include momentum. We find momentum should be either turned off, or modified to improve training stability. We provide empirical experiments to validate our theoretical findings.

Lexicographic and Depth-Sensitive Margins in Homogeneous and Non-Homogeneous Deep Models

With an eye toward understanding complexity control in deep learning, we study how infinitesimal regularization or gradient descent optimization lead to margin maximizing solutions in both homogeneous and non-homogeneous models, extending previous work that focused on infinitesimal regularization only in homogeneous models. To this end we study the limit of loss minimization with a diverging norm constraint (the "constrained path"), relate it to the limit of a "margin path" and characterize the resulting solution. For non-homogeneous ensemble models, which output is a sum of homogeneous sub-models, we show that this solution discards the shallowest sub-models if they are unnecessary. For homogeneous models, we show convergence to a "lexicographic max-margin solution", and provide conditions under which max-margin solutions are also attained as the limit of unconstrained gradient descent.

Convergence of Gradient Descent on Separable Data

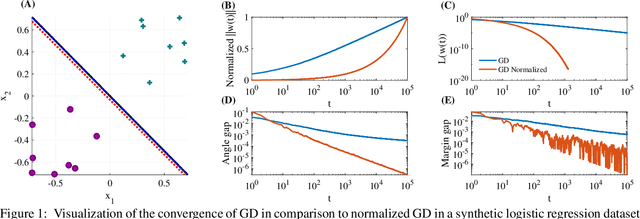
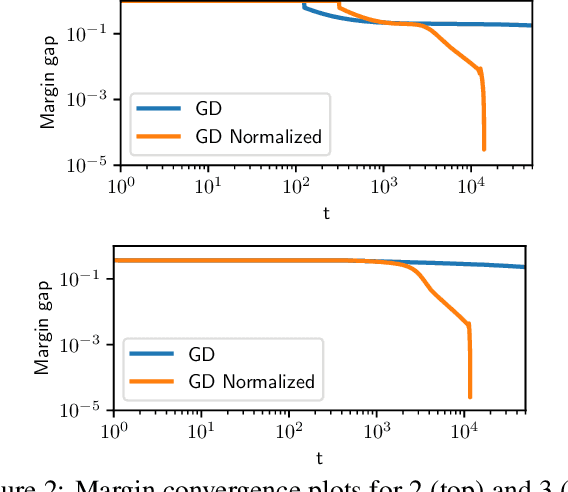
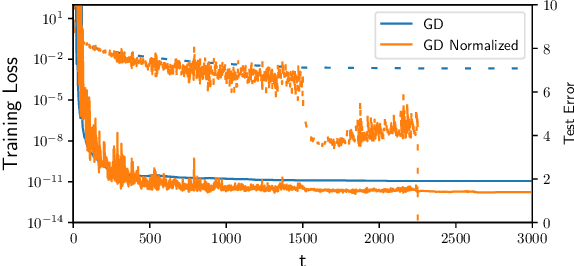
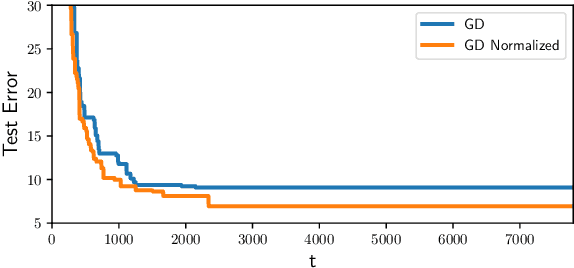
The implicit bias of gradient descent is not fully understood even in simple linear classification tasks (e.g., logistic regression). Soudry et al. (2018) studied this bias on separable data, where there are multiple solutions that correctly classify the data. It was found that, when optimizing monotonically decreasing loss functions with exponential tails using gradient descent, the linear classifier specified by the gradient descent iterates converge to the $L_2$ max margin separator. However, the convergence rate to the maximum margin solution with fixed step size was found to be extremely slow: $1/\log(t)$. Here we examine how the convergence is influenced by using different loss functions and by using variable step sizes. First, we calculate the convergence rate for loss functions with poly-exponential tails near $\exp(-u^{\nu})$. We prove that $\nu=1$ yields the optimal convergence rate in the range $\nu>0.25$. Based on further analysis we conjecture that this remains the optimal rate for $\nu \leq 0.25$, and even for sub-poly-exponential tails --- until loss functions with polynomial tails no longer converge to the max margin. Second, we prove the convergence rate could be improved to $(\log t) /\sqrt{t}$ for the exponential loss, by using aggressive step sizes which compensate for the rapidly vanishing gradients.

Stochastic Gradient Descent on Separable Data: Exact Convergence with a Fixed Learning Rate

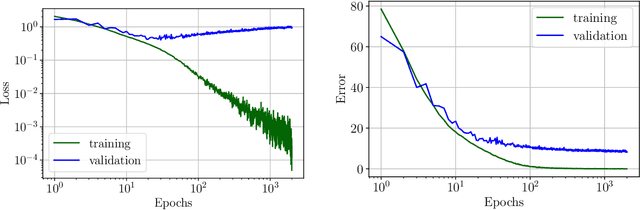
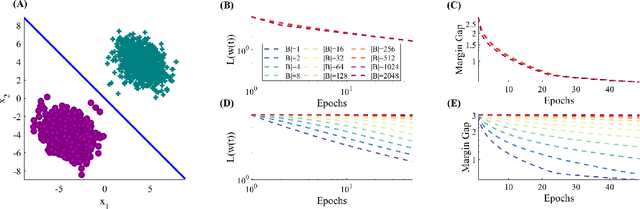
Stochastic Gradient Descent (SGD) is a central tool in machine learning. We prove that SGD converges to zero loss, even with a fixed learning rate --- in the special case of linear classifiers with smooth monotone loss functions, optimized on linearly separable data. Previous proofs with an exact asymptotic convergence of SGD required a learning rate that asymptotically vanishes to zero, or averaging of the SGD iterates. Furthermore, if the loss function has an exponential tail (e.g., logistic regression), then we prove that with SGD the weight vector converges in direction to the $L_2$ max margin vector as $O(1/\log(t))$ for almost all separable datasets, and the loss converges as $O(1/t)$ --- similarly to gradient descent. These results suggest an explanation to the similar behavior observed in deep networks when trained with SGD.

The Implicit Bias of Gradient Descent on Separable Data

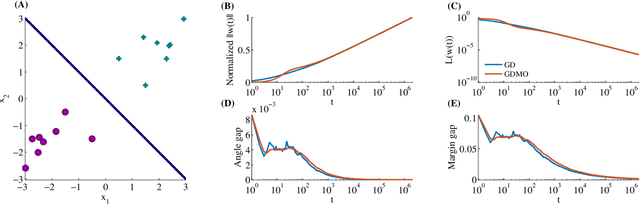
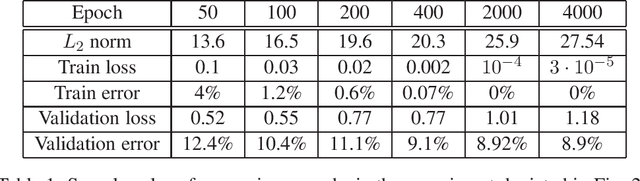
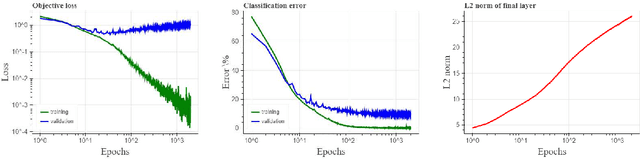
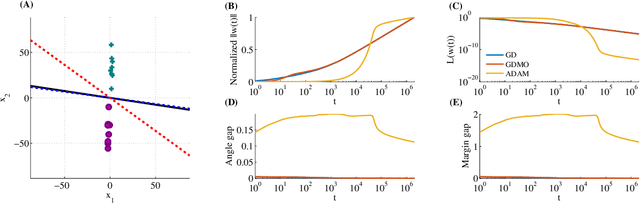
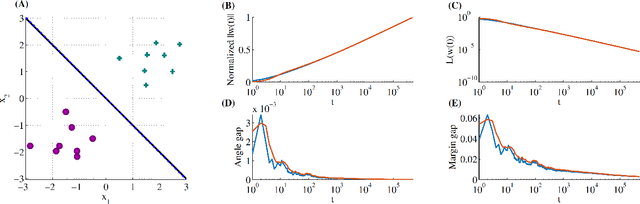
We show that gradient descent on an unregularized logistic regression problem, for linearly separable datasets, converges to the direction of the max-margin (hard margin SVM) solution. The result generalizes also to other monotone decreasing loss functions with an infimum at infinity, to multi-class problems, and to training a weight layer in a deep network in a certain restricted setting. Furthermore, we show this convergence is very slow, and only logarithmic in the convergence of the loss itself. This can help explain the benefit of continuing to optimize the logistic or cross-entropy loss even after the training error is zero and the training loss is extremely small, and, as we show, even if the validation loss increases. Our methodology can also aid in understanding implicit regularization in more complex models and with other optimization methods.