How Uniform Random Weights Induce Non-uniform Bias: Typical Interpolating Neural Networks Generalize with Narrow Teachers

Background. A main theoretical puzzle is why over-parameterized Neural Networks (NNs) generalize well when trained to zero loss (i.e., so they interpolate the data). Usually, the NN is trained with Stochastic Gradient Descent (SGD) or one of its variants. However, recent empirical work examined the generalization of a random NN that interpolates the data: the NN was sampled from a seemingly uniform prior over the parameters, conditioned on that the NN perfectly classifying the training set. Interestingly, such a NN sample typically generalized as well as SGD-trained NNs. Contributions. We prove that such a random NN interpolator typically generalizes well if there exists an underlying narrow ``teacher NN" that agrees with the labels. Specifically, we show that such a `flat' prior over the NN parametrization induces a rich prior over the NN functions, due to the redundancy in the NN structure. In particular, this creates a bias towards simpler functions, which require less relevant parameters to represent -- enabling learning with a sample complexity approximately proportional to the complexity of the teacher (roughly, the number of non-redundant parameters), rather than the student's.

A Theoretical Analysis of Fine-tuning with Linear Teachers

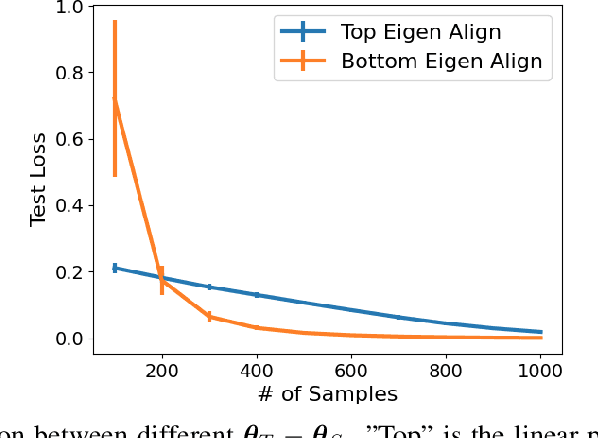
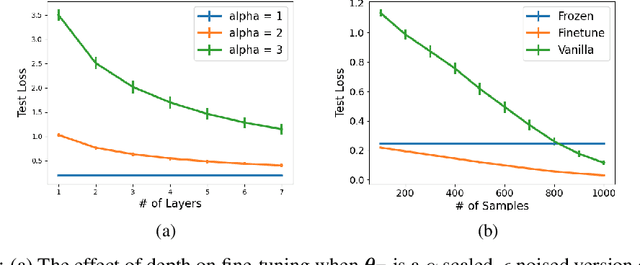
Fine-tuning is a common practice in deep learning, achieving excellent generalization results on downstream tasks using relatively little training data. Although widely used in practice, it is lacking strong theoretical understanding. We analyze the sample complexity of this scheme for regression with linear teachers in several architectures. Intuitively, the success of fine-tuning depends on the similarity between the source tasks and the target task, however measuring it is non trivial. We show that a relevant measure considers the relation between the source task, the target task and the covariance structure of the target data. In the setting of linear regression, we show that under realistic settings a substantial sample complexity reduction is plausible when the above measure is low. For deep linear regression, we present a novel result regarding the inductive bias of gradient-based training when the network is initialized with pretrained weights. Using this result we show that the similarity measure for this setting is also affected by the depth of the network. We further present results on shallow ReLU models, and analyze the dependence of sample complexity there on source and target tasks. We empirically demonstrate our results for both synthetic and realistic data.

Towards Understanding Learning in Neural Networks with Linear Teachers

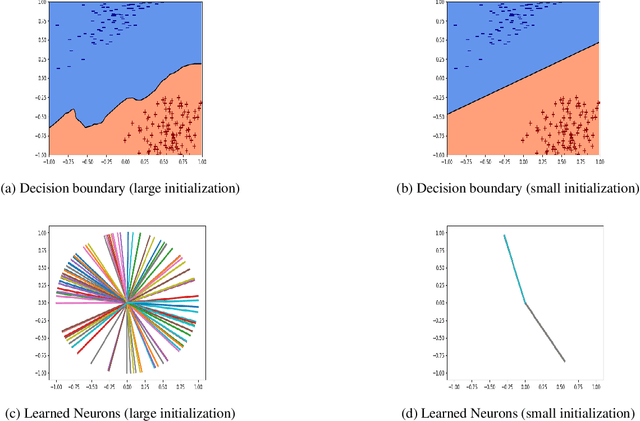
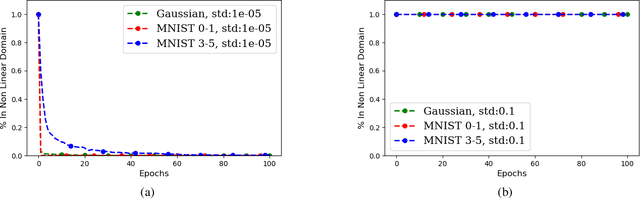
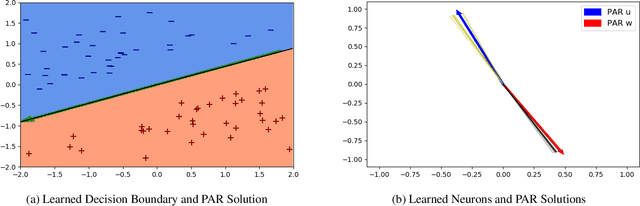
Can a neural network minimizing cross-entropy learn linearly separable data? Despite progress in the theory of deep learning, this question remains unsolved. Here we prove that SGD globally optimizes this learning problem for a two-layer network with Leaky ReLU activations. The learned network can in principle be very complex. However, empirical evidence suggests that it often turns out to be approximately linear. We provide theoretical support for this phenomenon by proving that if network weights converge to two weight clusters, this will imply an approximately linear decision boundary. Finally, we show a condition on the optimization that leads to weight clustering. We provide empirical results that validate our theoretical analysis.

On the Inductive Bias of a CNN for Orthogonal Patterns Distributions

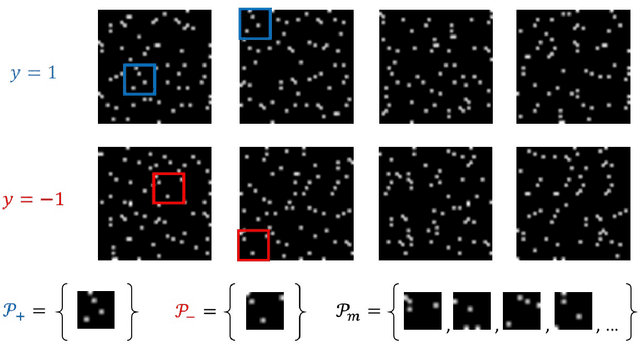
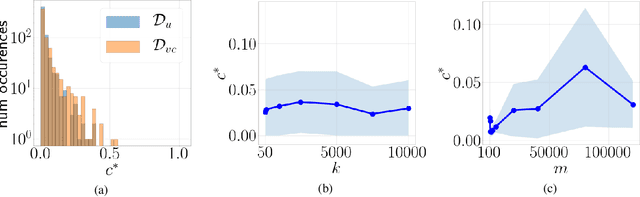
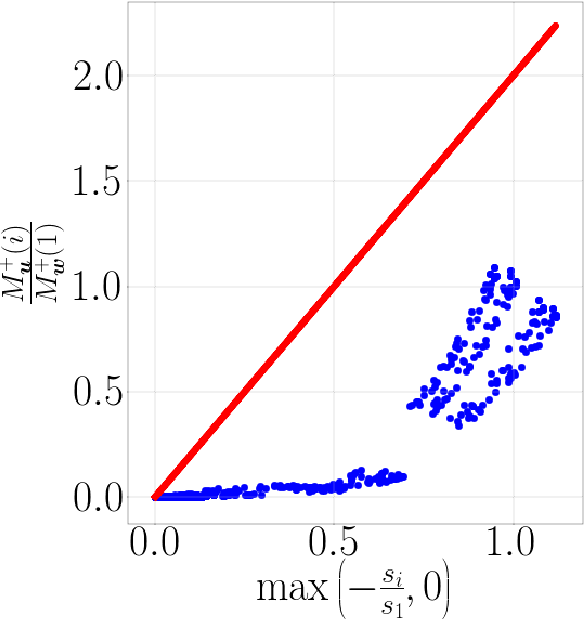
Training overparameterized convolutional neural networks with gradient based methods is the most successful learning method for image classification. However, its theoretical properties are far from understood even for very simple learning tasks. In this work, we consider a simplified image classification task where images contain orthogonal patches and are learned with a 3-layer overparameterized convolutional network and stochastic gradient descent. We empirically identify a novel phenomenon where the dot-product between the learned pattern detectors and their detected patterns are governed by the pattern statistics in the training set. We call this phenomenon Pattern Statistics Inductive Bias (PSI) and prove that PSI holds for a simple setup with two points in the training set. Furthermore, we prove that if PSI holds, stochastic gradient descent has sample complexity $O(d^2\log(d))$ where $d$ is the filter dimension. In contrast, we show a VC dimension lower bound in our setting which is exponential in $d$. Taken together, our results provide strong evidence that PSI is a unique inductive bias of stochastic gradient descent, that guarantees good generalization properties.

On the Optimality of Trees Generated by ID3

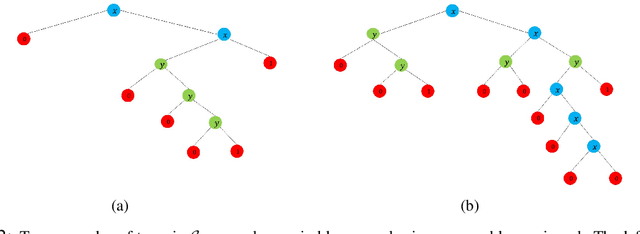
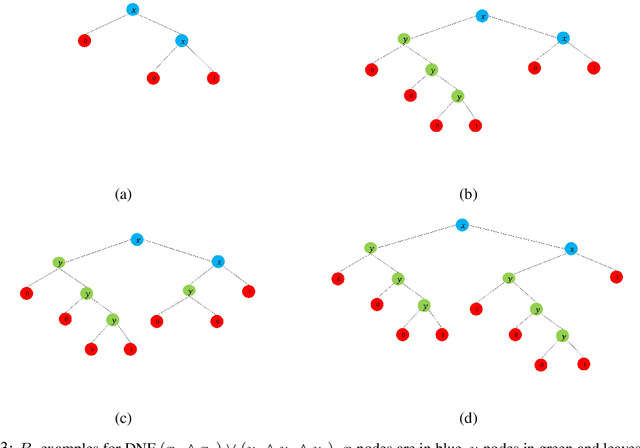
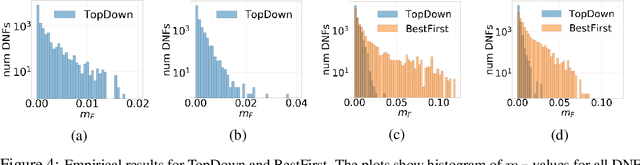
Since its inception in the 1980s, ID3 has become one of the most successful and widely used algorithms for learning decision trees. However, its theoretical properties remain poorly understood. In this work, we analyze the heuristic of growing a decision tree with ID3 for a limited number of iterations $t$ and given that nodes are split as in the case of exact information gain and probability computations. In several settings, we provide theoretical and empirical evidence that the TopDown variant of ID3, introduced by Kearns and Mansour (1996), produces trees with optimal or near-optimal test error among all trees with $t$ internal nodes. We prove optimality in the case of learning conjunctions under product distributions and learning read-once DNFs with 2 terms under the uniform distribition. Using efficient dynamic programming algorithms, we empirically show that TopDown generates trees that are near-optimal ($\sim \%1$ difference from optimal test error) in a large number of settings for learning read-once DNFs under product distributions.

ID3 Learns Juntas for Smoothed Product Distributions

In recent years, there are many attempts to understand popular heuristics. An example of such a heuristic algorithm is the ID3 algorithm for learning decision trees. This algorithm is commonly used in practice, but there are very few theoretical works studying its behavior. In this paper, we analyze the ID3 algorithm, when the target function is a $k$-Junta, a function that depends on $k$ out of $n$ variables of the input. We prove that when $k = \log n$, the ID3 algorithm learns in polynomial time $k$-Juntas, in the smoothed analysis model of Kalai & Teng. That is, we show a learnability result when the observed distribution is a "noisy" variant of the original distribution.

Low Latency Privacy Preserving Inference

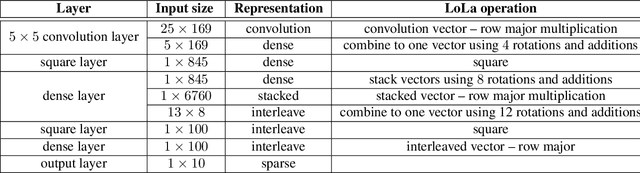
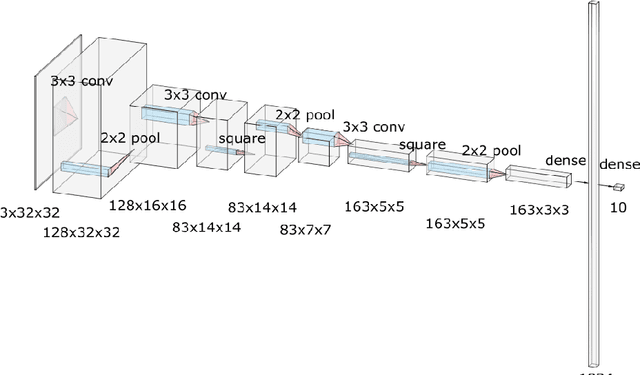
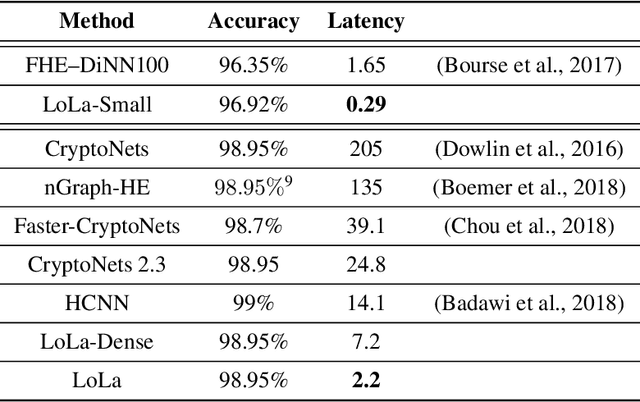
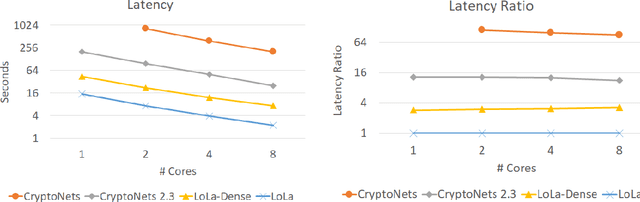
When applying machine learning to sensitive data, one has to balance between accuracy, information leakage, and computational-complexity. Recent studies have shown that Homomorphic Encryption (HE) can be used for protecting against information leakage while applying neural networks. However, this comes with the cost of limiting the width and depth of neural networks that can be used (and hence the accuracy) and with latency of the order of several minutes even for relatively simple networks. In this study we provide two solutions that address these limitations. In the first solution, we present more than $10\times$ improvement in latency and enable inference on wider networks compared to prior attempts with the same level of security. The improved performance is achieved via a collection of methods to better represent the data during the computation. In the second solution, we apply the method of transfer learning to provide private inference services using deep networks with latency less than 0.2 seconds. We demonstrate the efficacy of our methods on several computer vision tasks.

SGD Learns Over-parameterized Networks that Provably Generalize on Linearly Separable Data

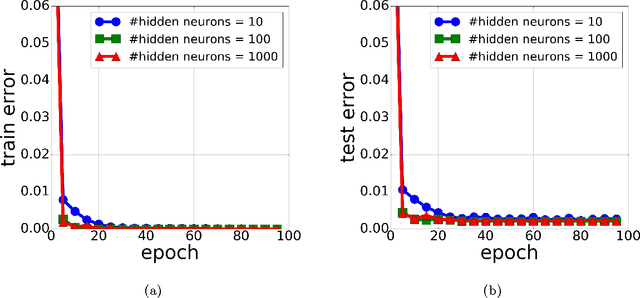
Neural networks exhibit good generalization behavior in the over-parameterized regime, where the number of network parameters exceeds the number of observations. Nonetheless, current generalization bounds for neural networks fail to explain this phenomenon. In an attempt to bridge this gap, we study the problem of learning a two-layer over-parameterized neural network, when the data is generated by a linearly separable function. In the case where the network has Leaky ReLU activations, we provide both optimization and generalization guarantees for over-parameterized networks. Specifically, we prove convergence rates of SGD to a global minimum and provide generalization guarantees for this global minimum that are independent of the network size. Therefore, our result clearly shows that the use of SGD for optimization both finds a global minimum, and avoids overfitting despite the high capacity of the model. This is the first theoretical demonstration that SGD can avoid overfitting, when learning over-specified neural network classifiers.

Globally Optimal Gradient Descent for a ConvNet with Gaussian Inputs

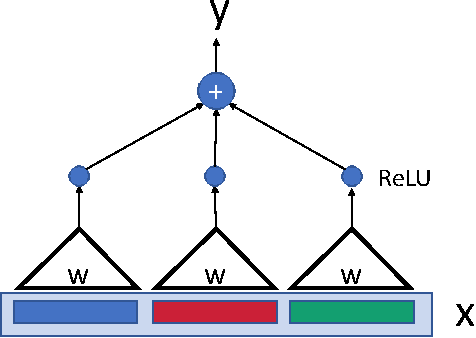
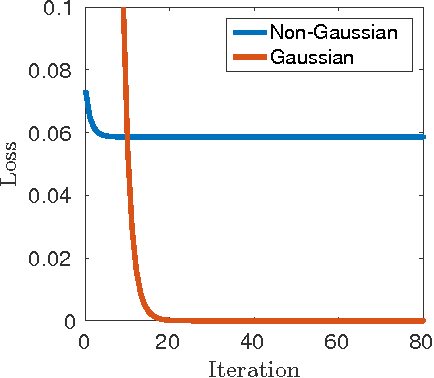
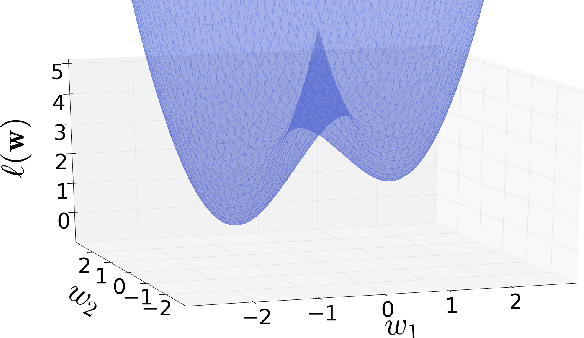
Deep learning models are often successfully trained using gradient descent, despite the worst case hardness of the underlying non-convex optimization problem. The key question is then under what conditions can one prove that optimization will succeed. Here we provide a strong result of this kind. We consider a neural net with one hidden layer and a convolutional structure with no overlap and a ReLU activation function. For this architecture we show that learning is NP-complete in the general case, but that when the input distribution is Gaussian, gradient descent converges to the global optimum in polynomial time. To the best of our knowledge, this is the first global optimality guarantee of gradient descent on a convolutional neural network with ReLU activations.