DeepVL: Dynamics and Inertial Measurements-based Deep Velocity Learning for Underwater Odometry

This paper presents a learned model to predict the robot-centric velocity of an underwater robot through dynamics-aware proprioception. The method exploits a recurrent neural network using as inputs inertial cues, motor commands, and battery voltage readings alongside the hidden state of the previous time-step to output robust velocity estimates and their associated uncertainty. An ensemble of networks is utilized to enhance the velocity and uncertainty predictions. Fusing the network's outputs into an Extended Kalman Filter, alongside inertial predictions and barometer updates, the method enables long-term underwater odometry without further exteroception. Furthermore, when integrated into visual-inertial odometry, the method assists in enhanced estimation resilience when dealing with an order of magnitude fewer total features tracked (as few as 1) as compared to conventional visual-inertial systems. Tested onboard an underwater robot deployed both in a laboratory pool and the Trondheim Fjord, the method takes less than 5ms for inference either on the CPU or the GPU of an NVIDIA Orin AGX and demonstrates less than 4% relative position error in novel trajectories during complete visual blackout, and approximately 2% relative error when a maximum of 2 visual features from a monocular camera are available.

Online Refractive Camera Model Calibration in Visual Inertial Odometry

This paper presents a general refractive camera model and online co-estimation of odometry and the refractive index of unknown media. This enables operation in diverse and varying refractive fluids, given only the camera calibration in air. The refractive index is estimated online as a state variable of a monocular visual-inertial odometry framework in an iterative formulation using the proposed camera model. The method was verified on data collected using an underwater robot traversing inside a pool. The evaluations demonstrate convergence to the ideal refractive index for water despite significant perturbations in the initialization. Simultaneously, the approach enables on-par visual-inertial odometry performance in refractive media without prior knowledge of the refractive index or requirement of medium-specific camera calibration.

An Online Self-calibrating Refractive Camera Model with Application to Underwater Odometry

This work presents a camera model for refractive media such as water and its application in underwater visual-inertial odometry. The model is self-calibrating in real-time and is free of known correspondences or calibration targets. It is separable as a distortion model (dependent on refractive index $n$ and radial pixel coordinate) and a virtual pinhole model (as a function of $n$). We derive the self-calibration formulation leveraging epipolar constraints to estimate the refractive index and subsequently correct for distortion. Through experimental studies using an underwater robot integrating cameras and inertial sensing, the model is validated regarding the accurate estimation of the refractive index and its benefits for robust odometry estimation in an extended envelope of conditions. Lastly, we show the transition between media and the estimation of the varying refractive index online, thus allowing computer vision tasks across refractive media.

Constant-Factor Approximation Algorithms for Socially Fair $k$-Clustering

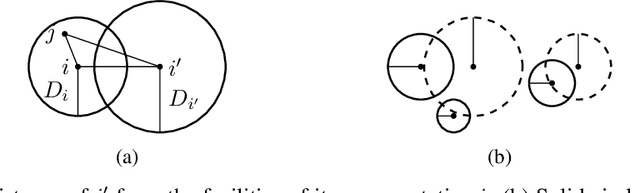
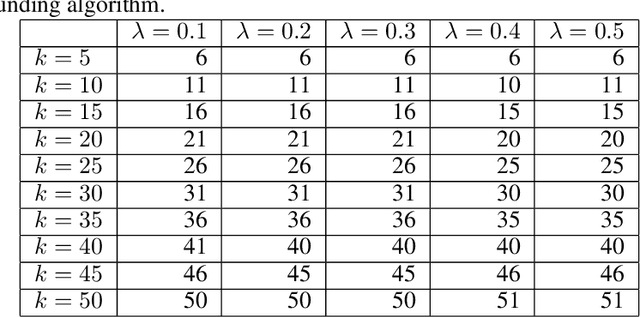
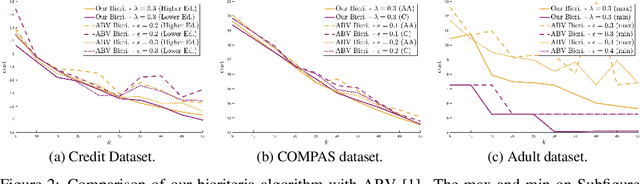
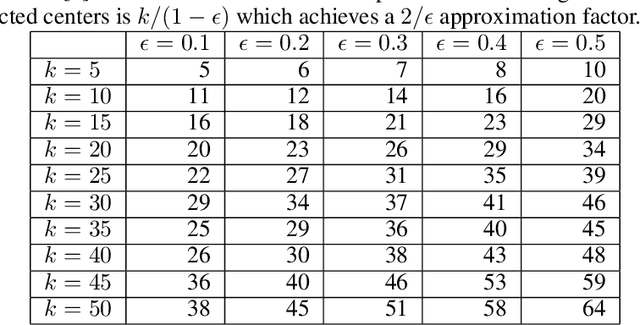
We study approximation algorithms for the socially fair $(\ell_p, k)$-clustering problem with $m$ groups, whose special cases include the socially fair $k$-median ($p=1$) and socially fair $k$-means ($p=2$) problems. We present (1) a polynomial-time $(5+2\sqrt{6})^p$-approximation with at most $k+m$ centers (2) a $(5+2\sqrt{6}+\epsilon)^p$-approximation with $k$ centers in time $n^{2^{O(p)}\cdot m^2}$, and (3) a $(15+6\sqrt{6})^p$ approximation with $k$ centers in time $k^{m}\cdot\text{poly}(n)$. The first result is obtained via a refinement of the iterative rounding method using a sequence of linear programs. The latter two results are obtained by converting a solution with up to $k+m$ centers to one with $k$ centers using sparsification methods for (2) and via an exhaustive search for (3). We also compare the performance of our algorithms with existing bicriteria algorithms as well as exactly $k$ center approximation algorithms on benchmark datasets, and find that our algorithms also outperform existing methods in practice.

Maximizing Determinants under Matroid Constraints

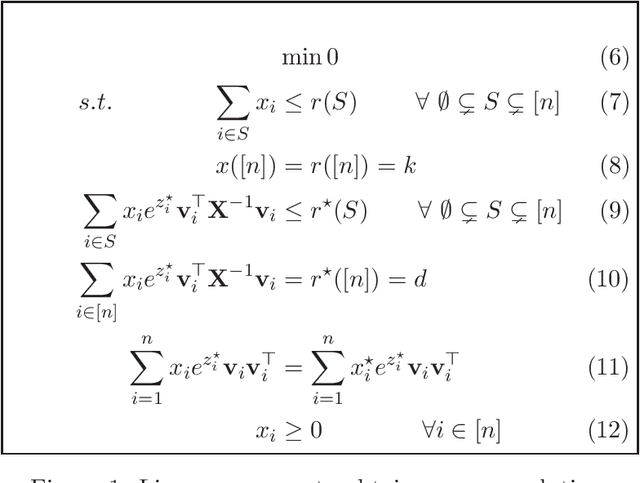
Given vectors $v_1,\dots,v_n\in\mathbb{R}^d$ and a matroid $M=([n],I)$, we study the problem of finding a basis $S$ of $M$ such that $\det(\sum_{i \in S}v_i v_i^\top)$ is maximized. This problem appears in a diverse set of areas such as experimental design, fair allocation of goods, network design, and machine learning. The current best results include an $e^{2k}$-estimation for any matroid of rank $k$ and a $(1+\epsilon)^d$-approximation for a uniform matroid of rank $k\ge d+\frac d\epsilon$, where the rank $k\ge d$ denotes the desired size of the optimal set. Our main result is a new approximation algorithm with an approximation guarantee that depends only on the dimension $d$ of the vectors and not on the size $k$ of the output set. In particular, we show an $(O(d))^{d}$-estimation and an $(O(d))^{d^3}$-approximation for any matroid, giving a significant improvement over prior work when $k\gg d$. Our result relies on the existence of an optimal solution to a convex programming relaxation for the problem which has sparse support; in particular, no more than $O(d^2)$ variables of the solution have fractional values. The sparsity results rely on the interplay between the first-order optimality conditions for the convex program and matroid theory. We believe that the techniques introduced to show sparsity of optimal solutions to convex programs will be of independent interest. We also give a randomized algorithm that rounds a sparse fractional solution to a feasible integral solution to the original problem. To show the approximation guarantee, we utilize recent works on strongly log-concave polynomials and show new relationships between different convex programs studied for the problem. Finally, we use the estimation algorithm and sparsity results to give an efficient deterministic approximation algorithm with an approximation guarantee that depends solely on the dimension $d$.

Fair Dimensionality Reduction and Iterative Rounding for SDPs

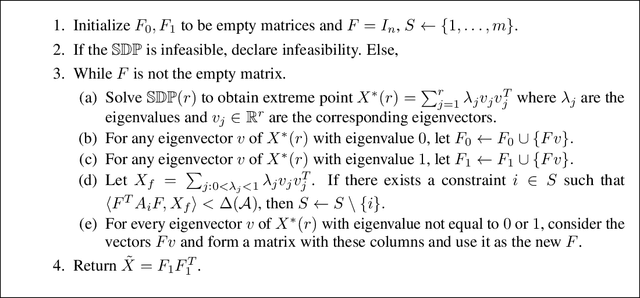
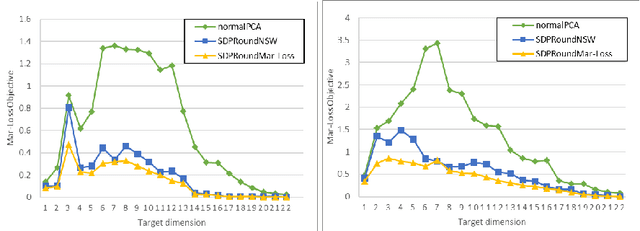
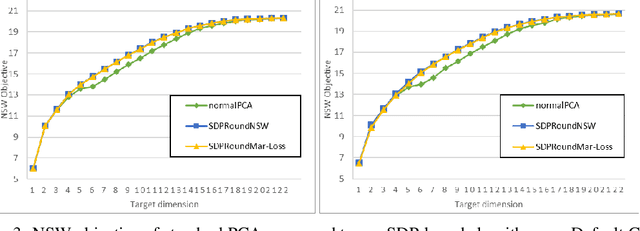
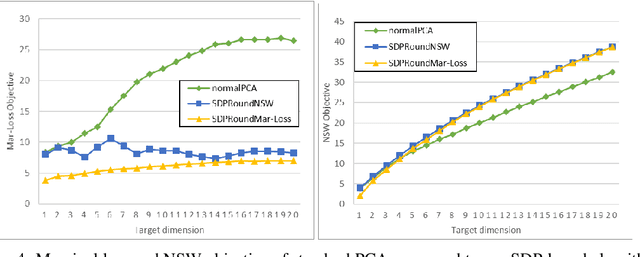
We model "fair" dimensionality reduction as an optimization problem. A central example is the fair PCA problem: the input data is divided into $k$ groups, and the goal is to find a single $d$-dimensional representation for all groups for which the maximum variance (or minimum reconstruction error) is optimized for all groups in a fair (or balanced) manner, e.g., by maximizing the minimum variance over the $k$ groups of the projection to a $d$-dimensional subspace. This problem was introduced by Samadi et al. (2018) who gave a polynomial-time algorithm which, for $k=2$ groups, returns a $(d+1)$-dimensional solution of value at least the best $d$-dimensional solution. We give an exact polynomial-time algorithm for $k=2$ groups. The result relies on extending results of Pataki (1998) regarding rank of extreme point solutions to semi-definite programs. This approach applies more generally to any monotone concave function of the individual group objectives. For $k>2$ groups, our results generalize to give a $(d+\sqrt{2k+0.25}-1.5)$-dimensional solution with objective value as good as the optimal $d$-dimensional solution for arbitrary $k,d$ in polynomial time. Using our extreme point characterization result for SDPs, we give an iterative rounding framework for general SDPs which generalizes the well-known iterative rounding approach for LPs. It returns low-rank solutions with bounded violation of constraints. We obtain a $d$-dimensional projection where the violation in the objective can be bounded additively in terms of the top $O(\sqrt{k})$-singular values of the data matrices. We also give an exact polynomial-time algorithm for any fixed number of groups and target dimension via the algorithm of Grigoriev and Pasechnik (2005). In contrast, when the number of groups is part of the input, even for target dimension $d=1$, we show this problem is NP-hard.

The Price of Fair PCA: One Extra Dimension

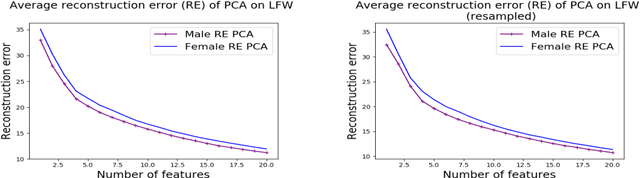
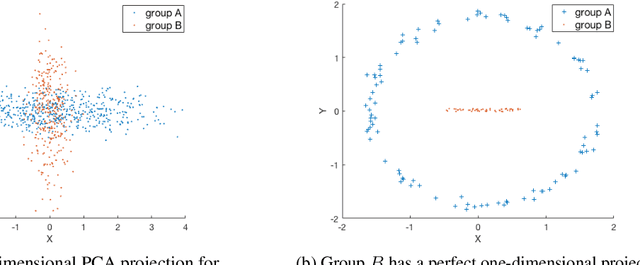
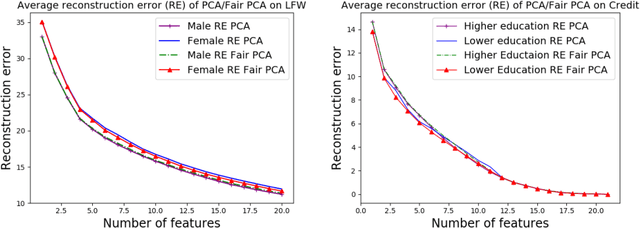
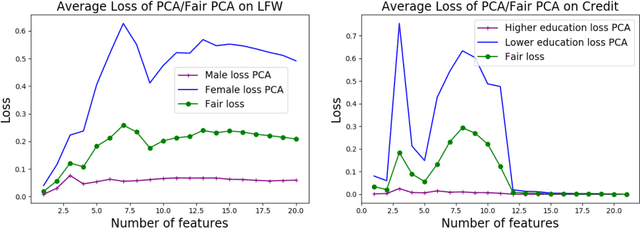
We investigate whether the standard dimensionality reduction technique of PCA inadvertently produces data representations with different fidelity for two different populations. We show on several real-world data sets, PCA has higher reconstruction error on population A than on B (for example, women versus men or lower- versus higher-educated individuals). This can happen even when the data set has a similar number of samples from A and B. This motivates our study of dimensionality reduction techniques which maintain similar fidelity for A and B. We define the notion of Fair PCA and give a polynomial-time algorithm for finding a low dimensional representation of the data which is nearly-optimal with respect to this measure. Finally, we show on real-world data sets that our algorithm can be used to efficiently generate a fair low dimensional representation of the data.

Efficient algorithms for robust submodular maximization under matroid constraints

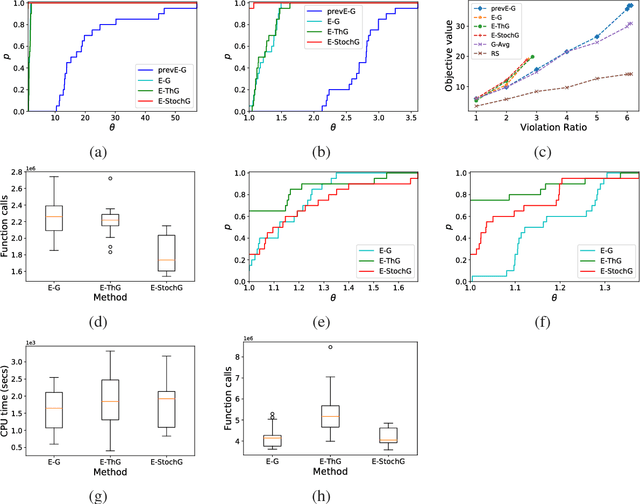
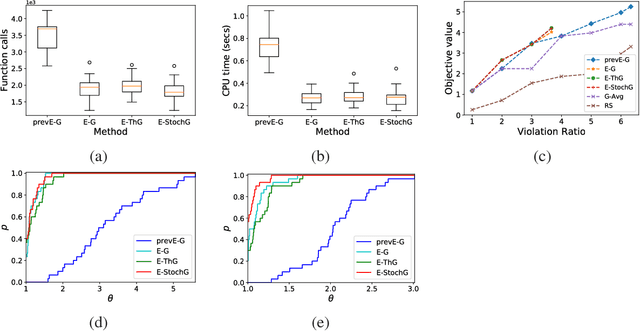
In this work, we consider robust submodular maximization with matroid constraints. We give an efficient bi-criteria approximation algorithm that outputs a small family of feasible sets whose union has (nearly) optimal objective value. This algorithm theoretically performs less function calls than previous works at cost of adding more elements to the final solution. We also provide significant implementation improvements showing that our algorithm outperforms the algorithms in the existing literature. We finally assess the performance of our contributions in three real-world applications.

Proportional Volume Sampling and Approximation Algorithms for A-Optimal Design

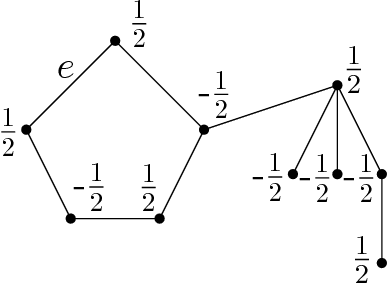
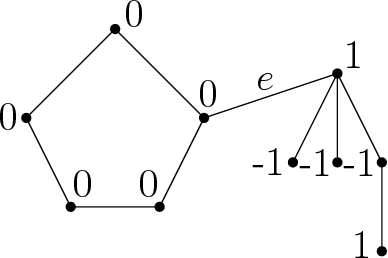
We study the optimal design problems where the goal is to choose a set of linear measurements to obtain the most accurate estimate of an unknown vector in $d$ dimensions. We study the $A$-optimal design variant where the objective is to minimize the average variance of the error in the maximum likelihood estimate of the vector being measured. The problem also finds applications in sensor placement in wireless networks, sparse least squares regression, feature selection for $k$-means clustering, and matrix approximation. In this paper, we introduce proportional volume sampling to obtain improved approximation algorithms for $A$-optimal design. Our main result is to obtain improved approximation algorithms for the $A$-optimal design problem by introducing the proportional volume sampling algorithm. Our results nearly optimal bounds in the asymptotic regime when the number of measurements done, $k$, is significantly more than the dimension $d$. We also give first approximation algorithms when $k$ is small including when $k=d$. The proportional volume-sampling algorithm also gives approximation algorithms for other optimal design objectives such as $D$-optimal design and generalized ratio objective matching or improving previous best known results. Interestingly, we show that a similar guarantee cannot be obtained for the $E$-optimal design problem. We also show that the $A$-optimal design problem is NP-hard to approximate within a fixed constant when $k=d$.

Approximate Positively Correlated Distributions and Approximation Algorithms for D-optimal Design

Experimental design is a classical problem in statistics and has also found new applications in machine learning. In the experimental design problem, the aim is to estimate an unknown vector x in m-dimensions from linear measurements where a Gaussian noise is introduced in each measurement. The goal is to pick k out of the given n experiments so as to make the most accurate estimate of the unknown parameter x. Given a set S of chosen experiments, the most likelihood estimate x' can be obtained by a least squares computation. One of the robust measures of error estimation is the D-optimality criterion which aims to minimize the generalized variance of the estimator. This corresponds to minimizing the volume of the standard confidence ellipsoid for the estimation error x-x'. The problem gives rise to two natural variants depending on whether repetitions are allowed or not. The latter variant, while being more general, has also found applications in the geographical location of sensors. In this work, we first show that a 1/e-approximation for the D-optimal design problem with and without repetitions giving us the first constant factor approximation for the problem. We also consider the case when the number of experiments chosen is much larger than the dimension of the measurements and provide an asymptotically optimal approximation algorithm.