Rewiring with Positional Encodings for Graph Neural Networks

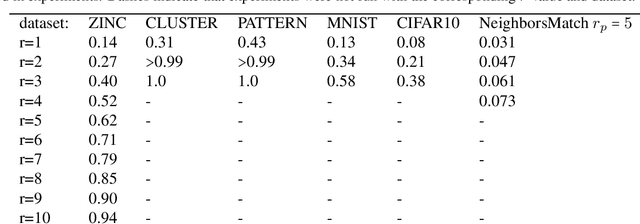
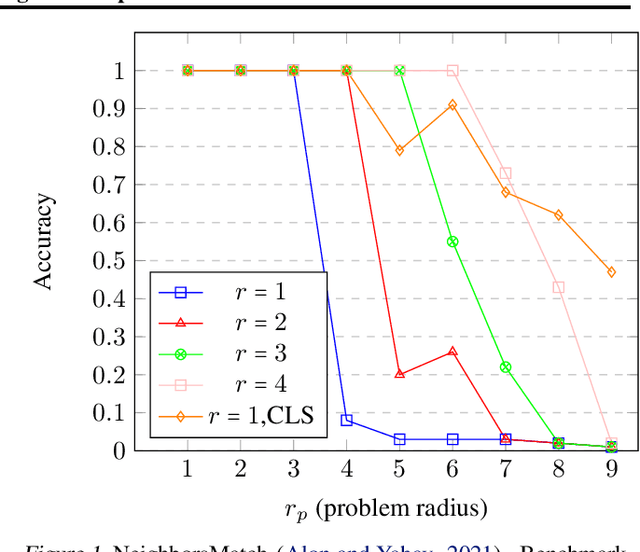
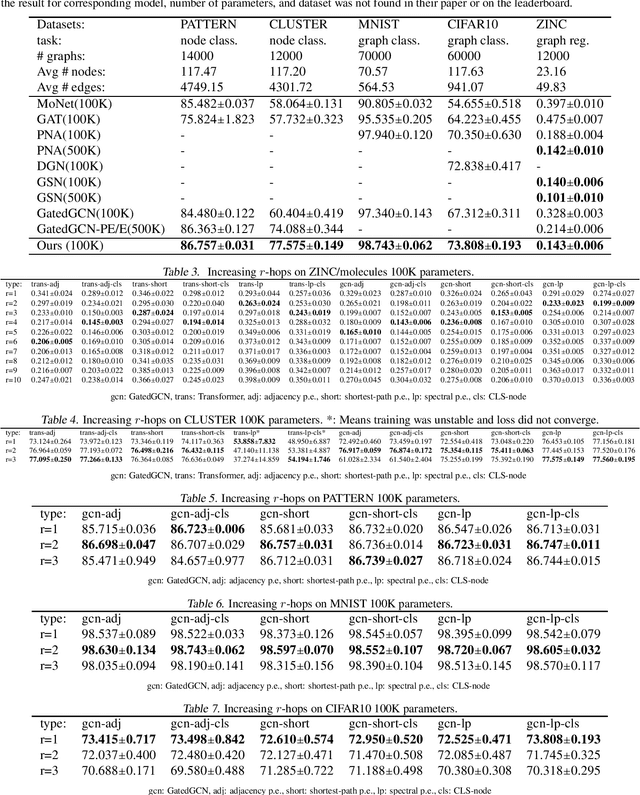
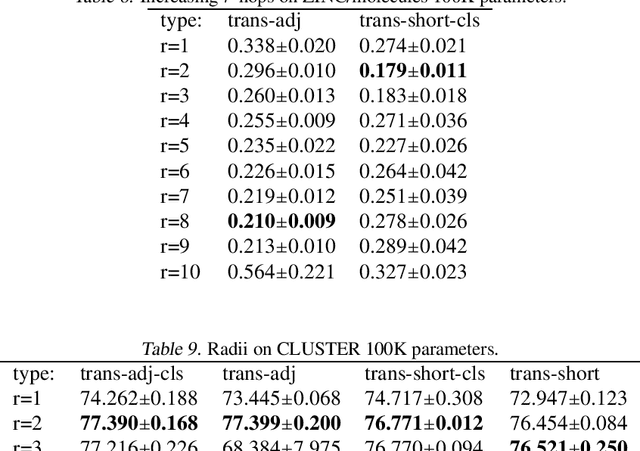
Several recent works use positional encodings to extend the receptive fields of graph neural network (GNN) layers equipped with attention mechanisms. These techniques, however, extend receptive fields to the complete graph, at substantial computational cost and risking a change in the inductive biases of conventional GNNs, or require complex architecture adjustments. As a conservative alternative, we use positional encodings to expand receptive fields to any r-ring. Our method augments the input graph with additional nodes/edges and uses positional encodings as node and/or edge features. Thus, it is compatible with many existing GNN architectures. We also provide examples of positional encodings that are non-invasive, i.e., there is a one-to-one map between the original and the modified graphs. Our experiments demonstrate that extending receptive fields via positional encodings and a virtual fully-connected node significantly improves GNN performance and alleviates over-squashing using small r. We obtain improvements across models, showing state-of-the-art performance even using older architectures than recent Transformer models adapted to graphs.

Learning Proximal Operators to Discover Multiple Optima

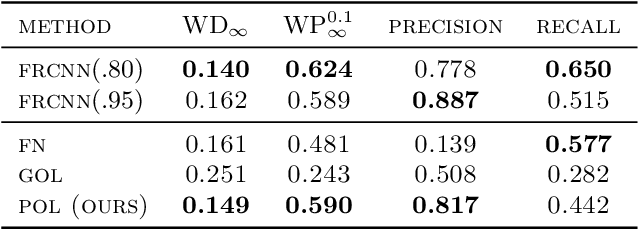
Finding multiple solutions of non-convex optimization problems is a ubiquitous yet challenging task. Typical existing solutions either apply single-solution optimization methods from multiple random initial guesses or search in the vicinity of found solutions using ad hoc heuristics. We present an end-to-end method to learn the proximal operator across a family of non-convex problems, which can then be used to recover multiple solutions for unseen problems at test time. Our method only requires access to the objectives without needing the supervision of ground truth solutions. Notably, the added proximal regularization term elevates the convexity of our formulation: by applying recent theoretical results, we show that for weakly-convex objectives and under mild regularity conditions, training of the proximal operator converges globally in the over-parameterized setting. We further present a benchmark for multi-solution optimization including a wide range of applications and evaluate our method to demonstrate its effectiveness.

On sensitivity of meta-learning to support data

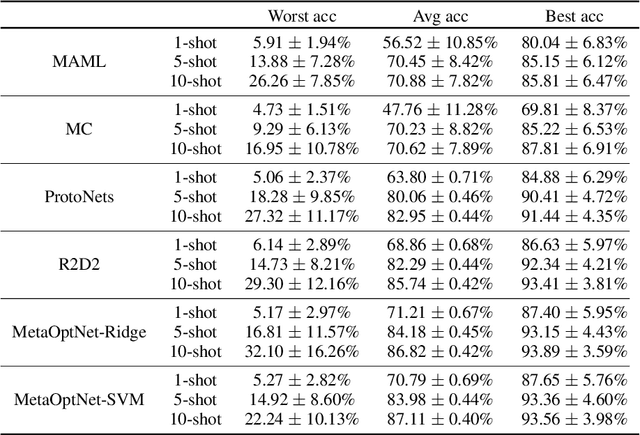
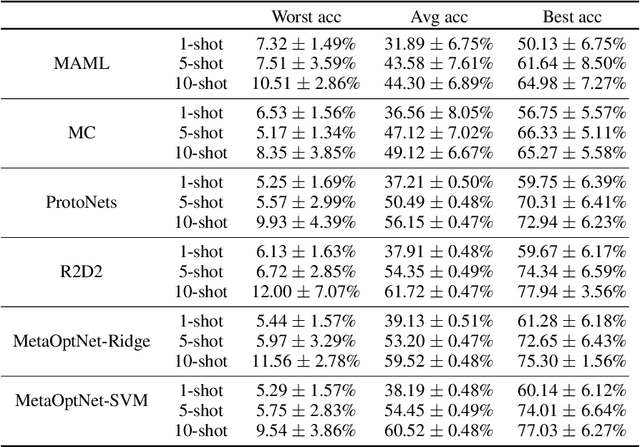
Meta-learning algorithms are widely used for few-shot learning. For example, image recognition systems that readily adapt to unseen classes after seeing only a few labeled examples. Despite their success, we show that modern meta-learning algorithms are extremely sensitive to the data used for adaptation, i.e. support data. In particular, we demonstrate the existence of (unaltered, in-distribution, natural) images that, when used for adaptation, yield accuracy as low as 4\% or as high as 95\% on standard few-shot image classification benchmarks. We explain our empirical findings in terms of class margins, which in turn suggests that robust and safe meta-learning requires larger margins than supervised learning.

Post-processing for Individual Fairness

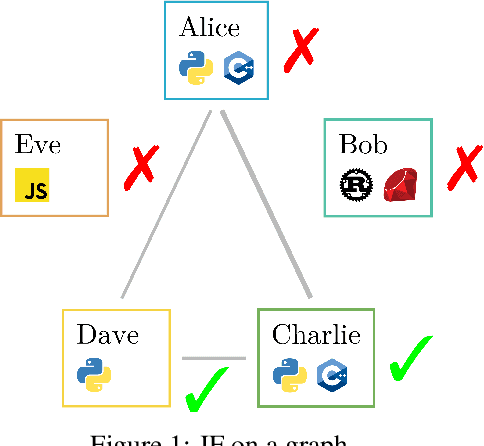
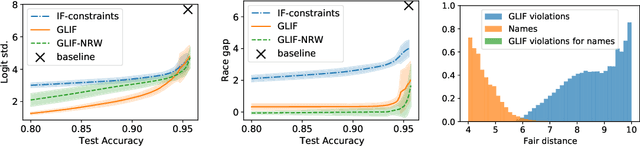
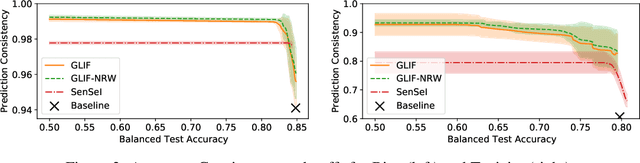
Post-processing in algorithmic fairness is a versatile approach for correcting bias in ML systems that are already used in production. The main appeal of post-processing is that it avoids expensive retraining. In this work, we propose general post-processing algorithms for individual fairness (IF). We consider a setting where the learner only has access to the predictions of the original model and a similarity graph between individuals, guiding the desired fairness constraints. We cast the IF post-processing problem as a graph smoothing problem corresponding to graph Laplacian regularization that preserves the desired "treat similar individuals similarly" interpretation. Our theoretical results demonstrate the connection of the new objective function to a local relaxation of the original individual fairness. Empirically, our post-processing algorithms correct individual biases in large-scale NLP models such as BERT, while preserving accuracy.

Your fairness may vary: Group fairness of pretrained language models in toxic text classification

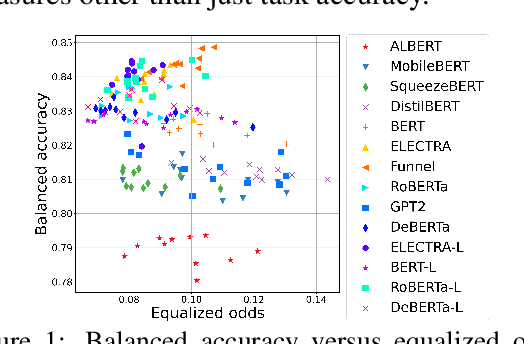
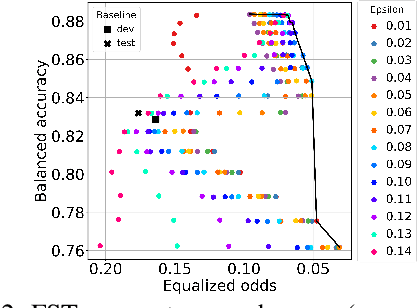
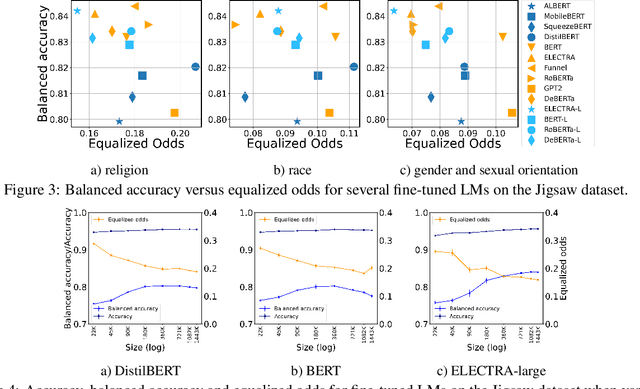
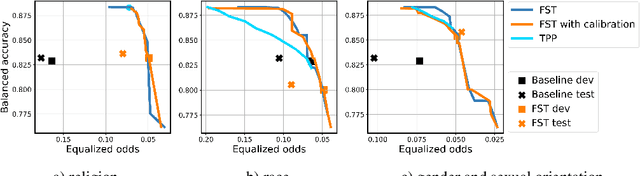
We study the performance-fairness trade-off in more than a dozen fine-tuned LMs for toxic text classification. We empirically show that no blanket statement can be made with respect to the bias of large versus regular versus compressed models. Moreover, we find that focusing on fairness-agnostic performance metrics can lead to models with varied fairness characteristics.

Measuring the sensitivity of Gaussian processes to kernel choice

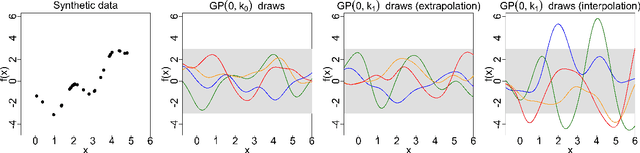
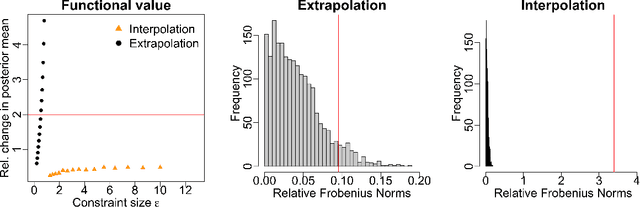
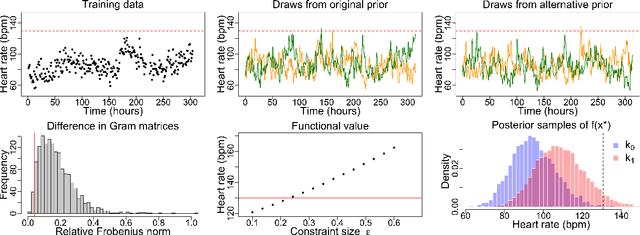
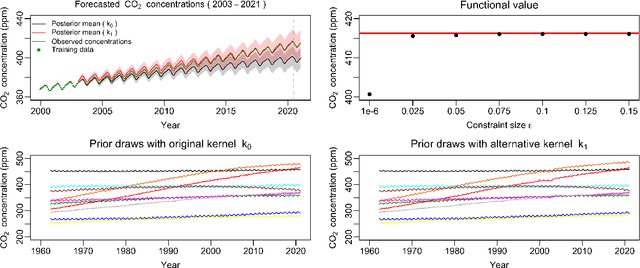
Gaussian processes (GPs) are used to make medical and scientific decisions, including in cardiac care and monitoring of carbon dioxide emissions. But the choice of GP kernel is often somewhat arbitrary. In particular, uncountably many kernels typically align with qualitative prior knowledge (e.g. function smoothness or stationarity). But in practice, data analysts choose among a handful of convenient standard kernels (e.g. squared exponential). In the present work, we ask: Would decisions made with a GP differ under other, qualitatively interchangeable kernels? We show how to formulate this sensitivity analysis as a constrained optimization problem over a finite-dimensional space. We can then use standard optimizers to identify substantive changes in relevant decisions made with a GP. We demonstrate in both synthetic and real-world examples that decisions made with a GP can exhibit substantial sensitivity to kernel choice, even when prior draws are qualitatively interchangeable to a user.

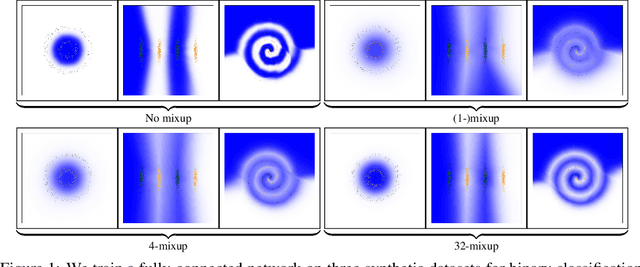
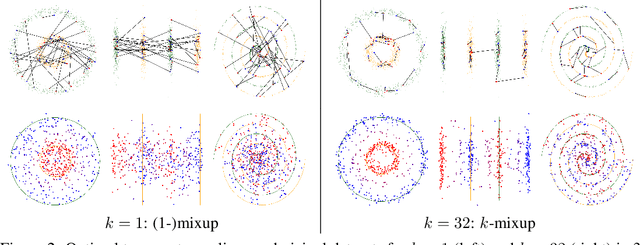
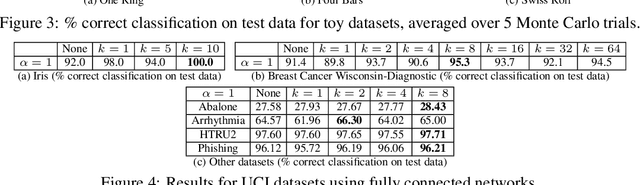
k-Mixup Regularization for Deep Learning via Optimal Transport

Mixup is a popular regularization technique for training deep neural networks that can improve generalization and increase adversarial robustness. It perturbs input training data in the direction of other randomly-chosen instances in the training set. To better leverage the structure of the data, we extend mixup to \emph{$k$-mixup} by perturbing $k$-batches of training points in the direction of other $k$-batches using displacement interpolation, interpolation under the Wasserstein metric. We demonstrate theoretically and in simulations that $k$-mixup preserves cluster and manifold structures, and we extend theory studying efficacy of standard mixup. Our empirical results show that training with $k$-mixup further improves generalization and robustness on benchmark datasets.

Individually Fair Gradient Boosting

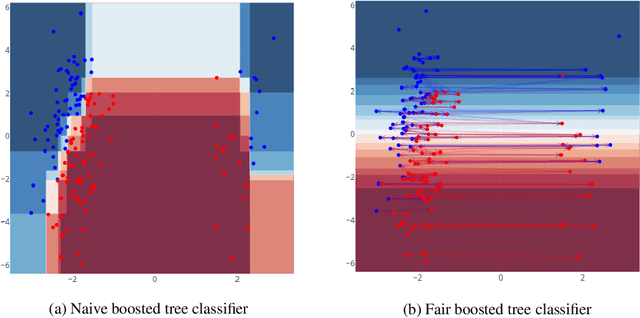
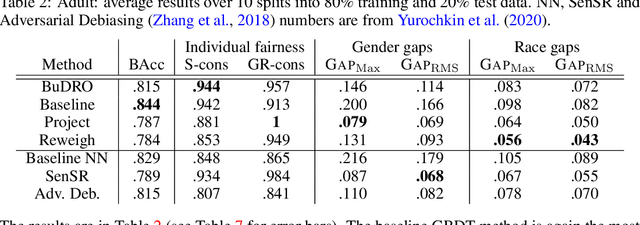
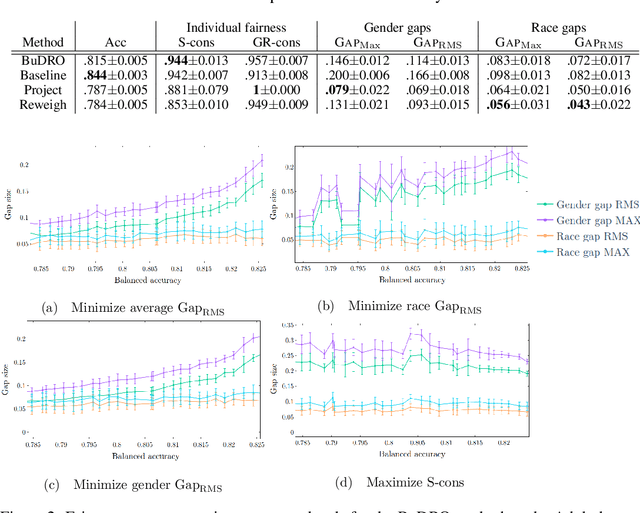
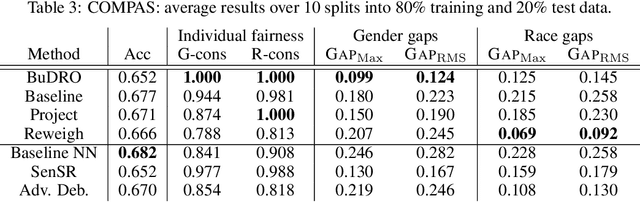
We consider the task of enforcing individual fairness in gradient boosting. Gradient boosting is a popular method for machine learning from tabular data, which arise often in applications where algorithmic fairness is a concern. At a high level, our approach is a functional gradient descent on a (distributionally) robust loss function that encodes our intuition of algorithmic fairness for the ML task at hand. Unlike prior approaches to individual fairness that only work with smooth ML models, our approach also works with non-smooth models such as decision trees. We show that our algorithm converges globally and generalizes. We also demonstrate the efficacy of our algorithm on three ML problems susceptible to algorithmic bias.

Statistical inference for individual fairness

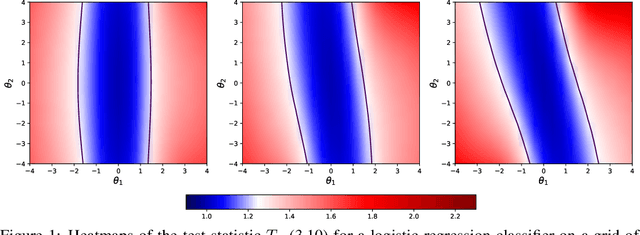
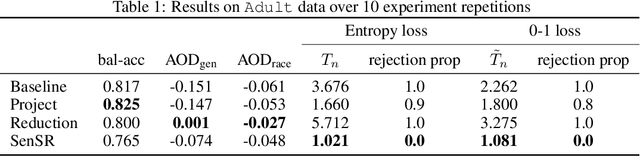
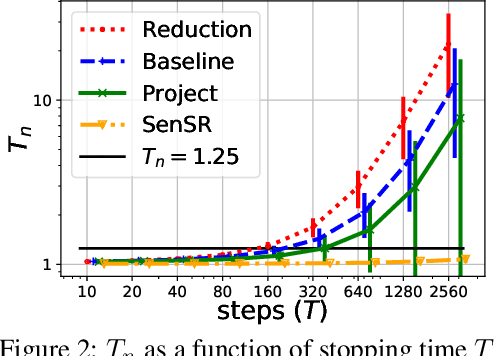
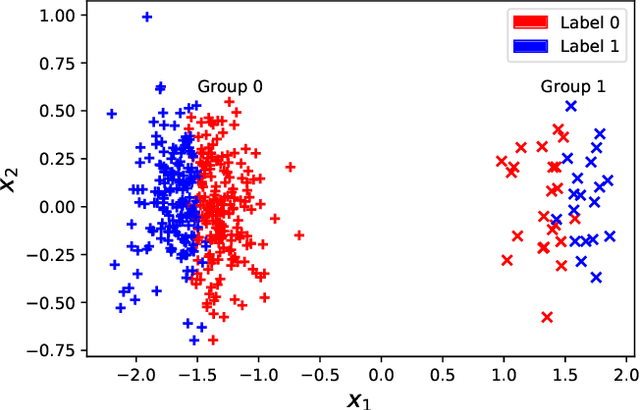
As we rely on machine learning (ML) models to make more consequential decisions, the issue of ML models perpetuating or even exacerbating undesirable historical biases (e.g., gender and racial biases) has come to the fore of the public's attention. In this paper, we focus on the problem of detecting violations of individual fairness in ML models. We formalize the problem as measuring the susceptibility of ML models against a form of adversarial attack and develop a suite of inference tools for the adversarial cost function. The tools allow auditors to assess the individual fairness of ML models in a statistically-principled way: form confidence intervals for the worst-case performance differential between similar individuals and test hypotheses of model fairness with (asymptotic) non-coverage/Type I error rate control. We demonstrate the utility of our tools in a real-world case study.

Individually Fair Ranking

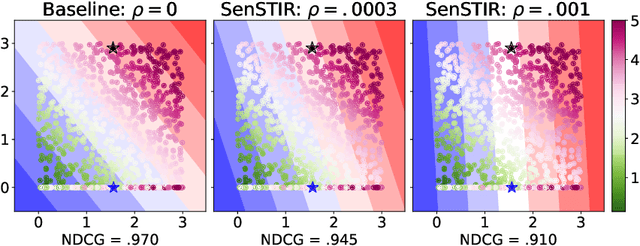
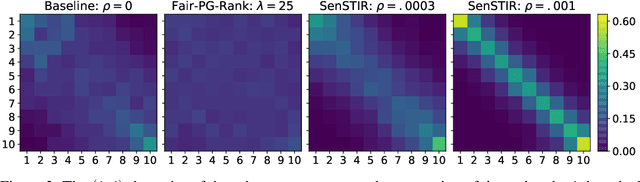
We develop an algorithm to train individually fair learning-to-rank (LTR) models. The proposed approach ensures items from minority groups appear alongside similar items from majority groups. This notion of fair ranking is based on the definition of individual fairness from supervised learning and is more nuanced than prior fair LTR approaches that simply ensure the ranking model provides underrepresented items with a basic level of exposure. The crux of our method is an optimal transport-based regularizer that enforces individual fairness and an efficient algorithm for optimizing the regularizer. We show that our approach leads to certifiably individually fair LTR models and demonstrate the efficacy of our method on ranking tasks subject to demographic biases.