PGLearn -- An Open-Source Learning Toolkit for Optimal Power Flow

Machine Learning (ML) techniques for Optimal Power Flow (OPF) problems have recently garnered significant attention, reflecting a broader trend of leveraging ML to approximate and/or accelerate the resolution of complex optimization problems. These developments are necessitated by the increased volatility and scale in energy production for modern and future grids. However, progress in ML for OPF is hindered by the lack of standardized datasets and evaluation metrics, from generating and solving OPF instances, to training and benchmarking machine learning models. To address this challenge, this paper introduces PGLearn, a comprehensive suite of standardized datasets and evaluation tools for ML and OPF. PGLearn provides datasets that are representative of real-life operating conditions, by explicitly capturing both global and local variability in the data generation, and by, for the first time, including time series data for several large-scale systems. In addition, it supports multiple OPF formulations, including AC, DC, and second-order cone formulations. Standardized datasets are made publicly available to democratize access to this field, reduce the burden of data generation, and enable the fair comparison of various methodologies. PGLearn also includes a robust toolkit for training, evaluating, and benchmarking machine learning models for OPF, with the goal of standardizing performance evaluation across the field. By promoting open, standardized datasets and evaluation metrics, PGLearn aims at democratizing and accelerating research and innovation in machine learning applications for optimal power flow problems. Datasets are available for download at https://www.huggingface.co/PGLearn.

DualSchool: How Reliable are LLMs for Optimization Education?

Consider the following task taught in introductory optimization courses which addresses challenges articulated by the community at the intersection of (generative) AI and OR: generate the dual of a linear program. LLMs, being trained at web-scale, have the conversion process and many instances of Primal to Dual Conversion (P2DC) at their disposal. Students may thus reasonably expect that LLMs would perform well on the P2DC task. To assess this expectation, this paper introduces DualSchool, a comprehensive framework for generating and verifying P2DC instances. The verification procedure of DualSchool uses the Canonical Graph Edit Distance, going well beyond existing evaluation methods for optimization models, which exhibit many false positives and negatives when applied to P2DC. Experiments performed by DualSchool reveal interesting findings. Although LLMs can recite the conversion procedure accurately, state-of-the-art open LLMs fail to consistently produce correct duals. This finding holds even for the smallest two-variable instances and for derivative tasks, such as correctness, verification, and error classification. The paper also discusses the implications for educators, students, and the development of large reasoning systems.

Conformal Prediction with Upper and Lower Bound Models

This paper studies a Conformal Prediction (CP) methodology for building prediction intervals in a regression setting, given only deterministic lower and upper bounds on the target variable. It proposes a new CP mechanism (CPUL) that goes beyond post-processing by adopting a model selection approach over multiple nested interval construction methods. Paradoxically, many well-established CP methods, including CPUL, may fail to provide adequate coverage in regions where the bounds are tight. To remedy this limitation, the paper proposes an optimal thresholding mechanism, OMLT, that adjusts CPUL intervals in tight regions with undercoverage. The combined CPUL-OMLT is validated on large-scale learning tasks where the goal is to bound the optimal value of a parametric optimization problem. The experimental results demonstrate substantial improvements over baseline methods across various datasets.

Dual Interior-Point Optimization Learning

This paper introduces Dual Interior Point Learning (DIPL) and Dual Supergradient Learning (DSL) to learn dual feasible solutions to parametric linear programs with bounded variables, which are pervasive across many industries. DIPL mimics a novel dual interior point algorithm while DSL mimics classical dual supergradient ascent. DIPL and DSL ensure dual feasibility by predicting dual variables associated with the constraints then exploiting the flexibility of the duals of the bound constraints. DIPL and DSL complement existing primal learning methods by providing a certificate of quality. They are shown to produce high-fidelity dual-feasible solutions to large-scale optimal power flow problems providing valid dual bounds under 0.5% optimality gap.

Active Bucketized Learning for ACOPF Optimization Proxies

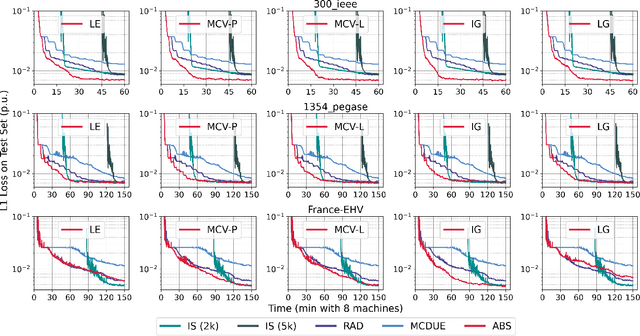
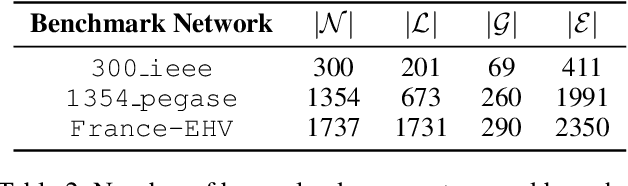
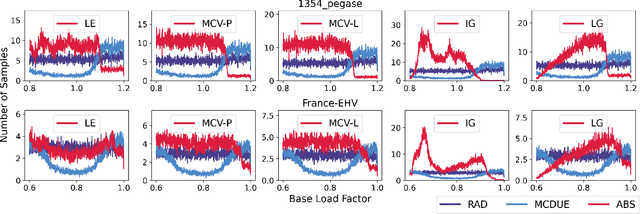
This paper considers optimization proxies for Optimal Power Flow (OPF), i.e., machine-learning models that approximate the input/output relationship of OPF. Recent work has focused on showing that such proxies can be of high fidelity. However, their training requires significant data, each instance necessitating the (offline) solving of an OPF for a sample of the input distribution. To meet the requirements of market-clearing applications, this paper proposes Active Bucketized Sampling (ABS), a novel active learning framework that aims at training the best possible OPF proxy within a time limit. ABS partitions the input distribution into buckets and uses an acquisition function to determine where to sample next. It relies on an adaptive learning rate that increases and decreases over time. Experimental results demonstrate the benefits of ABS.

Risk-Aware Control and Optimization for High-Renewable Power Grids

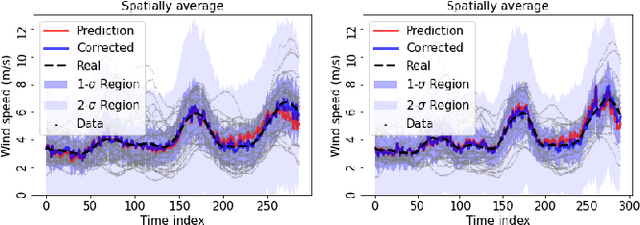
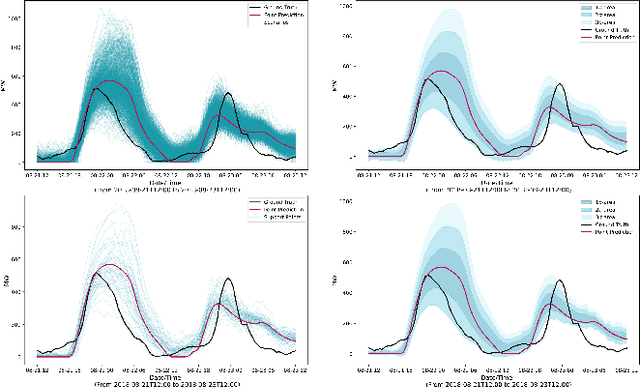
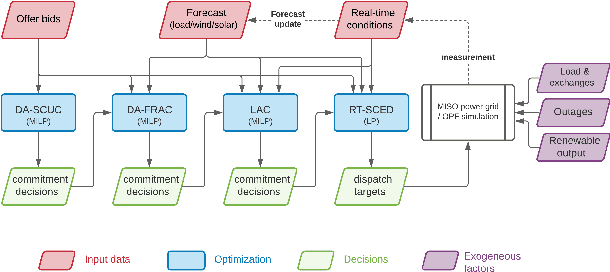
The transition of the electrical power grid from fossil fuels to renewable sources of energy raises fundamental challenges to the market-clearing algorithms that drive its operations. Indeed, the increased stochasticity in load and the volatility of renewable energy sources have led to significant increases in prediction errors, affecting the reliability and efficiency of existing deterministic optimization models. The RAMC project was initiated to investigate how to move from this deterministic setting into a risk-aware framework where uncertainty is quantified explicitly and incorporated in the market-clearing optimizations. Risk-aware market-clearing raises challenges on its own, primarily from a computational standpoint. This paper reviews how RAMC approaches risk-aware market clearing and presents some of its innovations in uncertainty quantification, optimization, and machine learning. Experimental results on real networks are presented.