DualSchool: How Reliable are LLMs for Optimization Education?

Consider the following task taught in introductory optimization courses which addresses challenges articulated by the community at the intersection of (generative) AI and OR: generate the dual of a linear program. LLMs, being trained at web-scale, have the conversion process and many instances of Primal to Dual Conversion (P2DC) at their disposal. Students may thus reasonably expect that LLMs would perform well on the P2DC task. To assess this expectation, this paper introduces DualSchool, a comprehensive framework for generating and verifying P2DC instances. The verification procedure of DualSchool uses the Canonical Graph Edit Distance, going well beyond existing evaluation methods for optimization models, which exhibit many false positives and negatives when applied to P2DC. Experiments performed by DualSchool reveal interesting findings. Although LLMs can recite the conversion procedure accurately, state-of-the-art open LLMs fail to consistently produce correct duals. This finding holds even for the smallest two-variable instances and for derivative tasks, such as correctness, verification, and error classification. The paper also discusses the implications for educators, students, and the development of large reasoning systems.

Compact Optimality Verification for Optimization Proxies

Recent years have witnessed increasing interest in optimization proxies, i.e., machine learning models that approximate the input-output mapping of parametric optimization problems and return near-optimal feasible solutions. Following recent work by (Nellikkath & Chatzivasileiadis, 2021), this paper reconsiders the optimality verification problem for optimization proxies, i.e., the determination of the worst-case optimality gap over the instance distribution. The paper proposes a compact formulation for optimality verification and a gradient-based primal heuristic that brings substantial computational benefits to the original formulation. The compact formulation is also more general and applies to non-convex optimization problems. The benefits of the compact formulation are demonstrated on large-scale DC Optimal Power Flow and knapsack problems.

Just-In-Time Learning for Operational Risk Assessment in Power Grids

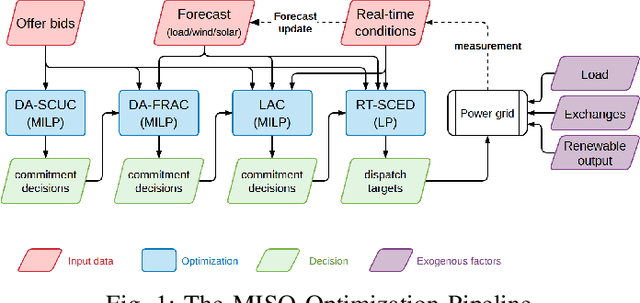
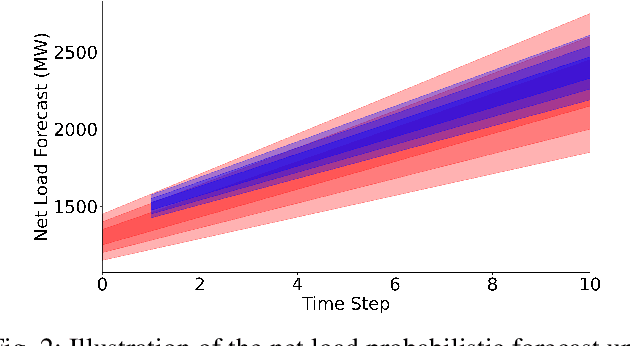
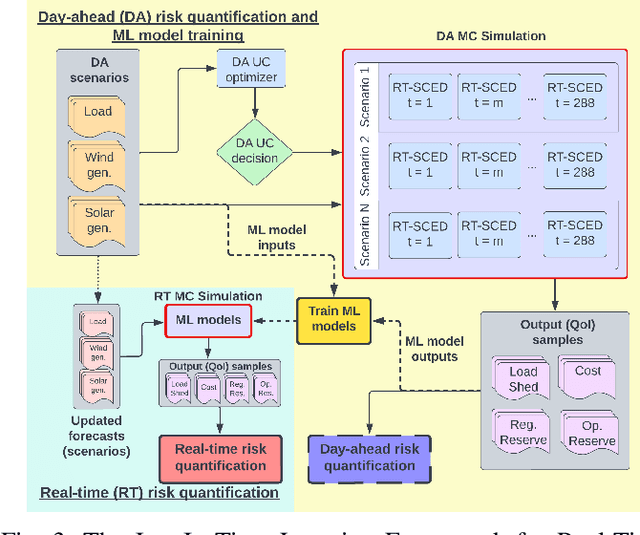
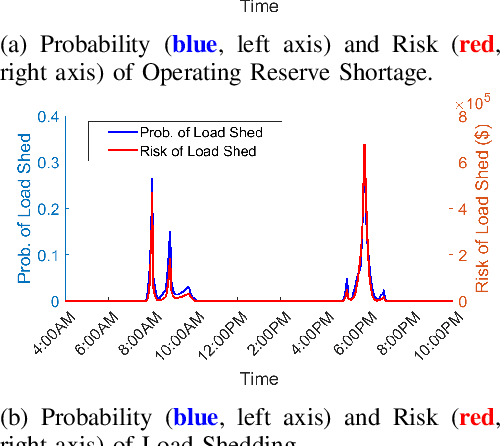
In a grid with a significant share of renewable generation, operators will need additional tools to evaluate the operational risk due to the increased volatility in load and generation. The computational requirements of the forward uncertainty propagation problem, which must solve numerous security-constrained economic dispatch (SCED) optimizations, is a major barrier for such real-time risk assessment. This paper proposes a Just-In-Time Risk Assessment Learning Framework (JITRALF) as an alternative. JITRALF trains risk surrogates, one for each hour in the day, using Machine Learning (ML) to predict the quantities needed to estimate risk, without explicitly solving the SCED problem. This significantly reduces the computational burden of the forward uncertainty propagation and allows for fast, real-time risk estimation. The paper also proposes a novel, asymmetric loss function and shows that models trained using the asymmetric loss perform better than those using symmetric loss functions. JITRALF is evaluated on the French transmission system for assessing the risk of insufficient operating reserves, the risk of load shedding, and the expected operating cost.

Risk-Aware Control and Optimization for High-Renewable Power Grids

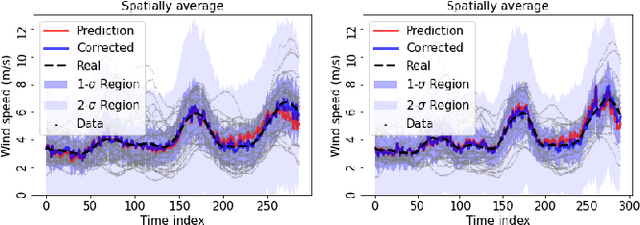
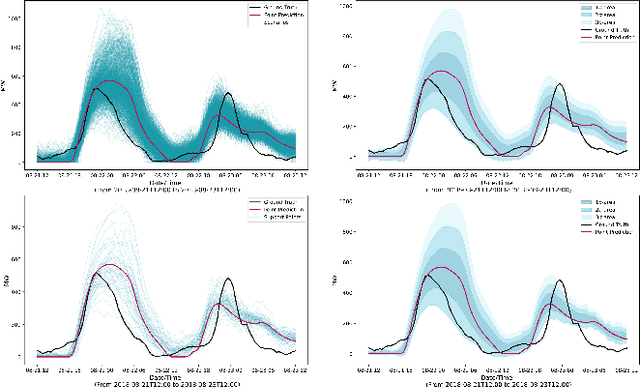
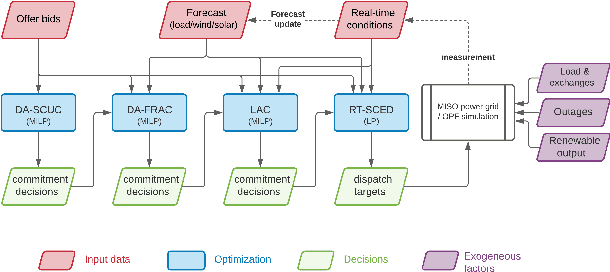
The transition of the electrical power grid from fossil fuels to renewable sources of energy raises fundamental challenges to the market-clearing algorithms that drive its operations. Indeed, the increased stochasticity in load and the volatility of renewable energy sources have led to significant increases in prediction errors, affecting the reliability and efficiency of existing deterministic optimization models. The RAMC project was initiated to investigate how to move from this deterministic setting into a risk-aware framework where uncertainty is quantified explicitly and incorporated in the market-clearing optimizations. Risk-aware market-clearing raises challenges on its own, primarily from a computational standpoint. This paper reviews how RAMC approaches risk-aware market clearing and presents some of its innovations in uncertainty quantification, optimization, and machine learning. Experimental results on real networks are presented.