Knowing The What But Not The Where in Bayesian Optimization

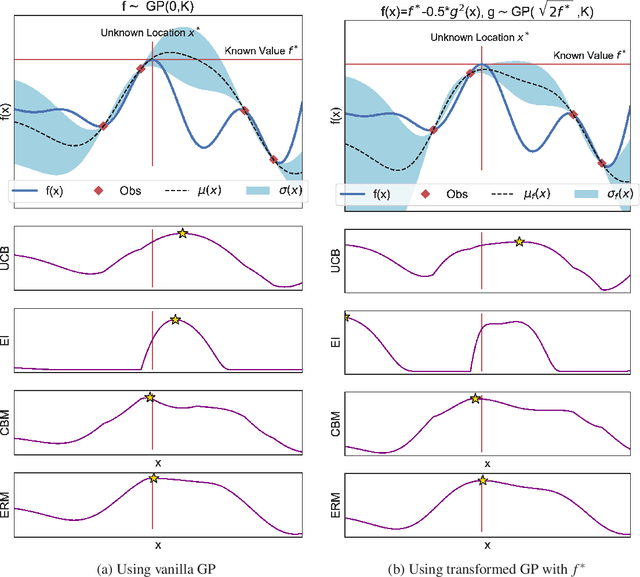
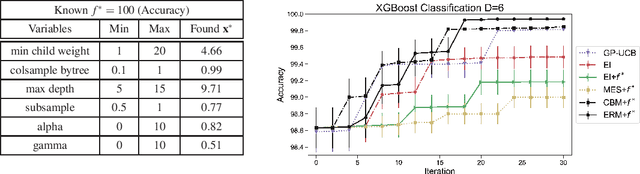
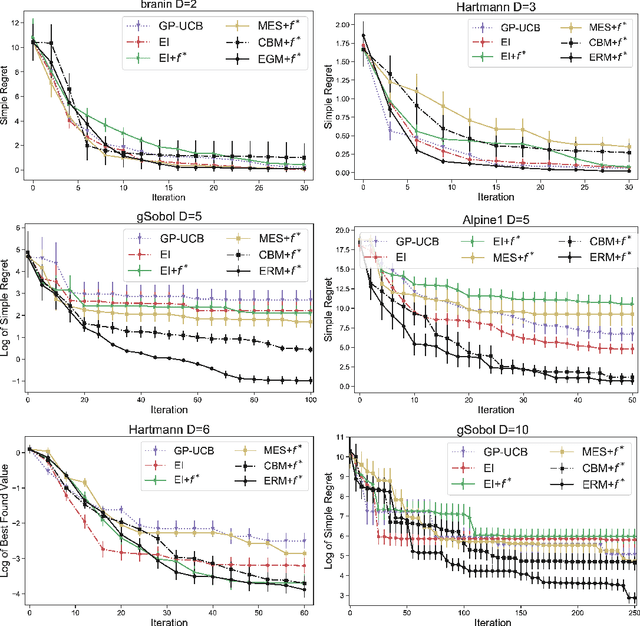
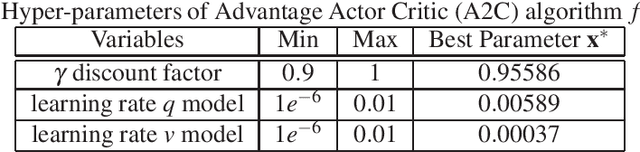
Bayesian optimization has demonstrated impressive success in finding the optimum location $x^{*}$ and value $f^{*}=f(x^{*})=\max_{x\in\mathcal{X}}f(x)$ of the black-box function $f$. In some applications, however, the optimum value is known in advance and the goal is to find the corresponding optimum location. Existing work in Bayesian optimization (BO) has not effectively exploited the knowledge of $f^{*}$ for optimization. In this paper, we consider a new setting in BO in which the knowledge of the optimum value is available. Our goal is to exploit the knowledge about $f^{*}$ to search for the location $x^{*}$ efficiently. To achieve this goal, we first transform the Gaussian process surrogate using the information about the optimum value. Then, we propose two acquisition functions, called confidence bound minimization and expected regret minimization, which exploit the knowledge about the optimum value to identify the optimum location efficiently. We show that our approaches work both intuitively and quantitatively achieve better performance against standard BO methods. We demonstrate real applications in tuning a deep reinforcement learning algorithm on the CartPole problem and XGBoost on Skin Segmentation dataset in which the optimum values are publicly available.

Automated Model Selection with Bayesian Quadrature

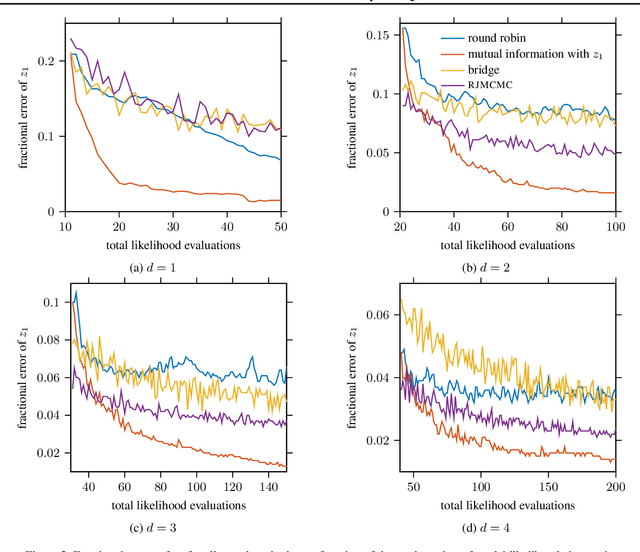
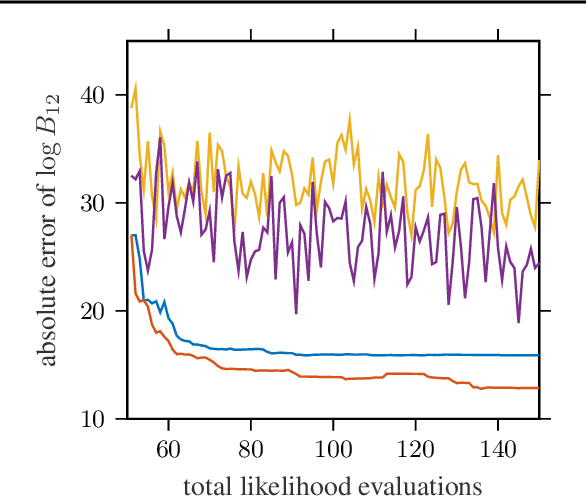
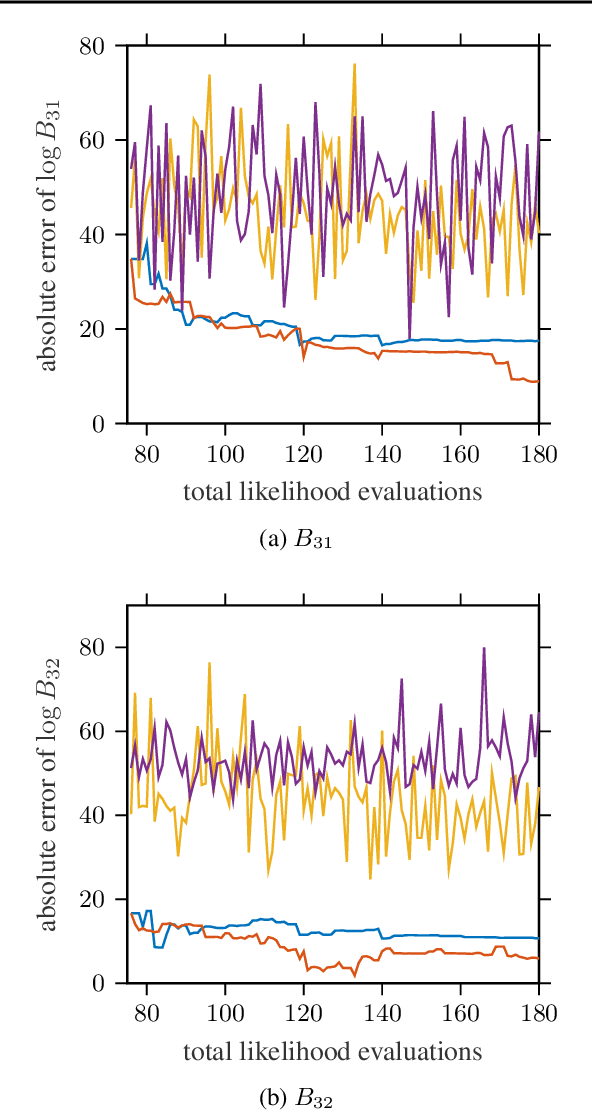
We present a novel technique for tailoring Bayesian quadrature (BQ) to model selection. The state-of-the-art for comparing the evidence of multiple models relies on Monte Carlo methods, which converge slowly and are unreliable for computationally expensive models. Previous research has shown that BQ offers sample efficiency superior to Monte Carlo in computing the evidence of an individual model. However, applying BQ directly to model comparison may waste computation producing an overly-accurate estimate for the evidence of a clearly poor model. We propose an automated and efficient algorithm for computing the most-relevant quantity for model selection: the posterior probability of a model. Our technique maximizes the mutual information between this quantity and observations of the models' likelihoods, yielding efficient acquisition of samples across disparate model spaces when likelihood observations are limited. Our method produces more-accurate model posterior estimates using fewer model likelihood evaluations than standard Bayesian quadrature and Monte Carlo estimators, as we demonstrate on synthetic and real-world examples.

Asynchronous Batch Bayesian Optimisation with Improved Local Penalisation

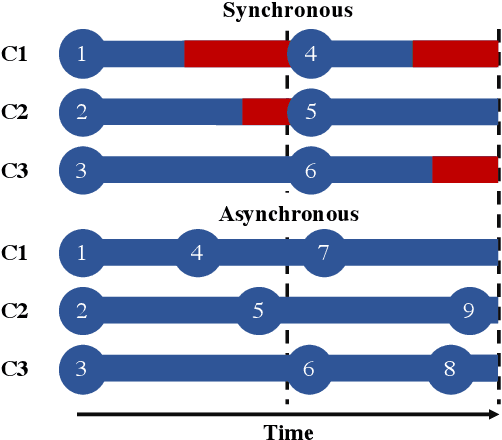
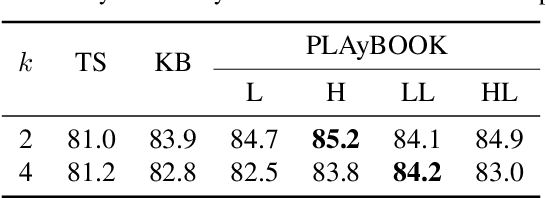
Batch Bayesian optimisation (BO) has been successfully applied to hyperparameter tuning using parallel computing, but it is wasteful of resources: workers that complete jobs ahead of others are left idle. We address this problem by developing an approach, Penalising Locally for Asynchronous Bayesian Optimisation on $k$ workers (PLAyBOOK), for asynchronous parallel BO. We demonstrate empirically the efficacy of PLAyBOOK and its variants on synthetic tasks and a real-world problem. We undertake a comparison between synchronous and asynchronous BO, and show that asynchronous BO often outperforms synchronous batch BO in both wall-clock time and number of function evaluations.

Rejoinder for "Probabilistic Integration: A Role in Statistical Computation?"

This article is the rejoinder for the paper "Probabilistic Integration: A Role in Statistical Computation?" to appear in Statistical Science with discussion. We would first like to thank the reviewers and many of our colleagues who helped shape this paper, the editor for selecting our paper for discussion, and of course all of the discussants for their thoughtful, insightful and constructive comments. In this rejoinder, we respond to some of the points raised by the discussants and comment further on the fundamental questions underlying the paper: (i) Should Bayesian ideas be used in numerical analysis?, and (ii) If so, what role should such approaches have in statistical computation?

Fingerprint Policy Optimisation for Robust Reinforcement Learning

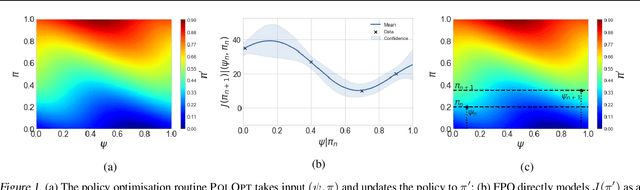
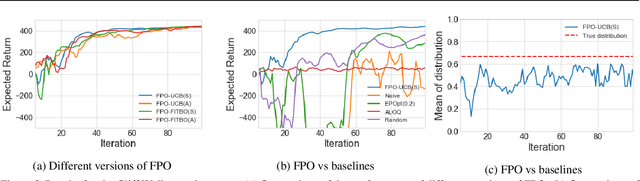
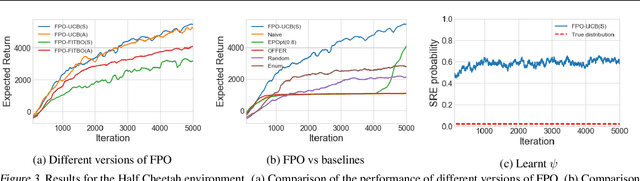
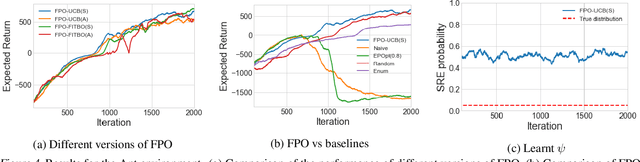
Policy gradient methods have been successfully applied to a variety of reinforcement learning tasks. However, while learning in a simulator, these methods do not utilise the opportunity to improve learning by adjusting certain environment variables: unobservable state features that are randomly determined by the environment in a physical setting, but that are controllable in a simulator. This can lead to slow learning or convergence to highly suboptimal policies if the environment variable has a large impact on the transition dynamics. In this paper, we present fingerprint policy optimisation (FPO) which finds a policy that is optimal in expectation across the distribution of environment variables. The central idea is to use Bayesian optimisation (BO) to actively select the distribution of the environment variable that maximises the improvement generated by each iteration of the policy gradient method. To make this BO practical, we contribute two easy-to-compute low-dimensional fingerprints of the current policy. We apply FPO to a number of continuous control tasks of varying difficulty and show that FPO can efficiently learn policies that are robust to significant rare events, which are unlikely to be observable under random sampling but are key to learning good policies.

Battery health prediction under generalized conditions using a Gaussian process transition model

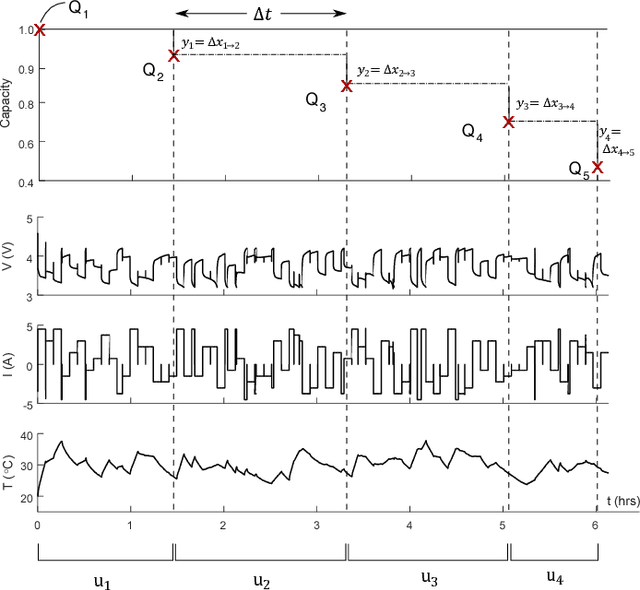
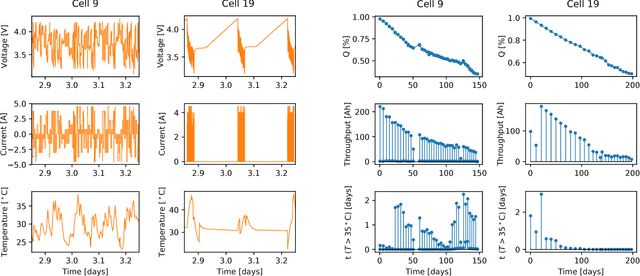
Accurately predicting the future health of batteries is necessary to ensure reliable operation, minimise maintenance costs, and calculate the value of energy storage investments. The complex nature of degradation renders data-driven approaches a promising alternative to mechanistic modelling. This study predicts the changes in battery capacity over time using a Bayesian non-parametric approach based on Gaussian process regression. These changes can be integrated against an arbitrary input sequence to predict capacity fade in a variety of usage scenarios, forming a generalised health model. The approach naturally incorporates varying current, voltage and temperature inputs, crucial for enabling real world application. A key innovation is the feature selection step, where arbitrary length current, voltage and temperature measurement vectors are mapped to fixed size feature vectors, enabling them to be efficiently used as exogenous variables. The approach is demonstrated on the open-source NASA Randomised Battery Usage Dataset, with data of 26 cells aged under randomized operational conditions. Using half of the cells for training, and half for validation, the method is shown to accurately predict non-linear capacity fade, with a best case normalised root mean square error of 4.3%, including accurate estimation of prediction uncertainty.

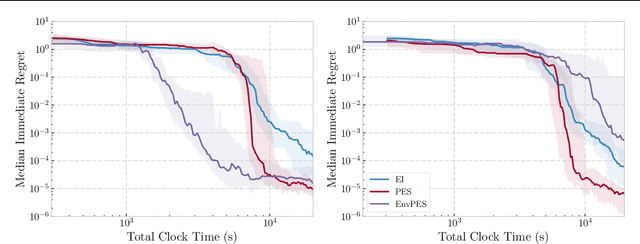
Fast Information-theoretic Bayesian Optimisation

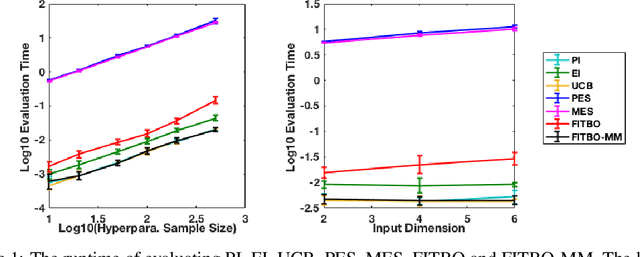
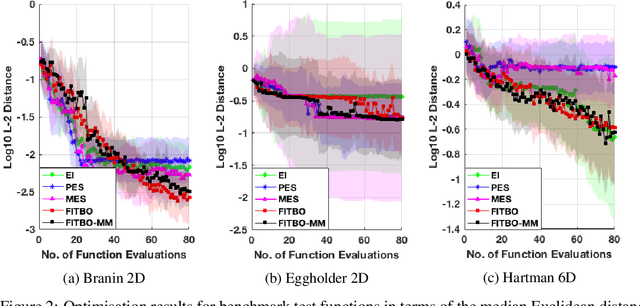
Information-theoretic Bayesian optimisation techniques have demonstrated state-of-the-art performance in tackling important global optimisation problems. However, current information-theoretic approaches require many approximations in implementation, introduce often-prohibitive computational overhead and limit the choice of kernels available to model the objective. We develop a fast information-theoretic Bayesian Optimisation method, FITBO, that avoids the need for sampling the global minimiser, thus significantly reducing computational overhead. Moreover, in comparison with existing approaches, our method faces fewer constraints on kernel choice and enjoys the merits of dealing with the output space. We demonstrate empirically that FITBO inherits the performance associated with information-theoretic Bayesian optimisation, while being even faster than simpler Bayesian optimisation approaches, such as Expected Improvement.

Optimization, fast and slow: optimally switching between local and Bayesian optimization

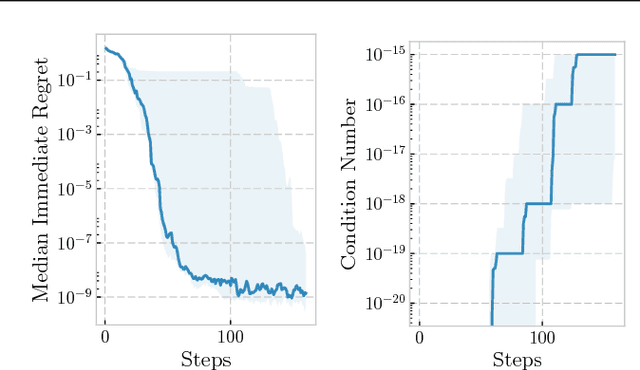
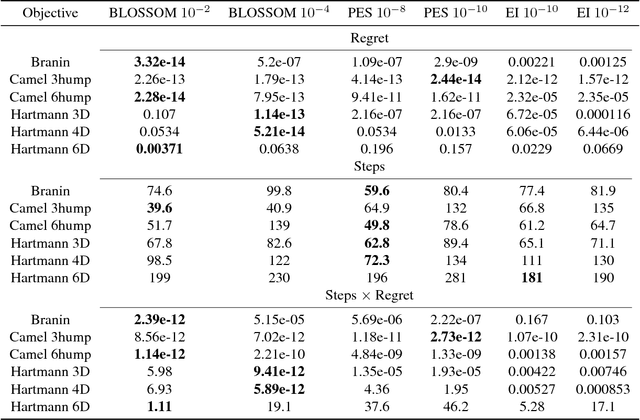
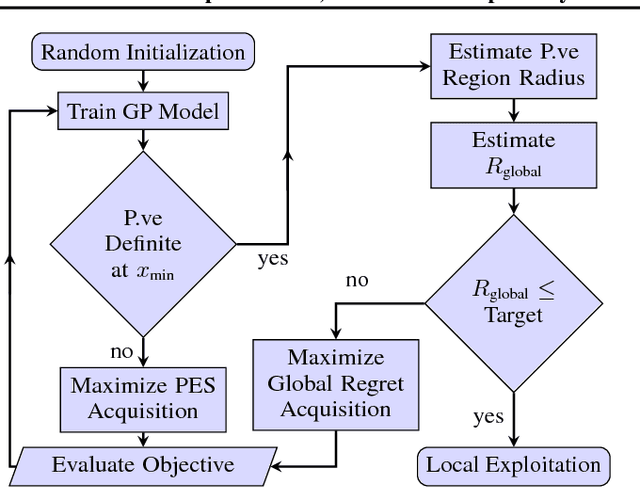
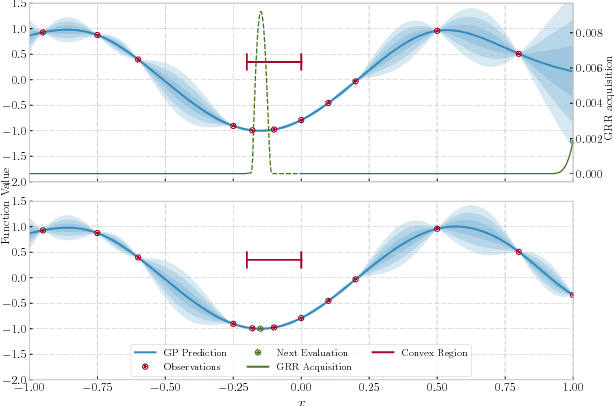
We develop the first Bayesian Optimization algorithm, BLOSSOM, which selects between multiple alternative acquisition functions and traditional local optimization at each step. This is combined with a novel stopping condition based on expected regret. This pairing allows us to obtain the best characteristics of both local and Bayesian optimization, making efficient use of function evaluations while yielding superior convergence to the global minimum on a selection of optimization problems, and also halting optimization once a principled and intuitive stopping condition has been fulfilled.

Practical Bayesian Optimization for Variable Cost Objectives

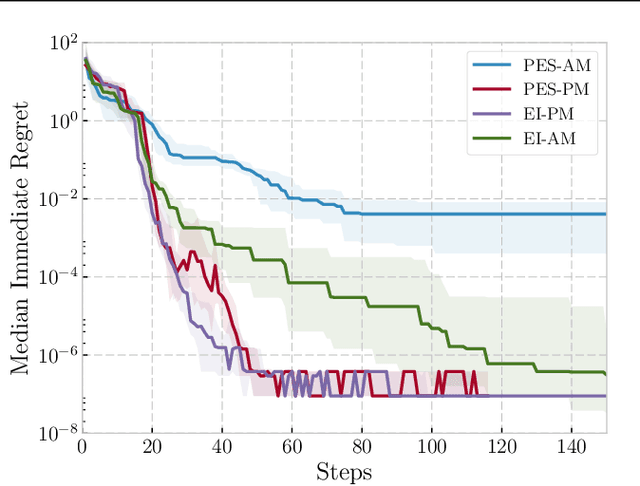
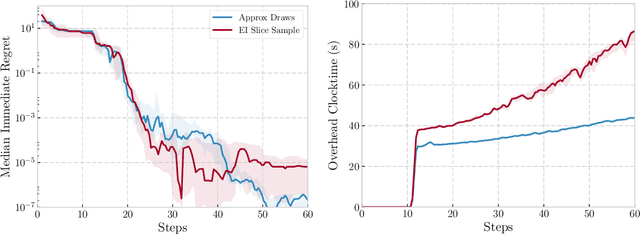
We propose a novel Bayesian Optimization approach for black-box functions with an environmental variable whose value determines the tradeoff between evaluation cost and the fidelity of the evaluations. Further, we use a novel approach to sampling support points, allowing faster construction of the acquisition function. This allows us to achieve optimization with lower overheads than previous approaches and is implemented for a more general class of problem. We show this approach to be effective on synthetic and real world benchmark problems.

Distributionally Ambiguous Optimization Techniques for Batch Bayesian Optimization

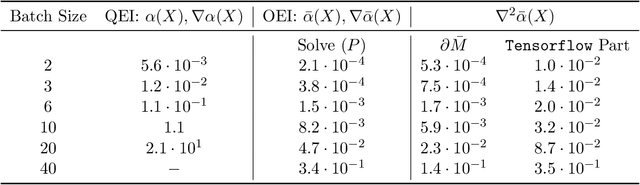
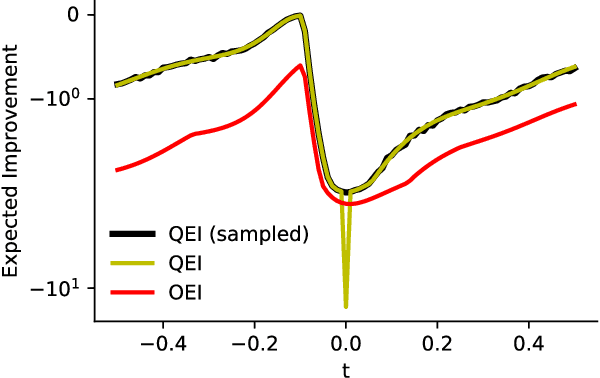
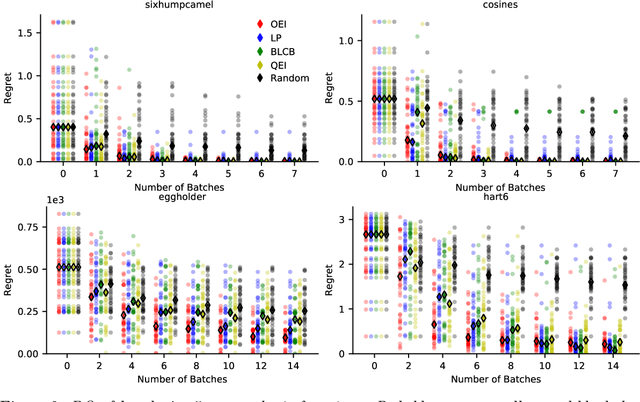
We propose a novel, theoretically-grounded, acquisition function for Batch Bayesian optimization informed by insights from distributionally ambiguous optimization. Our acquisition function is a lower bound on the well-known Expected Improvement function, which requires evaluation of a Gaussian Expectation over a multivariate piecewise affine function. Our bound is computed instead by evaluating the best-case expectation over all probability distributions consistent with the same mean and variance as the original Gaussian distribution. Unlike alternative approaches, including Expected Improvement, our proposed acquisition function avoids multi-dimensional integrations entirely, and can be computed exactly - even on large batch sizes - as the solution of a tractable convex optimization problem. Our suggested acquisition function can also be optimized efficiently, since first and second derivative information can be calculated inexpensively as by-products of the acquisition function calculation itself. We derive various novel theorems that ground our work theoretically and we demonstrate superior performance via simple motivating examples, benchmark functions and real-world problems.