Fine-Grained Bias Exploration and Mitigation for Group-Robust Classification

Achieving group-robust generalization in the presence of spurious correlations remains a significant challenge, particularly when bias annotations are unavailable. Recent studies on Class-Conditional Distribution Balancing (CCDB) reveal that spurious correlations often stem from mismatches between the class-conditional and marginal distributions of bias attributes. They achieve promising results by addressing this issue through simple distribution matching in a bias-agnostic manner. However, CCDB approximates each distribution using a single Gaussian, which is overly simplistic and rarely holds in real-world applications. To address this limitation, we propose a novel method called Bias Exploration via Overfitting (BEO), which captures each distribution in greater detail by modeling it as a mixture of latent groups. Building on these group-level descriptions, we introduce a fine-grained variant of CCDB, termed FG-CCDB, which performs more precise distribution matching and balancing within each group. Through group-level reweighting, FG-CCDB learns sample weights from a global perspective, achieving stronger mitigation of spurious correlations without incurring substantial storage or computational costs. Extensive experiments demonstrate that BEO serves as a strong proxy for ground-truth bias annotations and can be seamlessly integrated with bias-supervised methods. Moreover, when combined with FG-CCDB, our method performs on par with bias-supervised approaches on binary classification tasks and significantly outperforms them in highly biased multi-class scenarios.

Class-Conditional Distribution Balancing for Group Robust Classification

Spurious correlations that lead models to correct predictions for the wrong reasons pose a critical challenge for robust real-world generalization. Existing research attributes this issue to group imbalance and addresses it by maximizing group-balanced or worst-group accuracy, which heavily relies on expensive bias annotations. A compromise approach involves predicting bias information using extensively pretrained foundation models, which requires large-scale data and becomes impractical for resource-limited rare domains. To address these challenges, we offer a novel perspective by reframing the spurious correlations as imbalances or mismatches in class-conditional distributions, and propose a simple yet effective robust learning method that eliminates the need for both bias annotations and predictions. With the goal of reducing the mutual information between spurious factors and label information, our method leverages a sample reweighting strategy to achieve class-conditional distribution balancing, which automatically highlights minority groups and classes, effectively dismantling spurious correlations and producing a debiased data distribution for classification. Extensive experiments and analysis demonstrate that our approach consistently delivers state-of-the-art performance, rivaling methods that rely on bias supervision.

Big Learning: A Universal Machine Learning Paradigm?

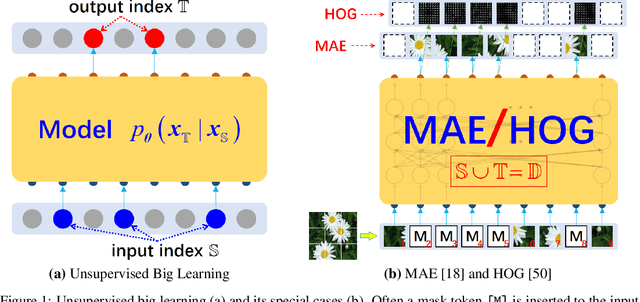
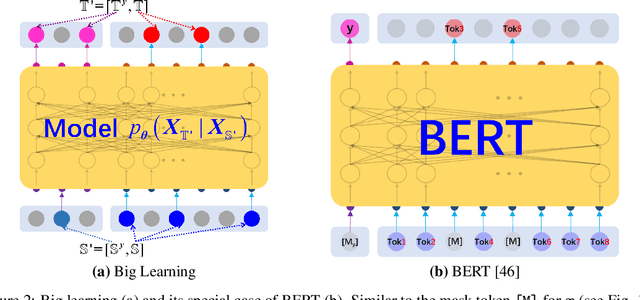
Recent breakthroughs based on big/foundation models reveal a vague avenue for artificial intelligence, that is, bid data, big/foundation models, big learning, $\cdots$. Following that avenue, here we elaborate on the newly introduced big learning. Specifically, big learning comprehensively exploits the available information inherent in large-scale complete/incomplete data, by simultaneously learning to model many-to-all joint/conditional/marginal data distributions (thus named big learning) with one universal foundation model. We reveal that big learning is what existing foundation models are implicitly doing; accordingly, our big learning provides high-level guidance for flexible design and improvements of foundation models, accelerating the true self-learning on the Internet. Besides, big learning ($i$) is equipped with marvelous flexibility for both training data and training-task customization; ($ii$) potentially delivers all joint/conditional/marginal data capabilities after training; ($iii$) significantly reduces the training-test gap with improved model generalization; and ($iv$) unifies conventional machine learning paradigms e.g. supervised learning, unsupervised learning, generative learning, etc. and enables their flexible cooperation, manifesting a universal learning paradigm.

Bridging Maximum Likelihood and Adversarial Learning via $α$-Divergence

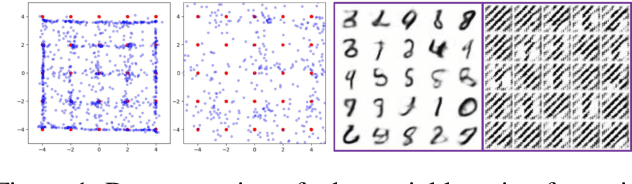
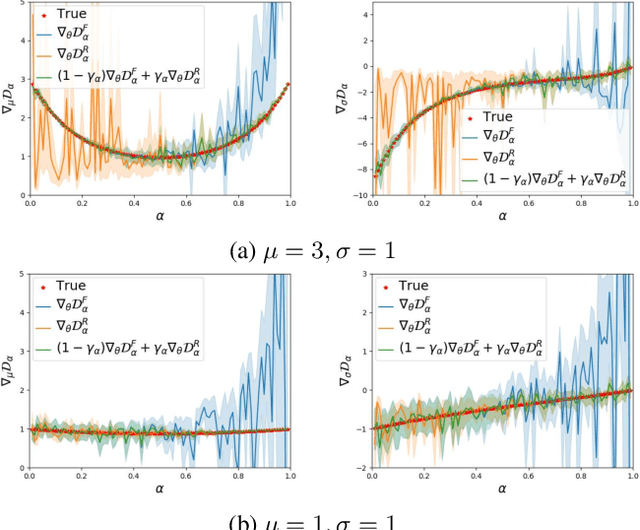
Maximum likelihood (ML) and adversarial learning are two popular approaches for training generative models, and from many perspectives these techniques are complementary. ML learning encourages the capture of all data modes, and it is typically characterized by stable training. However, ML learning tends to distribute probability mass diffusely over the data space, $e.g.$, yielding blurry synthetic images. Adversarial learning is well known to synthesize highly realistic natural images, despite practical challenges like mode dropping and delicate training. We propose an $\alpha$-Bridge to unify the advantages of ML and adversarial learning, enabling the smooth transfer from one to the other via the $\alpha$-divergence. We reveal that generalizations of the $\alpha$-Bridge are closely related to approaches developed recently to regularize adversarial learning, providing insights into that prior work, and further understanding of why the $\alpha$-Bridge performs well in practice.

GO Hessian for Expectation-Based Objectives

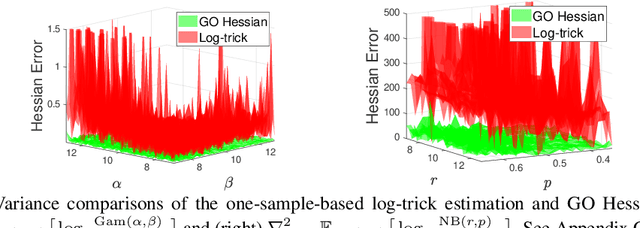
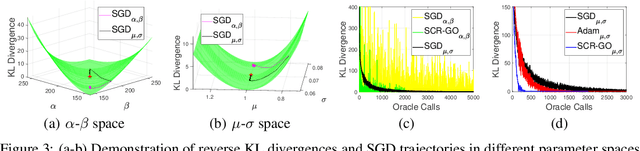
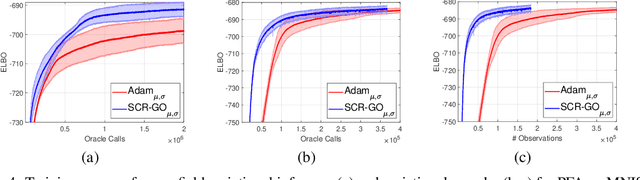
An unbiased low-variance gradient estimator, termed GO gradient, was proposed recently for expectation-based objectives $\mathbb{E}_{q_{\boldsymbol{\gamma}}(\boldsymbol{y})} [f(\boldsymbol{y})]$, where the random variable (RV) $\boldsymbol{y}$ may be drawn from a stochastic computation graph with continuous (non-reparameterizable) internal nodes and continuous/discrete leaves. Upgrading the GO gradient, we present for $\mathbb{E}_{q_{\boldsymbol{\boldsymbol{\gamma}}}(\boldsymbol{y})} [f(\boldsymbol{y})]$ an unbiased low-variance Hessian estimator, named GO Hessian. Considering practical implementation, we reveal that GO Hessian is easy-to-use with auto-differentiation and Hessian-vector products, enabling efficient cheap exploitation of curvature information over stochastic computation graphs. As representative examples, we present the GO Hessian for non-reparameterizable gamma and negative binomial RVs/nodes. Based on the GO Hessian, we design a new second-order method for $\mathbb{E}_{q_{\boldsymbol{\boldsymbol{\gamma}}}(\boldsymbol{y})} [f(\boldsymbol{y})]$, with rigorous experiments conducted to verify its effectiveness and efficiency.

GAN Memory with No Forgetting

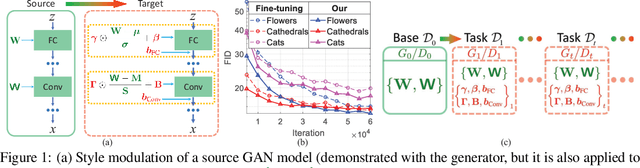
Seeking to address the fundamental issue of memory in lifelong learning, we propose a GAN memory that is capable of realistically remembering a stream of generative processes with \emph{no} forgetting. Our GAN memory is based on recognizing that one can modulate the ``style'' of a GAN model to form perceptually-distant targeted generation. Accordingly, we propose to do sequential style modulations atop a well-behaved base GAN model, to form sequential targeted generative models, while simultaneously benefiting from the transferred base knowledge. Experiments demonstrate the superiority of our method over existing approaches and its effectiveness in alleviating catastrophic forgetting for lifelong classification problems.

On Leveraging Pretrained GANs for Limited-Data Generation

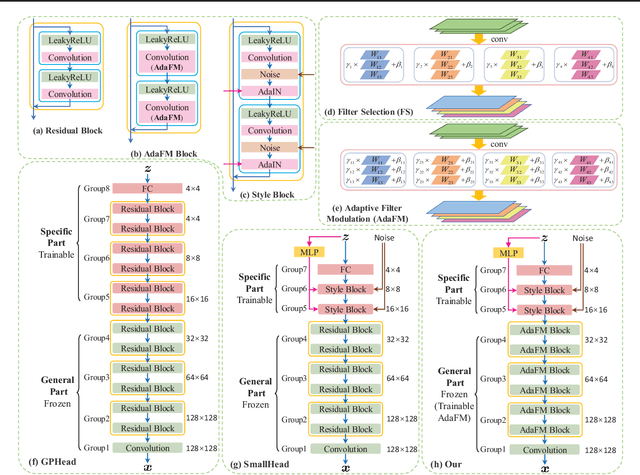
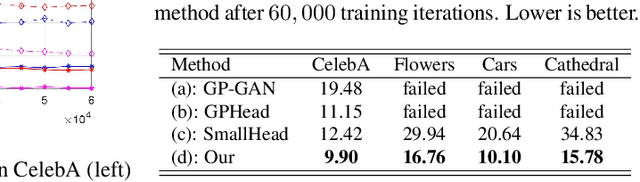
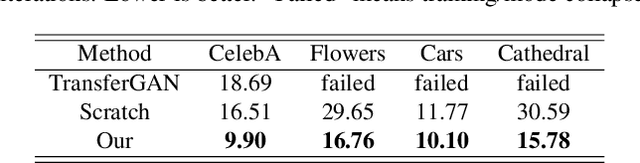
Recent work has shown GANs can generate highly realistic images that are indistinguishable by human. Of particular interest here is the empirical observation that most generated images are not contained in training datasets, indicating potential generalization with GANs. That generalizability makes it appealing to exploit GANs to help applications with limited available data, e.g., augment training data to alleviate overfitting. To better facilitate training a GAN on limited data, we propose to leverage already-available GAN models pretrained on large-scale datasets (like ImageNet) to introduce additional common knowledge (which may not exist within the limited data) following the transfer learning idea. Specifically, exampled by natural image generation tasks, we reveal the fact that low-level filters (those close to observations) of both the generator and discriminator of pretrained GANs can be transferred to help the target limited-data generation. For better adaption of the transferred filters to the target domain, we introduce a new technique named adaptive filter modulation (AdaFM), which provides boosted performance over baseline methods. Unifying the transferred filters and the introduced techniques, we present our method and conduct extensive experiments to demonstrate its training efficiency and better performance on limited-data generation.

GO Gradient for Expectation-Based Objectives

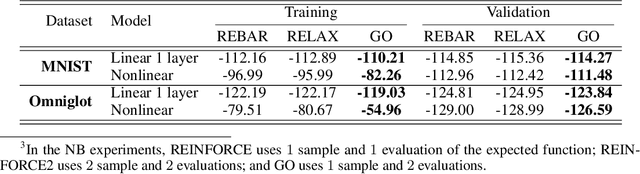
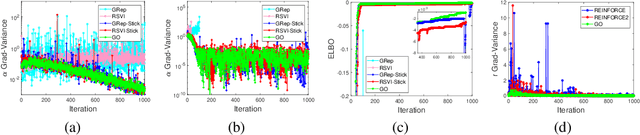
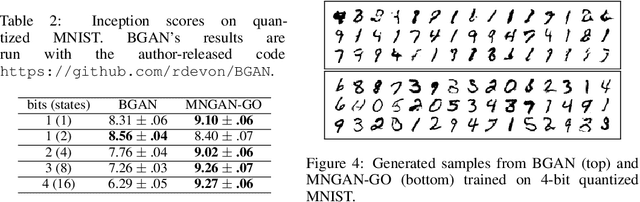
Within many machine learning algorithms, a fundamental problem concerns efficient calculation of an unbiased gradient wrt parameters $\gammav$ for expectation-based objectives $\Ebb_{q_{\gammav} (\yv)} [f(\yv)]$. Most existing methods either (i) suffer from high variance, seeking help from (often) complicated variance-reduction techniques; or (ii) they only apply to reparameterizable continuous random variables and employ a reparameterization trick. To address these limitations, we propose a General and One-sample (GO) gradient that (i) applies to many distributions associated with non-reparameterizable continuous or discrete random variables, and (ii) has the same low-variance as the reparameterization trick. We find that the GO gradient often works well in practice based on only one Monte Carlo sample (although one can of course use more samples if desired). Alongside the GO gradient, we develop a means of propagating the chain rule through distributions, yielding statistical back-propagation, coupling neural networks to common random variables.