Flow Matching for Generative Modeling

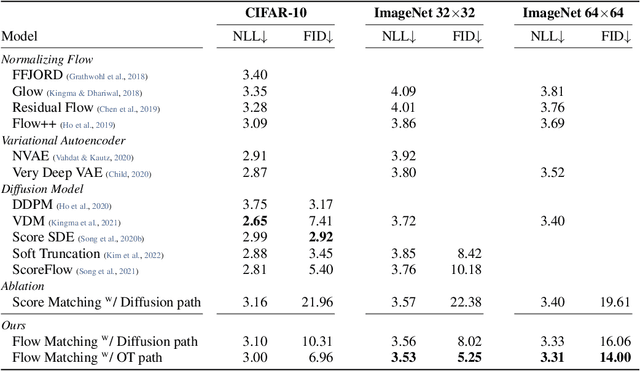
We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs based on regressing vector fields of fixed conditional probability paths. Flow Matching is compatible with a general family of Gaussian probability paths for transforming between noise and data samples -- which subsumes existing diffusion paths as specific instances. Interestingly, we find that employing FM with diffusion paths results in a more robust and stable alternative for training diffusion models. Furthermore, Flow Matching opens the door to training CNFs with other, non-diffusion probability paths. An instance of particular interest is using Optimal Transport (OT) displacement interpolation to define the conditional probability paths. These paths are more efficient than diffusion paths, provide faster training and sampling, and result in better generalization. Training CNFs using Flow Matching on ImageNet leads to state-of-the-art performance in terms of both likelihood and sample quality, and allows fast and reliable sample generation using off-the-shelf numerical ODE solvers.

Matching Normalizing Flows and Probability Paths on Manifolds

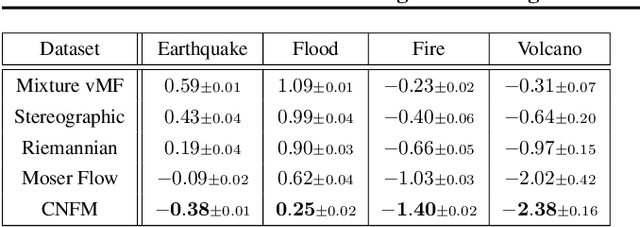
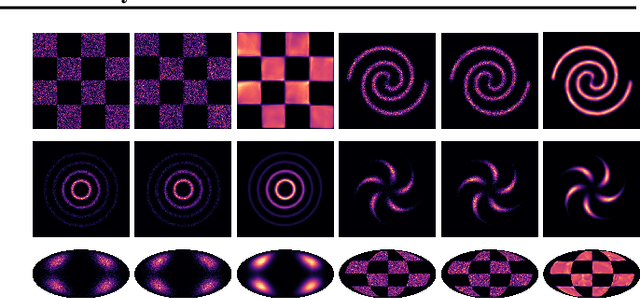
Continuous Normalizing Flows (CNFs) are a class of generative models that transform a prior distribution to a model distribution by solving an ordinary differential equation (ODE). We propose to train CNFs on manifolds by minimizing probability path divergence (PPD), a novel family of divergences between the probability density path generated by the CNF and a target probability density path. PPD is formulated using a logarithmic mass conservation formula which is a linear first order partial differential equation relating the log target probabilities and the CNF's defining vector field. PPD has several key benefits over existing methods: it sidesteps the need to solve an ODE per iteration, readily applies to manifold data, scales to high dimensions, and is compatible with a large family of target paths interpolating pure noise and data in finite time. Theoretically, PPD is shown to bound classical probability divergences. Empirically, we show that CNFs learned by minimizing PPD achieve state-of-the-art results in likelihoods and sample quality on existing low-dimensional manifold benchmarks, and is the first example of a generative model to scale to moderately high dimensional manifolds.

Semi-Discrete Normalizing Flows through Differentiable Tessellation

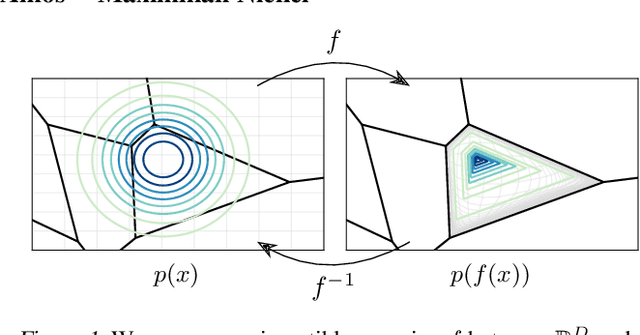
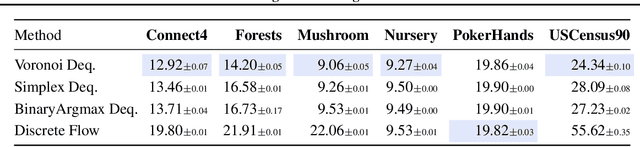
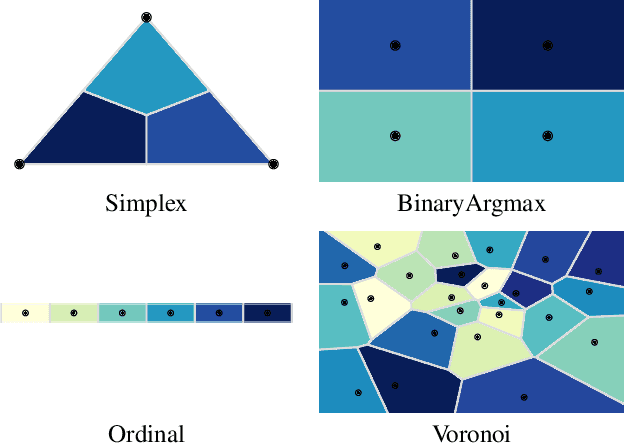
Mapping between discrete and continuous distributions is a difficult task and many have had to resort to approximate or heuristical approaches. We propose a tessellation-based approach that directly learns quantization boundaries on a continuous space, complete with exact likelihood evaluations. This is done through constructing normalizing flows on convex polytopes parameterized through a differentiable Voronoi tessellation. Using a simple homeomorphism with an efficient log determinant Jacobian, we can then cheaply parameterize distributions on convex polytopes. We explore this approach in two application settings, mapping from discrete to continuous and vice versa. Firstly, a Voronoi dequantization allows automatically learning quantization boundaries in a multidimensional space. The location of boundaries and distances between regions can encode useful structural relations between the quantized discrete values. Secondly, a Voronoi mixture model has constant computation cost for likelihood evaluation regardless of the number of mixture components. Empirically, we show improvements over existing methods across a range of structured data modalities, and find that we can achieve a significant gain from just adding Voronoi mixtures to a baseline model.

Can I see an Example? Active Learning the Long Tail of Attributes and Relations

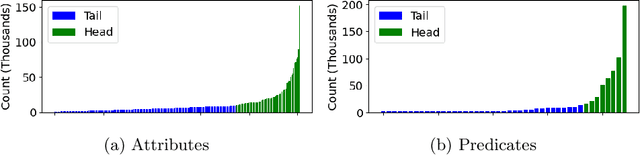
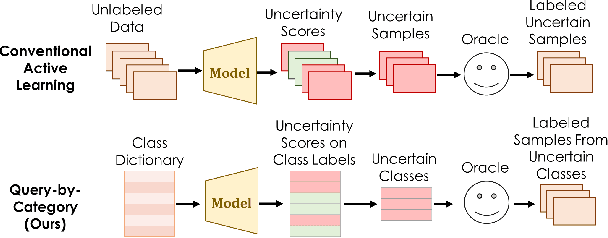
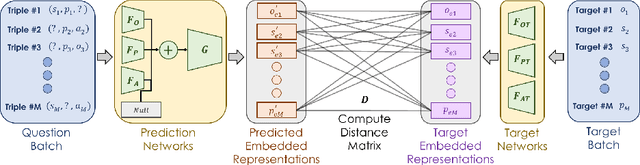
There has been significant progress in creating machine learning models that identify objects in scenes along with their associated attributes and relationships; however, there is a large gap between the best models and human capabilities. One of the major reasons for this gap is the difficulty in collecting sufficient amounts of annotated relations and attributes for training these systems. While some attributes and relations are abundant, the distribution in the natural world and existing datasets is long tailed. In this paper, we address this problem by introducing a novel incremental active learning framework that asks for attributes and relations in visual scenes. While conventional active learning methods ask for labels of specific examples, we flip this framing to allow agents to ask for examples from specific categories. Using this framing, we introduce an active sampling method that asks for examples from the tail of the data distribution and show that it outperforms classical active learning methods on Visual Genome.

Moser Flow: Divergence-based Generative Modeling on Manifolds

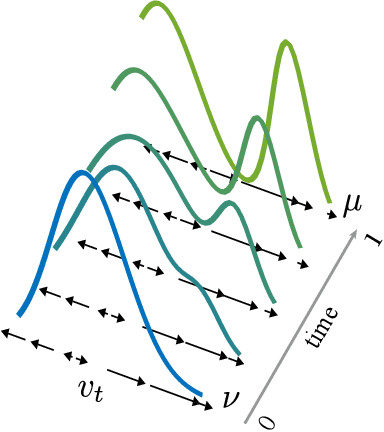
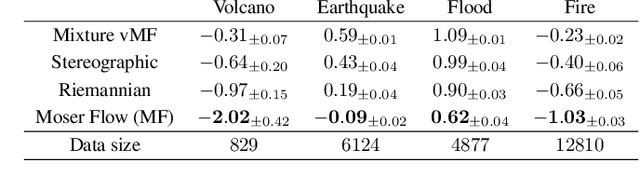
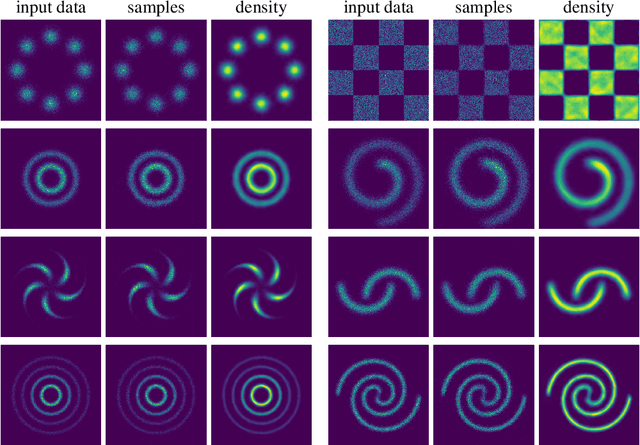
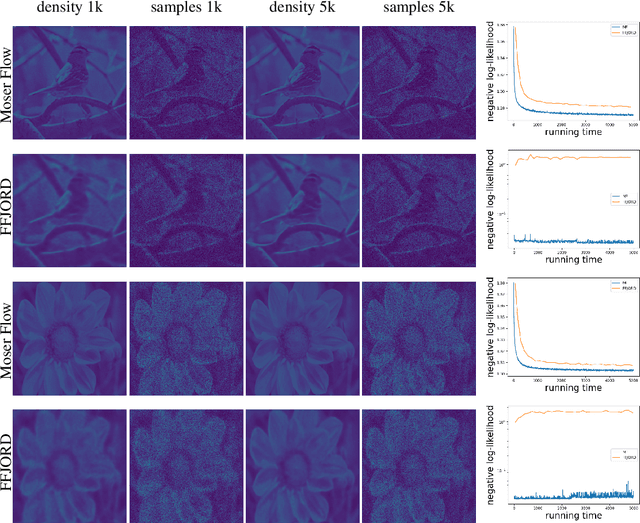
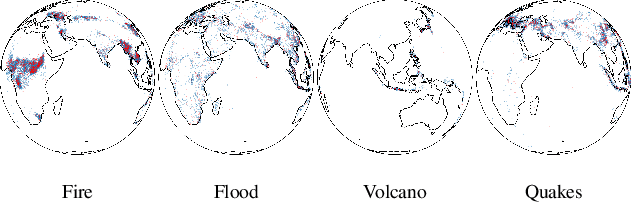
We are interested in learning generative models for complex geometries described via manifolds, such as spheres, tori, and other implicit surfaces. Current extensions of existing (Euclidean) generative models are restricted to specific geometries and typically suffer from high computational costs. We introduce Moser Flow (MF), a new class of generative models within the family of continuous normalizing flows (CNF). MF also produces a CNF via a solution to the change-of-variable formula, however differently from other CNF methods, its model (learned) density is parameterized as the source (prior) density minus the divergence of a neural network (NN). The divergence is a local, linear differential operator, easy to approximate and calculate on manifolds. Therefore, unlike other CNFs, MF does not require invoking or backpropagating through an ODE solver during training. Furthermore, representing the model density explicitly as the divergence of a NN rather than as a solution of an ODE facilitates learning high fidelity densities. Theoretically, we prove that MF constitutes a universal density approximator under suitable assumptions. Empirically, we demonstrate for the first time the use of flow models for sampling from general curved surfaces and achieve significant improvements in density estimation, sample quality, and training complexity over existing CNFs on challenging synthetic geometries and real-world benchmarks from the earth and climate sciences.

Neural Spatio-Temporal Point Processes

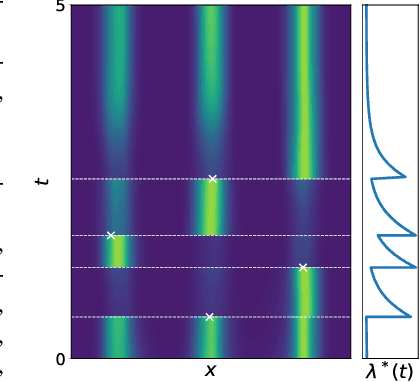
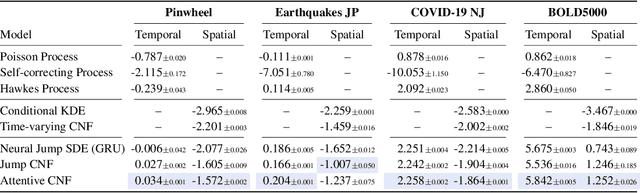
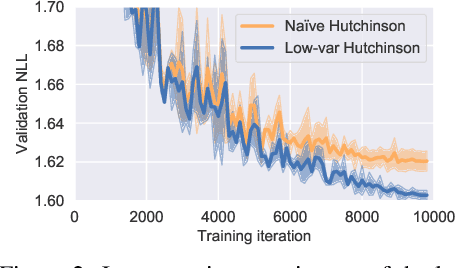
We propose a new class of parameterizations for spatio-temporal point processes which leverage Neural ODEs as a computational method and enable flexible, high-fidelity models of discrete events that are localized in continuous time and space. Central to our approach is a combination of recurrent continuous-time neural networks with two novel neural architectures, i.e., Jump and Attentive Continuous-time Normalizing Flows. This approach allows us to learn complex distributions for both the spatial and temporal domain and to condition non-trivially on the observed event history. We validate our models on data sets from a wide variety of contexts such as seismology, epidemiology, urban mobility, and neuroscience.

Learning Neural Event Functions for Ordinary Differential Equations

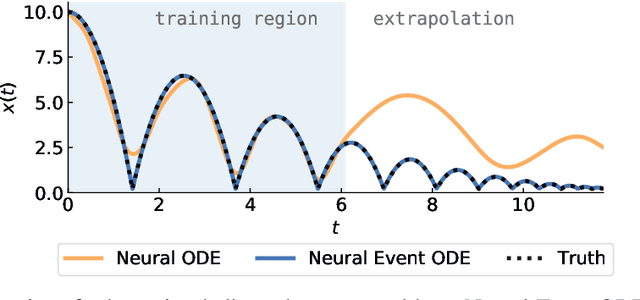
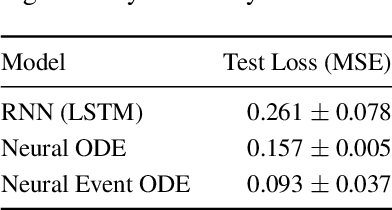
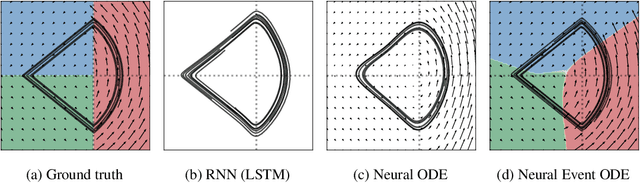
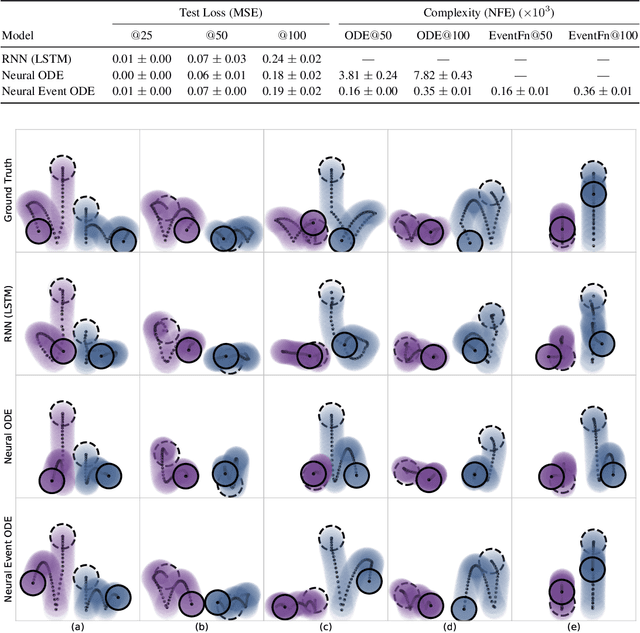
The existing Neural ODE formulation relies on an explicit knowledge of the termination time. We extend Neural ODEs to implicitly defined termination criteria modeled by neural event functions, which can be chained together and differentiated through. Neural Event ODEs are capable of modeling discrete (instantaneous) changes in a continuous-time system, without prior knowledge of when these changes should occur or how many such changes should exist. We test our approach in modeling hybrid discrete- and continuous- systems such as switching dynamical systems and collision in multi-body systems, and we propose simulation-based training of point processes with applications in discrete control.

CURI: A Benchmark for Productive Concept Learning Under Uncertainty

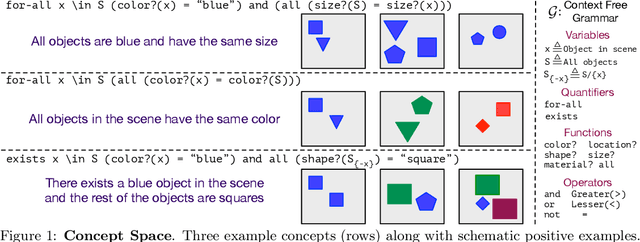
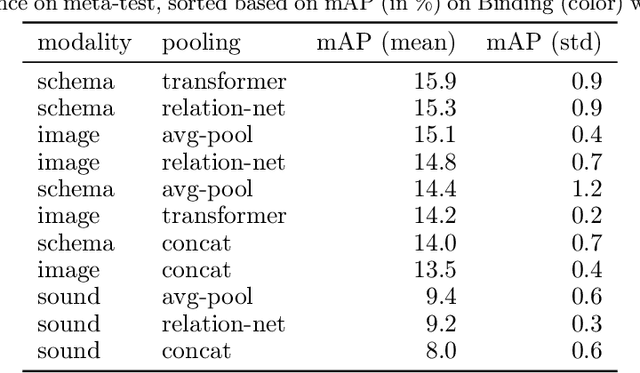
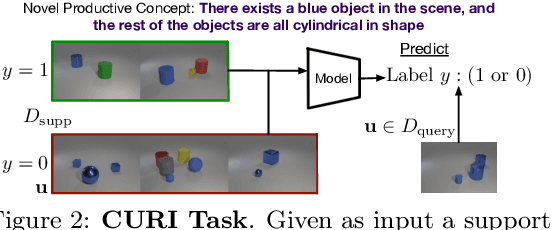
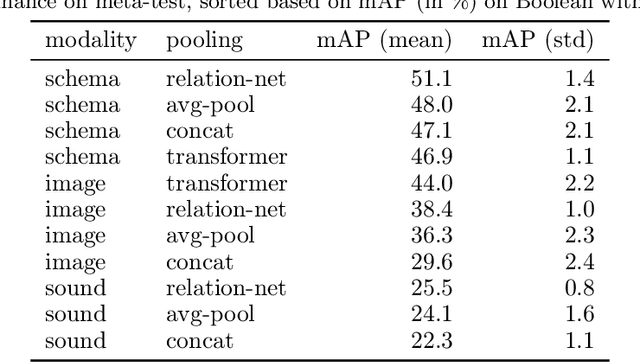
Humans can learn and reason under substantial uncertainty in a space of infinitely many concepts, including structured relational concepts ("a scene with objects that have the same color") and ad-hoc categories defined through goals ("objects that could fall on one's head"). In contrast, standard classification benchmarks: 1) consider only a fixed set of category labels, 2) do not evaluate compositional concept learning and 3) do not explicitly capture a notion of reasoning under uncertainty. We introduce a new few-shot, meta-learning benchmark, Compositional Reasoning Under Uncertainty (CURI) to bridge this gap. CURI evaluates different aspects of productive and systematic generalization, including abstract understandings of disentangling, productive generalization, learning boolean operations, variable binding, etc. Importantly, it also defines a model-independent "compositionality gap" to evaluate the difficulty of generalizing out-of-distribution along each of these axes. Extensive evaluations across a range of modeling choices spanning different modalities (image, schemas, and sounds), splits, privileged auxiliary concept information, and choices of negatives reveal substantial scope for modeling advances on the proposed task. All code and datasets will be available online.

Riemannian Continuous Normalizing Flows

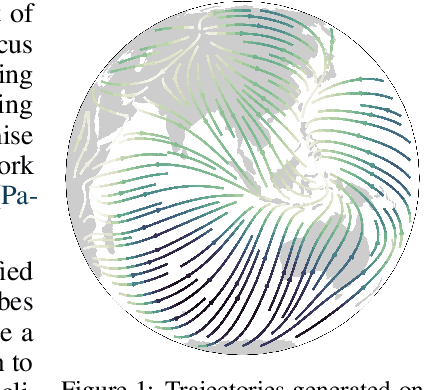
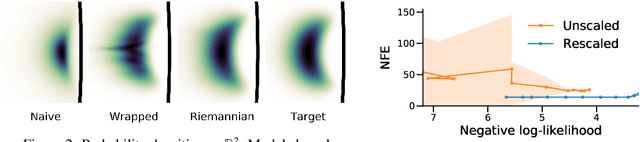
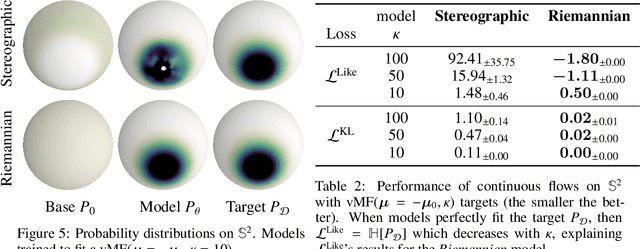
Normalizing flows have shown great promise for modelling flexible probability distributions in a computationally tractable way. However, whilst data is often naturally described on Riemannian manifolds such as spheres, torii, and hyperbolic spaces, most normalizing flows implicitly assume a flat geometry, making them either misspecified or ill-suited in these situations. To overcome this problem, we introduce Riemannian continuous normalizing flows, a model which admits the parametrization of flexible probability measures on smooth manifolds by defining flows as the solution to ordinary differential equations. We show that this approach can lead to substantial improvements on both synthetic and real-world data when compared to standard flows or previously introduced projected flows.

Learning Multivariate Hawkes Processes at Scale

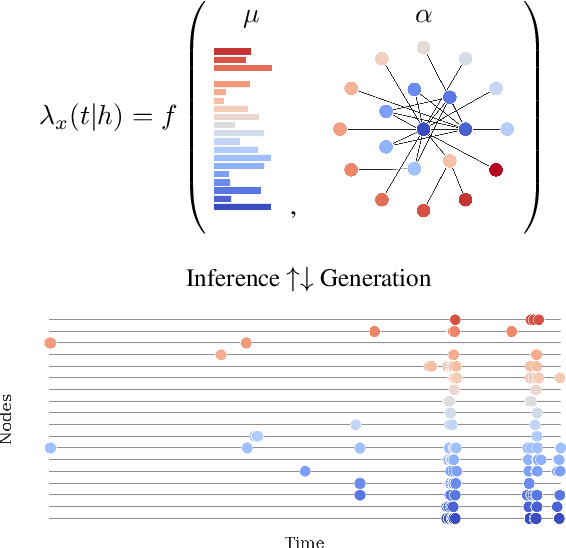
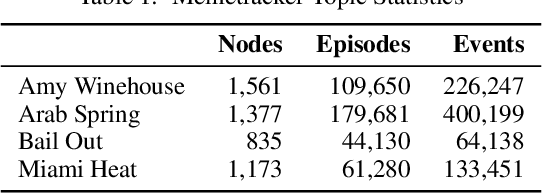
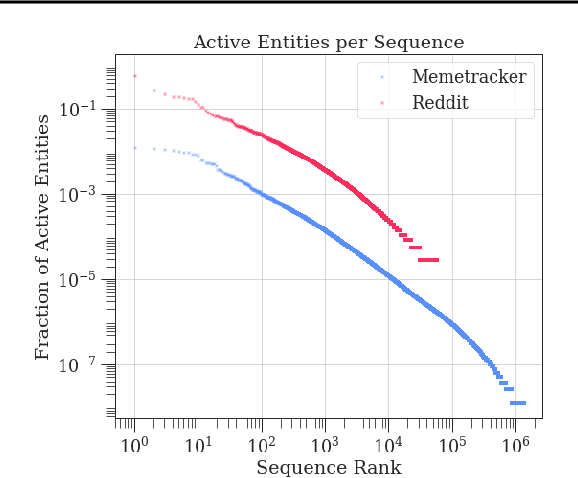
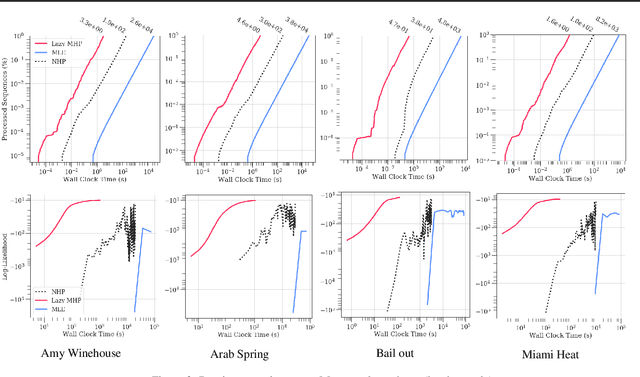
Multivariate Hawkes Processes (MHPs) are an important class of temporal point processes that have enabled key advances in understanding and predicting social information systems. However, due to their complex modeling of temporal dependencies, MHPs have proven to be notoriously difficult to scale, what has limited their applications to relatively small domains. In this work, we propose a novel model and computational approach to overcome this important limitation. By exploiting a characteristic sparsity pattern in real-world diffusion processes, we show that our approach allows to compute the exact likelihood and gradients of an MHP -- independently of the ambient dimensions of the underlying network. We show on synthetic and real-world datasets that our model does not only achieve state-of-the-art predictive results, but also improves runtime performance by multiple orders of magnitude compared to standard methods on sparse event sequences. In combination with easily interpretable latent variables and influence structures, this allows us to analyze diffusion processes at previously unattainable scale.