Max Welling
UC Irvine
The Hintons in your Neural Network: a Quantum Field Theory View of Deep Learning
Mar 08, 2021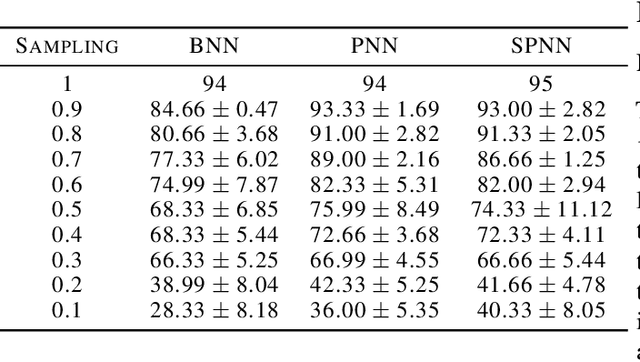
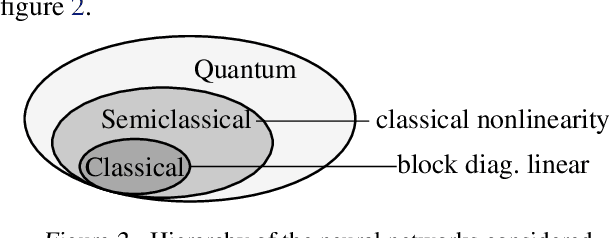
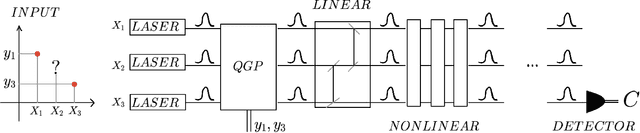
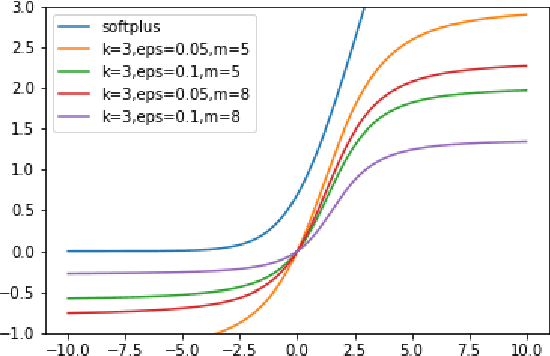
Abstract:In this work we develop a quantum field theory formalism for deep learning, where input signals are encoded in Gaussian states, a generalization of Gaussian processes which encode the agent's uncertainty about the input signal. We show how to represent linear and non-linear layers as unitary quantum gates, and interpret the fundamental excitations of the quantum model as particles, dubbed ``Hintons''. On top of opening a new perspective and techniques for studying neural networks, the quantum formulation is well suited for optical quantum computing, and provides quantum deformations of neural networks that can be run efficiently on those devices. Finally, we discuss a semi-classical limit of the quantum deformed models which is amenable to classical simulation.
Efficient Causal Inference from Combined Observational and Interventional Data through Causal Reductions
Mar 08, 2021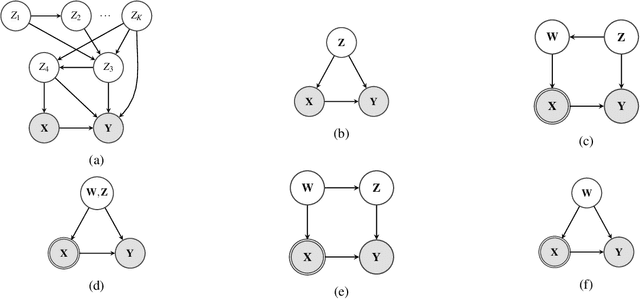

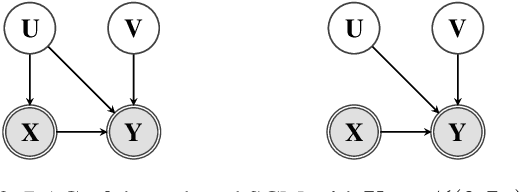
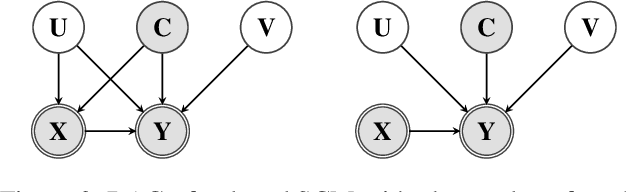
Abstract:Unobserved confounding is one of the main challenges when estimating causal effects. We propose a novel causal reduction method that replaces an arbitrary number of possibly high-dimensional latent confounders with a single latent confounder that lives in the same space as the treatment variable without changing the observational and interventional distributions entailed by the causal model. After the reduction, we parameterize the reduced causal model using a flexible class of transformations, so-called normalizing flows. We propose a learning algorithm to estimate the parameterized reduced model jointly from observational and interventional data. This allows us to estimate the causal effect in a principled way from combined data. We perform a series of experiments on data simulated using nonlinear causal mechanisms and find that we can often substantially reduce the number of interventional samples when adding observational training samples without sacrificing accuracy. Thus, adding observational data may help to more accurately estimate causal effects even in the presence of unobserved confounders.
Sampling in Combinatorial Spaces with SurVAE Flow Augmented MCMC
Mar 01, 2021
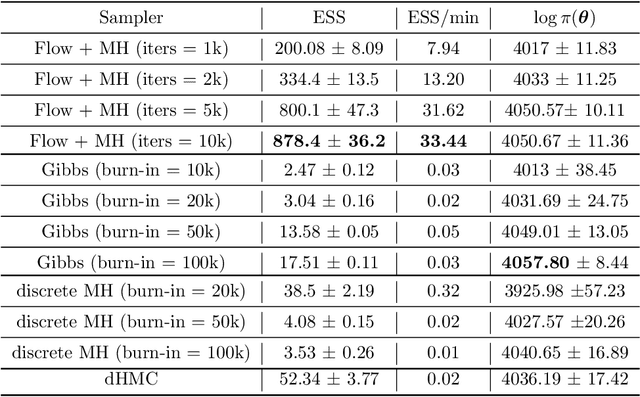

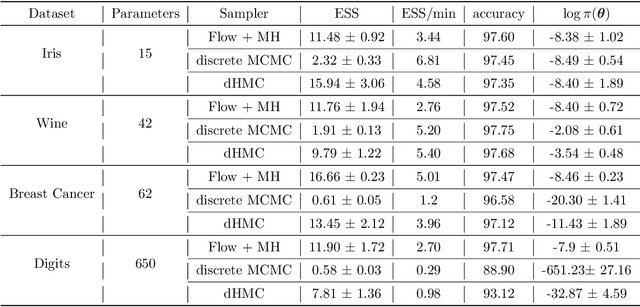
Abstract:Hybrid Monte Carlo is a powerful Markov Chain Monte Carlo method for sampling from complex continuous distributions. However, a major limitation of HMC is its inability to be applied to discrete domains due to the lack of gradient signal. In this work, we introduce a new approach based on augmenting Monte Carlo methods with SurVAE Flows to sample from discrete distributions using a combination of neural transport methods like normalizing flows and variational dequantization, and the Metropolis-Hastings rule. Our method first learns a continuous embedding of the discrete space using a surjective map and subsequently learns a bijective transformation from the continuous space to an approximately Gaussian distributed latent variable. Sampling proceeds by simulating MCMC chains in the latent space and mapping these samples to the target discrete space via the learned transformations. We demonstrate the efficacy of our algorithm on a range of examples from statistics, computational physics and machine learning, and observe improvements compared to alternative algorithms.
Batch Bayesian Optimization on Permutations using Acquisition Weighted Kernels
Feb 26, 2021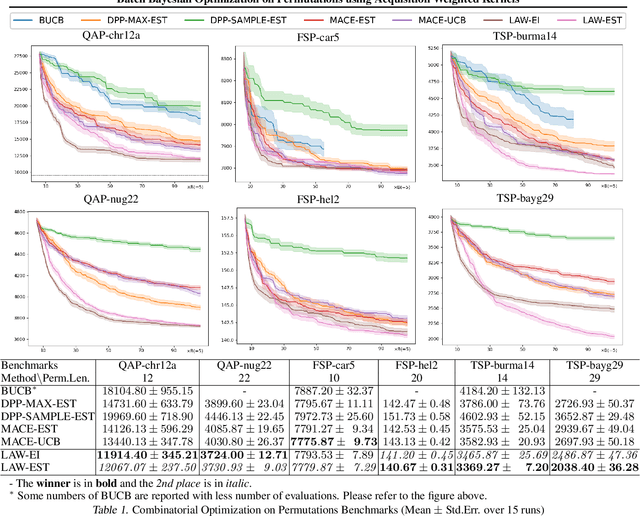

Abstract:In this work we propose a batch Bayesian optimization method for combinatorial problems on permutations, which is well suited for expensive cost functions on permutations. We introduce LAW, a new efficient batch acquisition method based on the determinantal point process, using an acquisition weighted kernel. Relying on multiple parallel evaluations, LAW accelerates the search for the optimal permutation. We provide a regret analysis for our method to gain insight in its theoretical properties. We then apply the framework to permutation problems, which have so far received little attention in the Bayesian Optimization literature, despite their practical importance. We call this method LAW2ORDER. We evaluate the method on several standard combinatorial problems involving permutations such as quadratic assignment, flowshop scheduling and the traveling salesman, as well as on a structure learning task.
Mixed Variable Bayesian Optimization with Frequency Modulated Kernels
Feb 25, 2021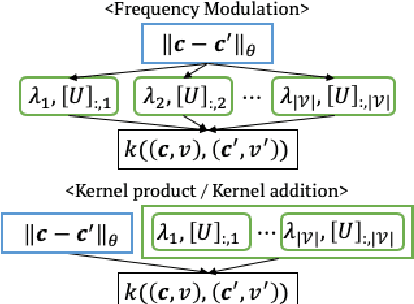
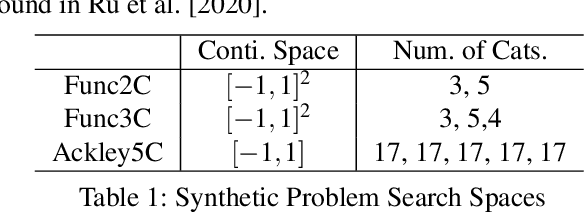
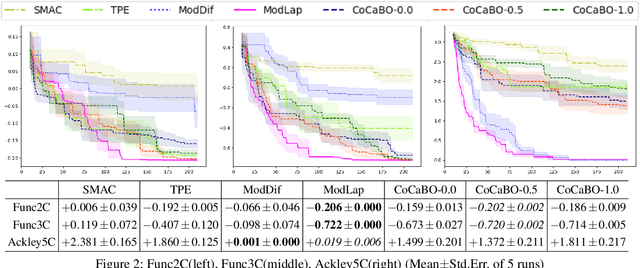

Abstract:The sample efficiency of Bayesian optimization(BO) is often boosted by Gaussian Process(GP) surrogate models. However, on mixed variable spaces, surrogate models other than GPs are prevalent, mainly due to the lack of kernels which can model complex dependencies across different types of variables. In this paper, we propose the frequency modulated (FM) kernel flexibly modeling dependencies among different types of variables, so that BO can enjoy the further improved sample efficiency. The FM kernel uses distances on continuous variables to modulate the graph Fourier spectrum derived from discrete variables. However, the frequency modulation does not always define a kernel with the similarity measure behavior which returns higher values for pairs of more similar points. Therefore, we specify and prove conditions for FM kernels to be positive definite and to exhibit the similarity measure behavior. In experiments, we demonstrate the improved sample efficiency of GP BO using FM kernels (BO-FM).On synthetic problems and hyperparameter optimization problems, BO-FM outperforms competitors consistently. Also, the importance of the frequency modulation principle is empirically demonstrated on the same problems. On joint optimization of neural architectures and SGD hyperparameters, BO-FM outperforms competitors including Regularized evolution(RE) and BOHB. Remarkably, BO-FM performs better even than RE and BOHB using three times as many evaluations.
Deep Policy Dynamic Programming for Vehicle Routing Problems
Feb 23, 2021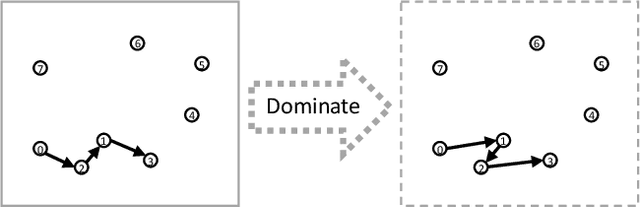
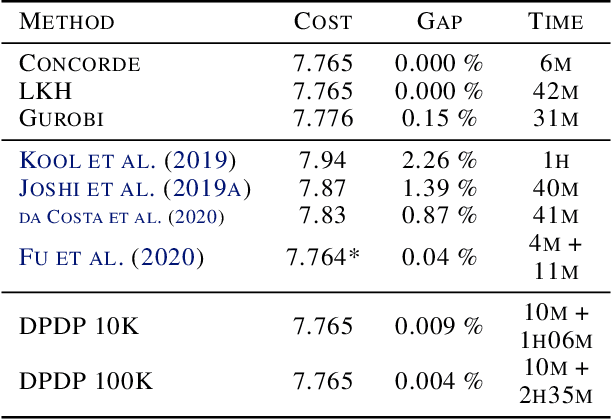
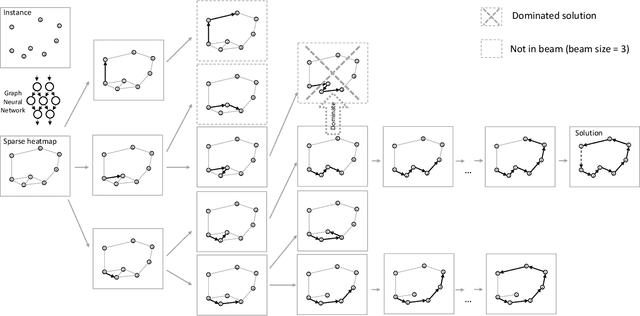
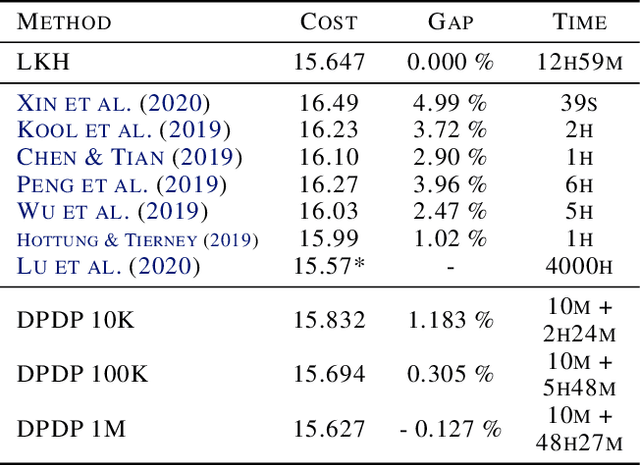
Abstract:Routing problems are a class of combinatorial problems with many practical applications. Recently, end-to-end deep learning methods have been proposed to learn approximate solution heuristics for such problems. In contrast, classical dynamic programming (DP) algorithms can find optimal solutions, but scale badly with the problem size. We propose Deep Policy Dynamic Programming (DPDP), which aims to combine the strengths of learned neural heuristics with those of DP algorithms. DPDP prioritizes and restricts the DP state space using a policy derived from a deep neural network, which is trained to predict edges from example solutions. We evaluate our framework on the travelling salesman problem (TSP) and the vehicle routing problem (VRP) and show that the neural policy improves the performance of (restricted) DP algorithms, making them competitive to strong alternatives such as LKH, while also outperforming other `neural approaches' for solving TSPs and VRPs with 100 nodes.
E(n) Equivariant Graph Neural Networks
Feb 19, 2021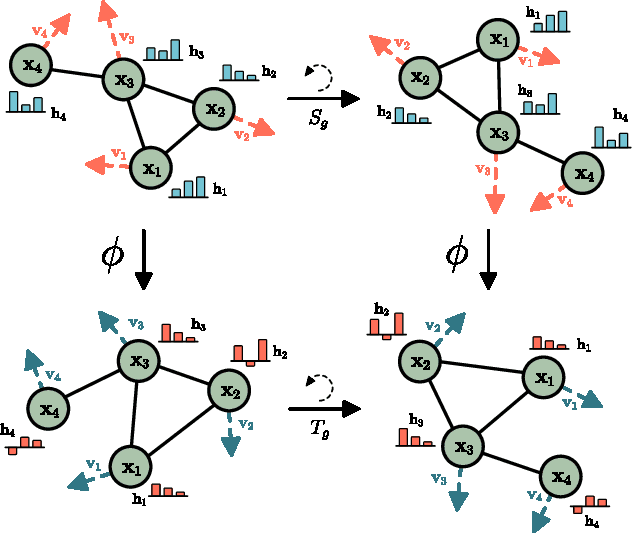

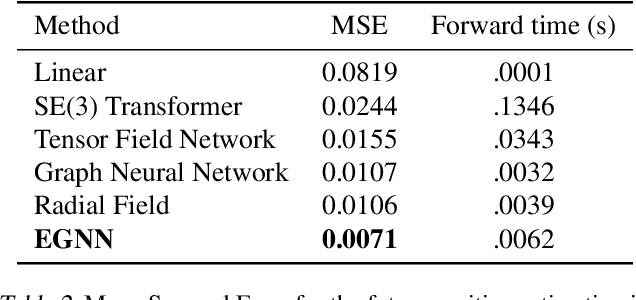
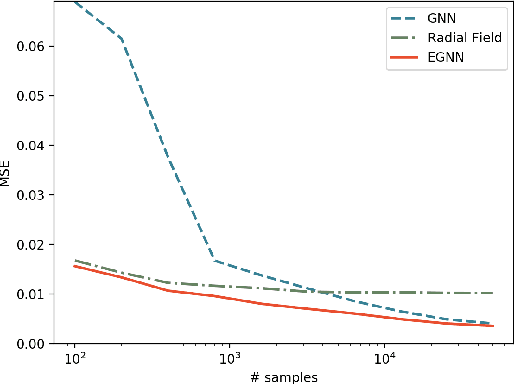
Abstract:This paper introduces a new model to learn graph neural networks equivariant to rotations, translations, reflections and permutations called E(n)-Equivariant Graph Neural Networks (EGNNs). In contrast with existing methods, our work does not require computationally expensive higher-order representations in intermediate layers while it still achieves competitive or better performance. In addition, whereas existing methods are limited to equivariance on 3 dimensional spaces, our model is easily scaled to higher-dimensional spaces. We demonstrate the effectiveness of our method on dynamical systems modelling, representation learning in graph autoencoders and predicting molecular properties.
Argmax Flows and Multinomial Diffusion: Towards Non-Autoregressive Language Models
Feb 10, 2021

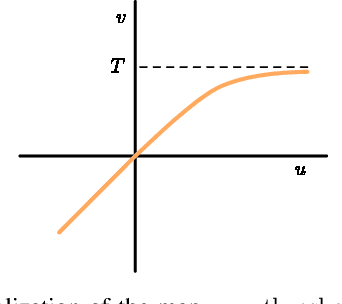

Abstract:The field of language modelling has been largely dominated by autoregressive models, for which sampling is inherently difficult to parallelize. This paper introduces two new classes of generative models for categorical data such as language or image segmentation: Argmax Flows and Multinomial Diffusion. Argmax Flows are defined by a composition of a continuous distribution (such as a normalizing flow), and an argmax function. To optimize this model, we learn a probabilistic inverse for the argmax that lifts the categorical data to a continuous space. Multinomial Diffusion gradually adds categorical noise in a diffusion process, for which the generative denoising process is learned. We demonstrate that our models perform competitively on language modelling and modelling of image segmentation maps.
Self Normalizing Flows
Nov 14, 2020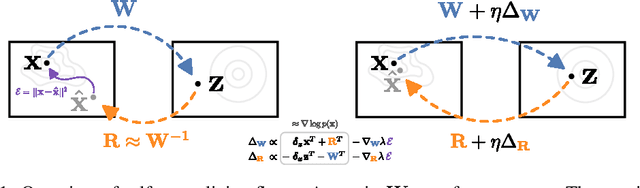
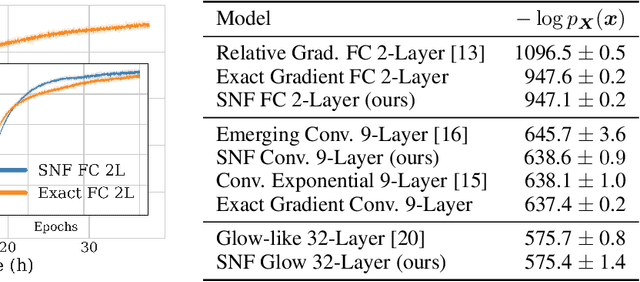
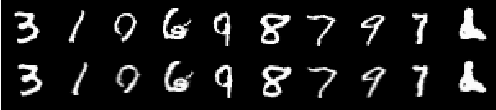

Abstract:Efficient gradient computation of the Jacobian determinant term is a core problem of the normalizing flow framework. Thus, most proposed flow models either restrict to a function class with easy evaluation of the Jacobian determinant, or an efficient estimator thereof. However, these restrictions limit the performance of such density models, frequently requiring significant depth to reach desired performance levels. In this work, we propose Self Normalizing Flows, a flexible framework for training normalizing flows by replacing expensive terms in the gradient by learned approximate inverses at each layer. This reduces the computational complexity of each layer's exact update from $\mathcal{O}(D^3)$ to $\mathcal{O}(D^2)$, allowing for the training of flow architectures which were otherwise computationally infeasible, while also providing efficient sampling. We show experimentally that such models are remarkably stable and optimize to similar data likelihood values as their exact gradient counterparts, while surpassing the performance of their functionally constrained counterparts.
Experimental design for MRI by greedy policy search
Oct 30, 2020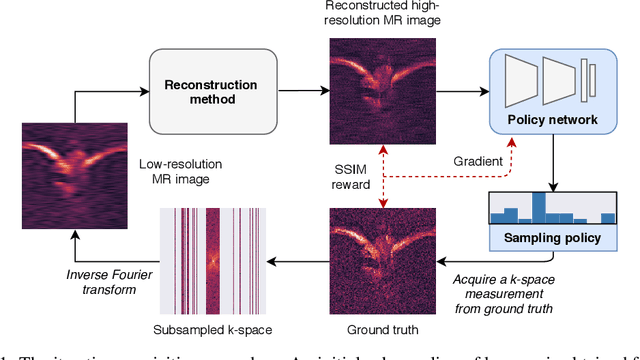
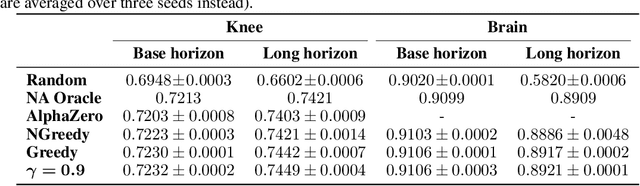
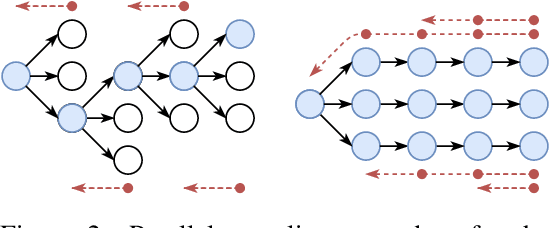
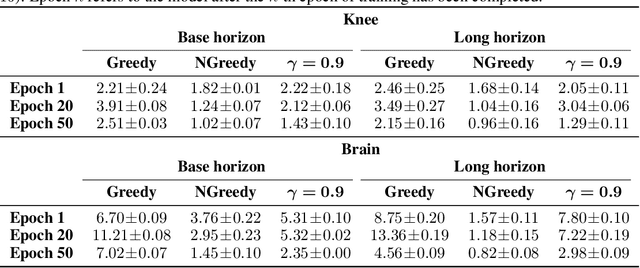
Abstract:In today's clinical practice, magnetic resonance imaging (MRI) is routinely accelerated through subsampling of the associated Fourier domain. Currently, the construction of these subsampling strategies - known as experimental design - relies primarily on heuristics. We propose to learn experimental design strategies for accelerated MRI with policy gradient methods. Unexpectedly, our experiments show that a simple greedy approximation of the objective leads to solutions nearly on-par with the more general non-greedy approach. We offer a partial explanation for this phenomenon rooted in greater variance in the non-greedy objective's gradient estimates, and experimentally verify that this variance hampers non-greedy models in adapting their policies to individual MR images. We empirically show that this adaptivity is key to improving subsampling designs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge