STARK denoises spatial transcriptomics images via adaptive regularization

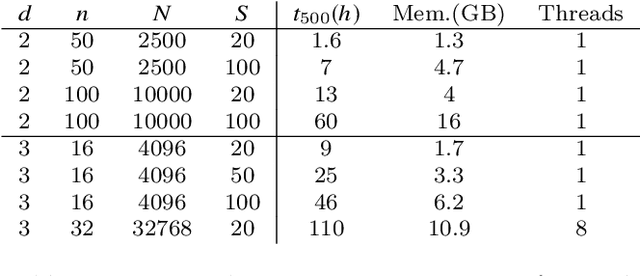
We present an approach to denoising spatial transcriptomics images that is particularly effective for uncovering cell identities in the regime of ultra-low sequencing depths, and also allows for interpolation of gene expression. The method -- Spatial Transcriptomics via Adaptive Regularization and Kernels (STARK) -- augments kernel ridge regression with an incrementally adaptive graph Laplacian regularizer. In each iteration, we (1) perform kernel ridge regression with a fixed graph to update the image, and (2) update the graph based on the new image. The kernel ridge regression step involves reducing the infinite dimensional problem on a space of images to finite dimensions via a modified representer theorem. Starting with a purely spatial graph, and updating it as we improve our image makes the graph more robust to noise in low sequencing depth regimes. We show that the aforementioned approach optimizes a block-convex objective through an alternating minimization scheme wherein the sub-problems have closed form expressions that are easily computed. This perspective allows us to prove convergence of the iterates to a stationary point of this non-convex objective. Statistically, such stationary points converge to the ground truth with rate $\mathcal{O}(R^{-1/2})$ where $R$ is the number of reads. In numerical experiments on real spatial transcriptomics data, the denoising performance of STARK, evaluated in terms of label transfer accuracy, shows consistent improvement over the competing methods tested.

Trajectory Inference via Mean-field Langevin in Path Space

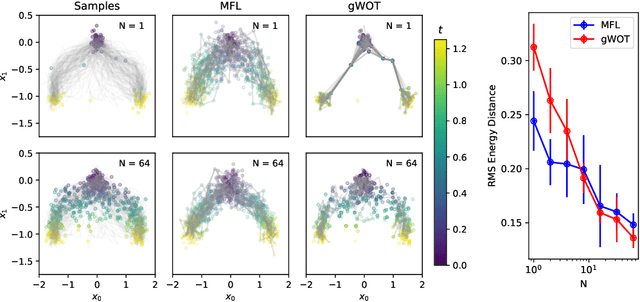
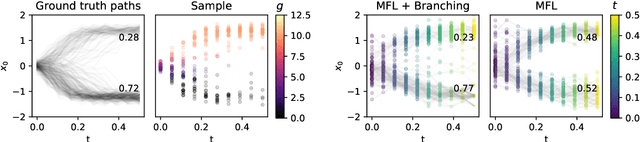
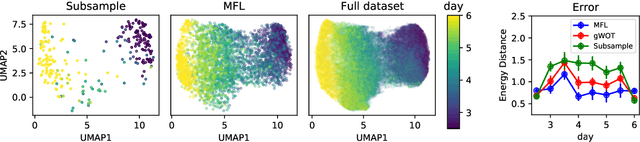
Trajectory inference aims at recovering the dynamics of a population from snapshots of its temporal marginals. To solve this task, a min-entropy estimator relative to the Wiener measure in path space was introduced by Lavenant et al. arXiv:2102.09204, and shown to consistently recover the dynamics of a large class of drift-diffusion processes from the solution of an infinite dimensional convex optimization problem. In this paper, we introduce a grid-free algorithm to compute this estimator. Our method consists in a family of point clouds (one per snapshot) coupled via Schr\"odinger bridges which evolve with noisy gradient descent. We study the mean-field limit of the dynamics and prove its global convergence at an exponential rate to the desired estimator. Overall, this leads to an inference method with end-to-end theoretical guarantees that solves an interpretable model for trajectory inference. We also present how to adapt the method to deal with mass variations, a useful extension when dealing with single cell RNA-sequencing data where cells can branch and die.

Ground Metric Learning on Graphs

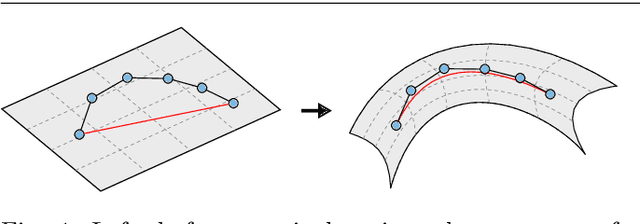
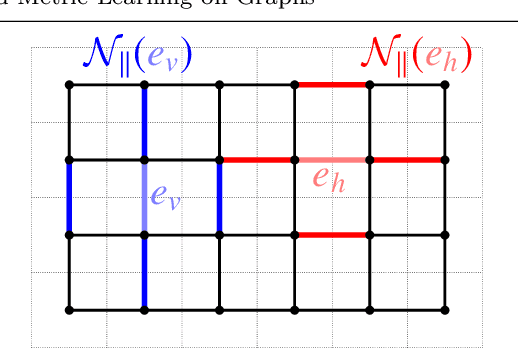
Optimal transport (OT) distances between probability distributions are parameterized by the ground metric they use between observations. Their relevance for real-life applications strongly hinges on whether that ground metric parameter is suitably chosen. Selecting it adaptively and algorithmically from prior knowledge, the so-called ground metric learning GML) problem, has therefore appeared in various settings. We consider it in this paper when the learned metric is constrained to be a geodesic distance on a graph that supports the measures of interest. This imposes a rich structure for candidate metrics, but also enables far more efficient learning procedures when compared to a direct optimization over the space of all metric matrices. We use this setting to tackle an inverse problem stemming from the observation of a density evolving with time: we seek a graph ground metric such that the OT interpolation between the starting and ending densities that result from that ground metric agrees with the observed evolution. This OT dynamic framework is relevant to model natural phenomena exhibiting displacements of mass, such as for instance the evolution of the color palette induced by the modification of lighting and materials.

Wasserstein Dictionary Learning: Optimal Transport-based unsupervised non-linear dictionary learning

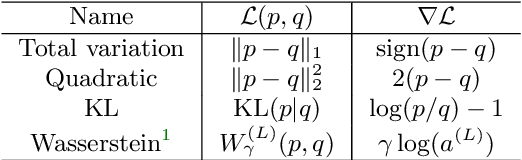
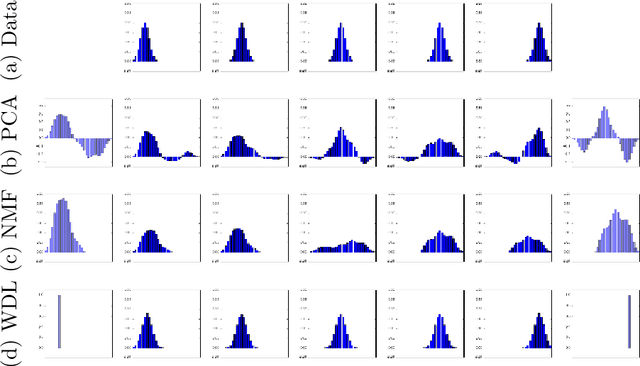
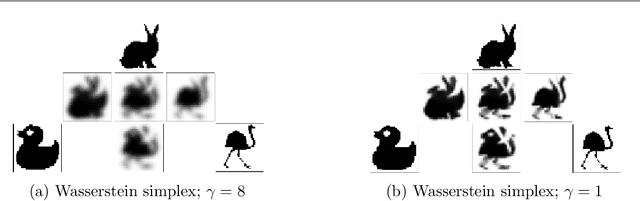
This paper introduces a new nonlinear dictionary learning method for histograms in the probability simplex. The method leverages optimal transport theory, in the sense that our aim is to reconstruct histograms using so-called displacement interpolations (a.k.a. Wasserstein barycenters) between dictionary atoms; such atoms are themselves synthetic histograms in the probability simplex. Our method simultaneously estimates such atoms, and, for each datapoint, the vector of weights that can optimally reconstruct it as an optimal transport barycenter of such atoms. Our method is computationally tractable thanks to the addition of an entropic regularization to the usual optimal transportation problem, leading to an approximation scheme that is efficient, parallel and simple to differentiate. Both atoms and weights are learned using a gradient-based descent method. Gradients are obtained by automatic differentiation of the generalized Sinkhorn iterations that yield barycenters with entropic smoothing. Because of its formulation relying on Wasserstein barycenters instead of the usual matrix product between dictionary and codes, our method allows for nonlinear relationships between atoms and the reconstruction of input data. We illustrate its application in several different image processing settings.