Regret Bounds for Kernel-Based Reinforcement Learning

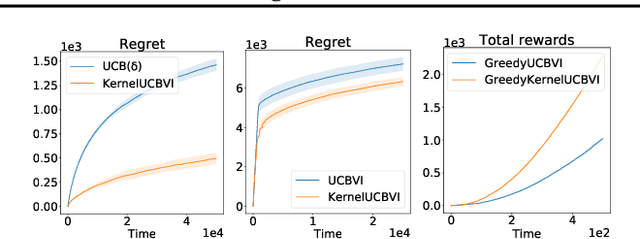
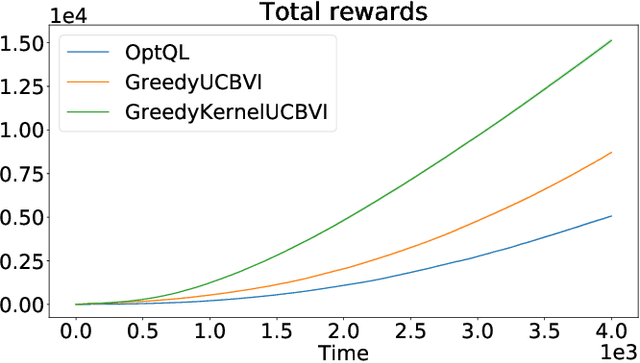
We consider the exploration-exploitation dilemma in finite-horizon reinforcement learning problems whose state-action space is endowed with a metric. We introduce Kernel-UCBVI, a model-based optimistic algorithm that leverages the smoothness of the MDP and a non-parametric kernel estimator of the rewards and transitions to efficiently balance exploration and exploitation. Unlike existing approaches with regret guarantees, it does not use any kind of partitioning of the state-action space. For problems with $K$ episodes and horizon $H$, we provide a regret bound of $O\left( H^3 K^{\max\left(\frac{1}{2}, \frac{2d}{2d+1}\right)}\right)$, where $d$ is the covering dimension of the joint state-action space. We empirically validate Kernel-UCBVI on discrete and continuous MDPs.

Active Model Estimation in Markov Decision Processes

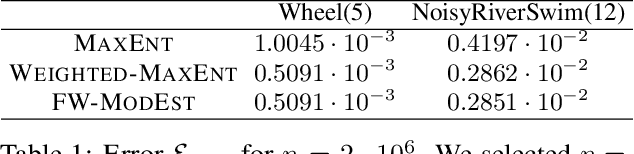
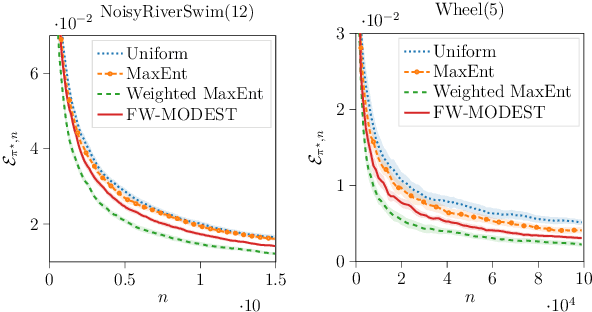
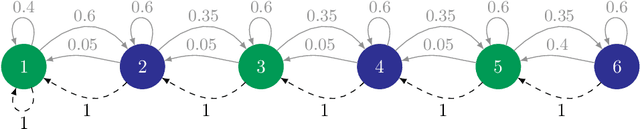
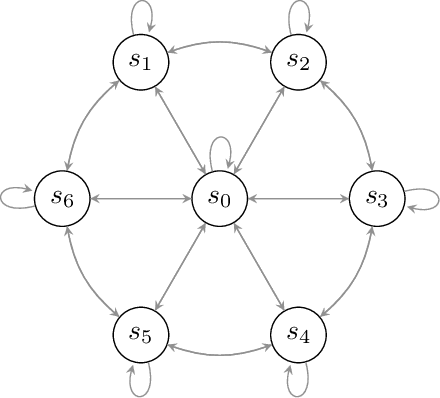
We study the problem of efficient exploration in order to learn an accurate model of an environment, modeled as a Markov decision process (MDP). Efficient exploration in this problem requires the agent to identify the regions in which estimating the model is more difficult and then exploit this knowledge to collect more samples there. In this paper, we formalize this problem, introduce the first algorithm to learn an $\epsilon$-accurate estimate of the dynamics, and provide its sample complexity analysis. While this algorithm enjoys strong guarantees in the large-sample regime, it tends to have a poor performance in early stages of exploration. To address this issue, we propose an algorithm that is based on maximum weighted entropy, a heuristic that stems from common sense and our theoretical analysis. The main idea here is cover the entire state-action space with the weight proportional to the noise in the transitions. Using a number of simple domains with heterogeneous noise in their transitions, we show that our heuristic-based algorithm outperforms both our original algorithm and the maximum entropy algorithm in the small sample regime, while achieving similar asymptotic performance as that of the original algorithm.

Exploration-Exploitation in Constrained MDPs

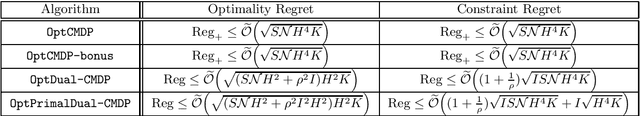
In many sequential decision-making problems, the goal is to optimize a utility function while satisfying a set of constraints on different utilities. This learning problem is formalized through Constrained Markov Decision Processes (CMDPs). In this paper, we investigate the exploration-exploitation dilemma in CMDPs. While learning in an unknown CMDP, an agent should trade-off exploration to discover new information about the MDP, and exploitation of the current knowledge to maximize the reward while satisfying the constraints. While the agent will eventually learn a good or optimal policy, we do not want the agent to violate the constraints too often during the learning process. In this work, we analyze two approaches for learning in CMDPs. The first approach leverages the linear formulation of CMDP to perform optimistic planning at each episode. The second approach leverages the dual formulation (or saddle-point formulation) of CMDP to perform incremental, optimistic updates of the primal and dual variables. We show that both achieves sublinear regret w.r.t.\ the main utility while having a sublinear regret on the constraint violations. That being said, we highlight a crucial difference between the two approaches; the linear programming approach results in stronger guarantees than in the dual formulation based approach.

Adversarial Attacks on Linear Contextual Bandits

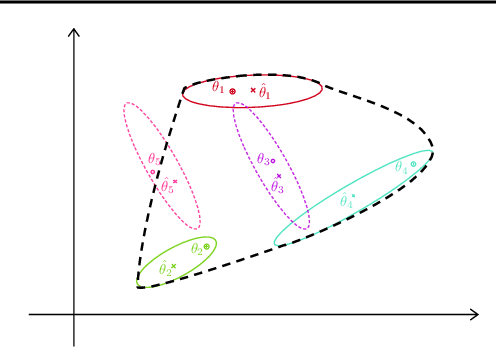
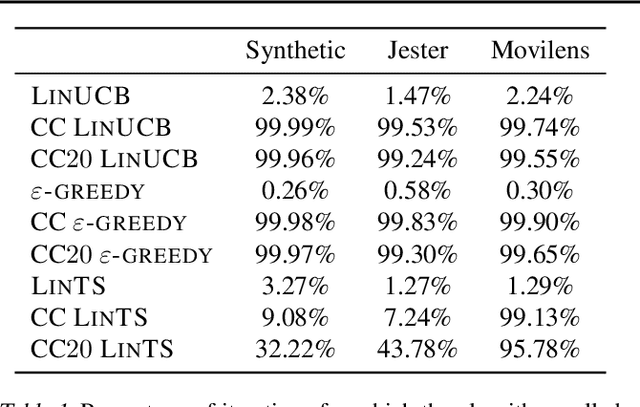
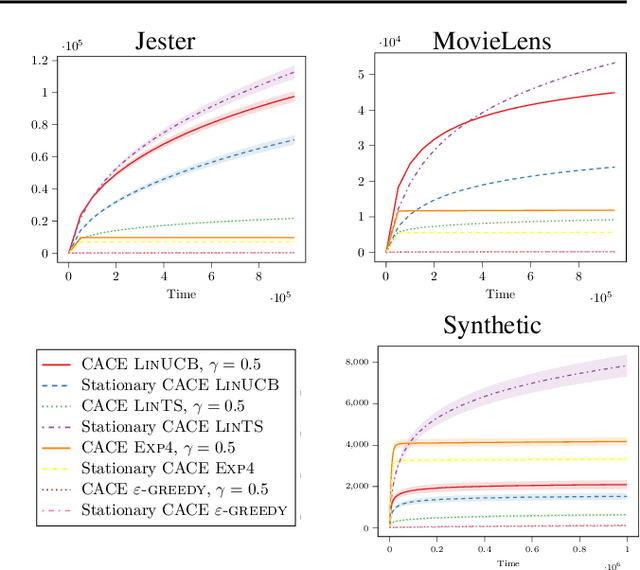
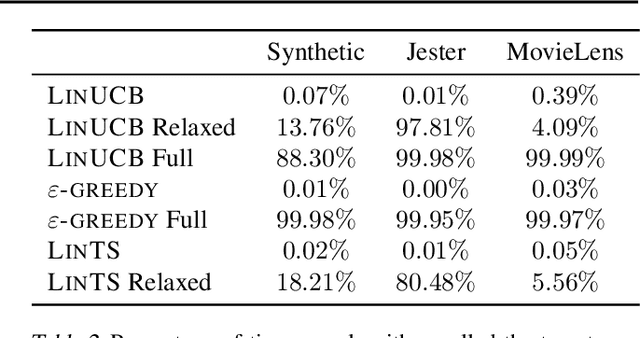
Contextual bandit algorithms are applied in a wide range of domains, from advertising to recommender systems, from clinical trials to education. In many of these domains, malicious agents may have incentives to attack the bandit algorithm to induce it to perform a desired behavior. For instance, an unscrupulous ad publisher may try to increase their own revenue at the expense of the advertisers; a seller may want to increase the exposure of their products, or thwart a competitor's advertising campaign. In this paper, we study several attack scenarios and show that a malicious agent can force a linear contextual bandit algorithm to pull any desired arm $T - o(T)$ times over a horizon of $T$ steps, while applying adversarial modifications to either rewards or contexts that only grow logarithmically as $O(\log T)$. We also investigate the case when a malicious agent is interested in affecting the behavior of the bandit algorithm in a single context (e.g., a specific user). We first provide sufficient conditions for the feasibility of the attack and we then propose an efficient algorithm to perform the attack. We validate our theoretical results on experiments performed on both synthetic and real-world datasets.

Improved Algorithms for Conservative Exploration in Bandits

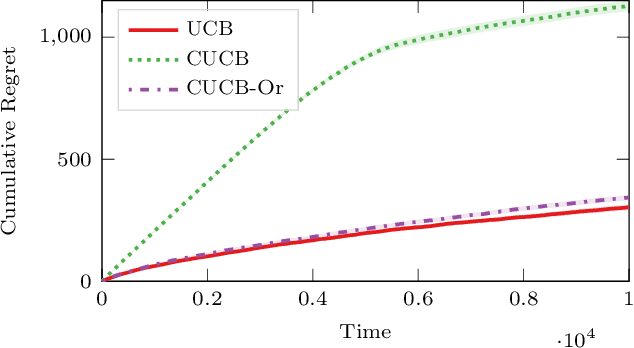
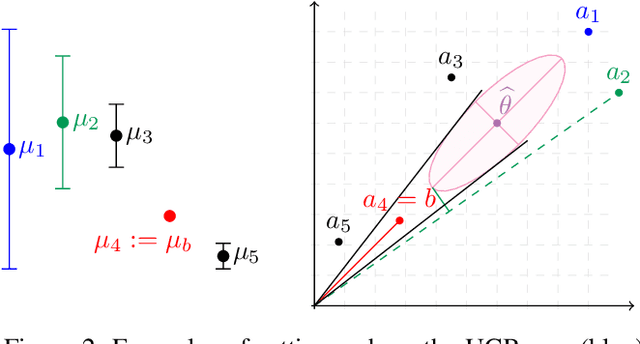
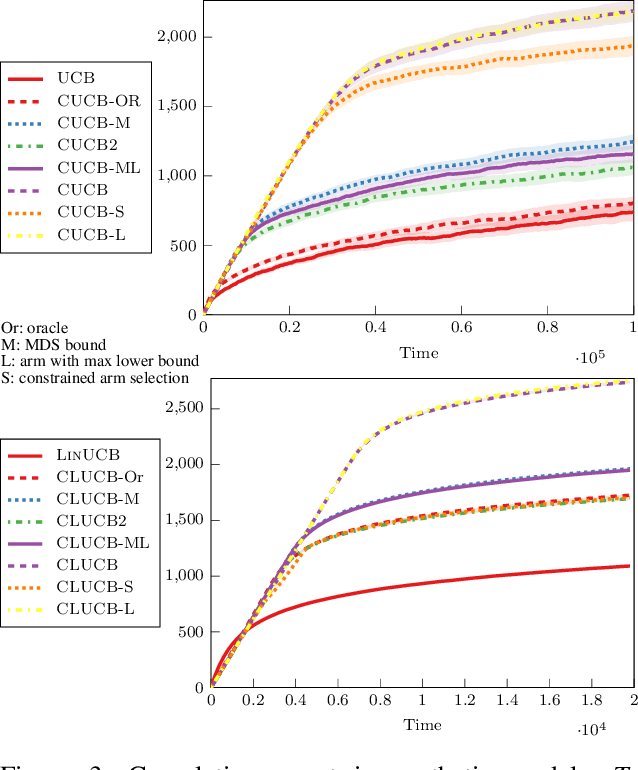
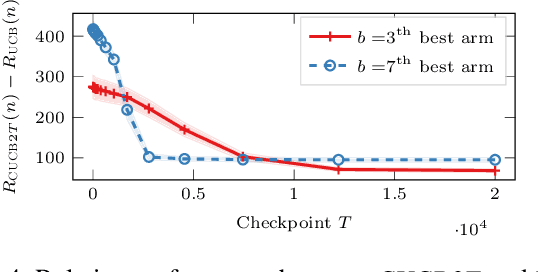
In many fields such as digital marketing, healthcare, finance, and robotics, it is common to have a well-tested and reliable baseline policy running in production (e.g., a recommender system). Nonetheless, the baseline policy is often suboptimal. In this case, it is desirable to deploy online learning algorithms (e.g., a multi-armed bandit algorithm) that interact with the system to learn a better/optimal policy under the constraint that during the learning process the performance is almost never worse than the performance of the baseline itself. In this paper, we study the conservative learning problem in the contextual linear bandit setting and introduce a novel algorithm, the Conservative Constrained LinUCB (CLUCB2). We derive regret bounds for CLUCB2 that match existing results and empirically show that it outperforms state-of-the-art conservative bandit algorithms in a number of synthetic and real-world problems. Finally, we consider a more realistic constraint where the performance is verified only at predefined checkpoints (instead of at every step) and show how this relaxed constraint favorably impacts the regret and empirical performance of CLUCB2.

Conservative Exploration in Reinforcement Learning

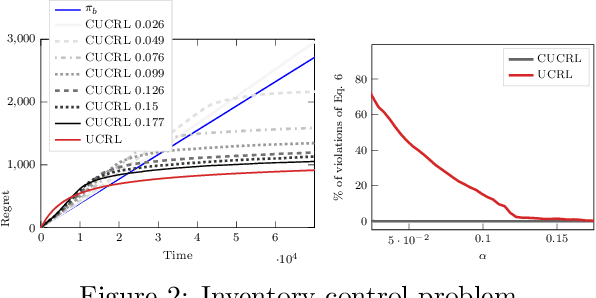
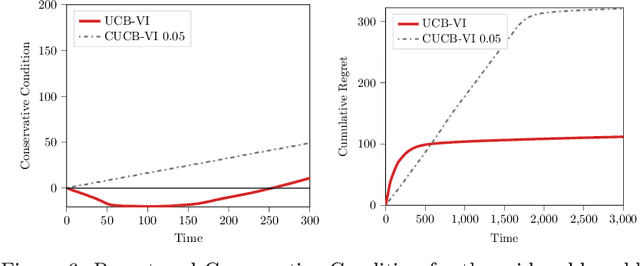
While learning in an unknown Markov Decision Process (MDP), an agent should trade off exploration to discover new information about the MDP, and exploitation of the current knowledge to maximize the reward. Although the agent will eventually learn a good or optimal policy, there is no guarantee on the quality of the intermediate policies. This lack of control is undesired in real-world applications where a minimum requirement is that the executed policies are guaranteed to perform at least as well as an existing baseline. In this paper, we introduce the notion of conservative exploration for average reward and finite horizon problems. We present two optimistic algorithms that guarantee (w.h.p.) that the conservative constraint is never violated during learning. We derive regret bounds showing that being conservative does not hinder the learning ability of these algorithms.

Concentration Inequalities for Multinoulli Random Variables

We investigate concentration inequalities for Dirichlet and Multinomial random variables.

No-Regret Exploration in Goal-Oriented Reinforcement Learning

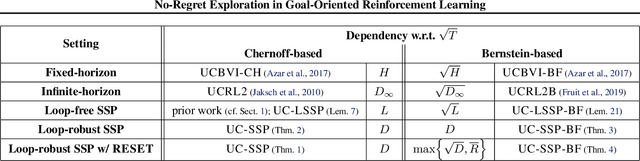
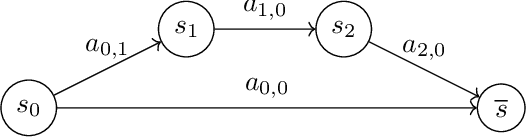
Many popular reinforcement learning problems (e.g., navigation in a maze, some Atari games, mountain car) are instances of the episodic setting under its stochastic shortest path (SSP) formulation, where an agent has to achieve a goal state while minimizing the cumulative cost. Despite the popularity of this setting, the exploration-exploitation dilemma has been sparsely studied in general SSP problems, with most of the theoretical literature focusing on different problems (i.e., fixed-horizon and infinite-horizon) or making the restrictive loop-free SSP assumption (i.e., no state can be visited twice during an episode). In this paper, we study the general SSP problem with no assumption on its dynamics (some policies may actually never reach the goal). We introduce UC-SSP, the first no-regret algorithm in this setting, and prove a regret bound scaling as $\displaystyle \widetilde{\mathcal{O}}( D S \sqrt{ A D K})$ after $K$ episodes for any unknown SSP with $S$ states, $A$ actions, positive costs and SSP-diameter $D$, defined as the smallest expected hitting time from any starting state to the goal. We achieve this result by crafting a novel stopping rule, such that UC-SSP may interrupt the current policy if it is taking too long to achieve the goal and switch to alternative policies that are designed to rapidly terminate the episode.

Exploiting Language Instructions for Interpretable and Compositional Reinforcement Learning

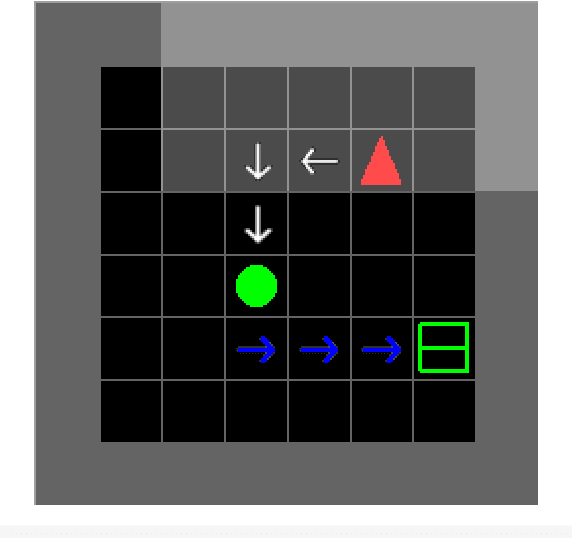
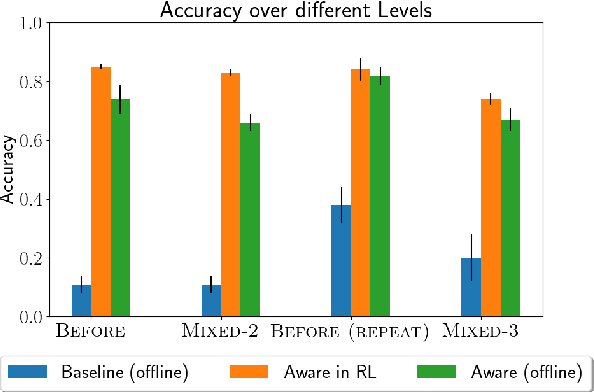
In this work, we present an alternative approach to making an agent compositional through the use of a diagnostic classifier. Because of the need for explainable agents in automated decision processes, we attempt to interpret the latent space from an RL agent to identify its current objective in a complex language instruction. Results show that the classification process causes changes in the hidden states which makes them more easily interpretable, but also causes a shift in zero-shot performance to novel instructions. Lastly, we limit the supervisory signal on the classification, and observe a similar but less notable effect.

Frequentist Regret Bounds for Randomized Least-Squares Value Iteration

We consider the exploration-exploitation dilemma in finite-horizon reinforcement learning (RL). When the state space is large or continuous, traditional tabular approaches are unfeasible and some form of function approximation is mandatory. In this paper, we introduce an optimistically-initialized variant of the popular randomized least-squares value iteration (RLSVI), a model-free algorithm where exploration is induced by perturbing the least-squares approximation of the action-value function. Under the assumption that the Markov decision process has low-rank transition dynamics, we prove that the frequentist regret of RLSVI is upper-bounded by $\widetilde O(d^2 H^2 \sqrt{T})$ where $ d $ are the feature dimension, $ H $ is the horizon, and $ T $ is the total number of steps. To the best of our knowledge, this is the first frequentist regret analysis for randomized exploration with function approximation.