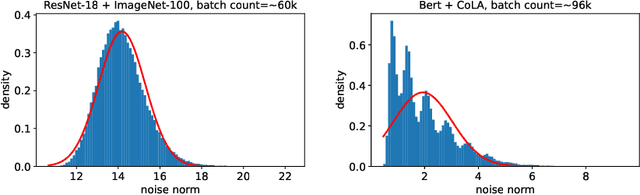
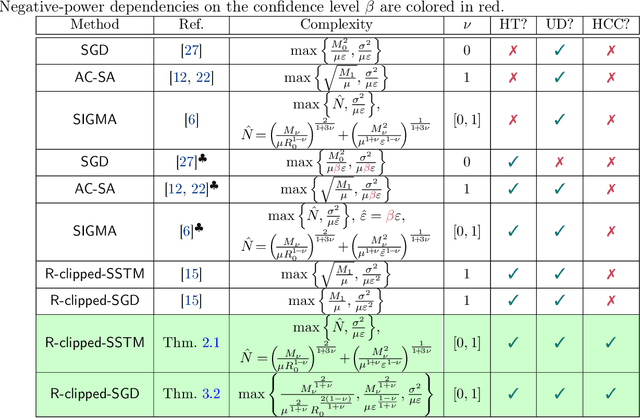
High-Probability Convergence for Composite and Distributed Stochastic Minimization and Variational Inequalities with Heavy-Tailed Noise

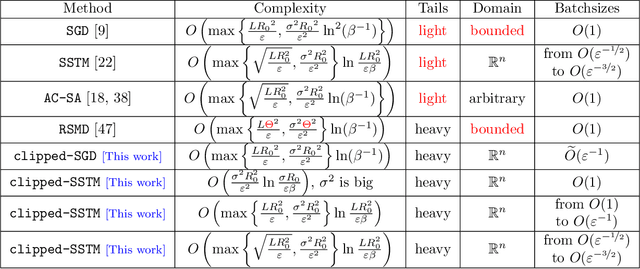
High-probability analysis of stochastic first-order optimization methods under mild assumptions on the noise has been gaining a lot of attention in recent years. Typically, gradient clipping is one of the key algorithmic ingredients to derive good high-probability guarantees when the noise is heavy-tailed. However, if implemented na\"ively, clipping can spoil the convergence of the popular methods for composite and distributed optimization (Prox-SGD/Parallel SGD) even in the absence of any noise. Due to this reason, many works on high-probability analysis consider only unconstrained non-distributed problems, and the existing results for composite/distributed problems do not include some important special cases (like strongly convex problems) and are not optimal. To address this issue, we propose new stochastic methods for composite and distributed optimization based on the clipping of stochastic gradient differences and prove tight high-probability convergence results (including nearly optimal ones) for the new methods. Using similar ideas, we also develop new methods for composite and distributed variational inequalities and analyze the high-probability convergence of these methods.

High-Probability Bounds for Stochastic Optimization and Variational Inequalities: the Case of Unbounded Variance

During recent years the interest of optimization and machine learning communities in high-probability convergence of stochastic optimization methods has been growing. One of the main reasons for this is that high-probability complexity bounds are more accurate and less studied than in-expectation ones. However, SOTA high-probability non-asymptotic convergence results are derived under strong assumptions such as the boundedness of the gradient noise variance or of the objective's gradient itself. In this paper, we propose several algorithms with high-probability convergence results under less restrictive assumptions. In particular, we derive new high-probability convergence results under the assumption that the gradient/operator noise has bounded central $\alpha$-th moment for $\alpha \in (1,2]$ in the following setups: (i) smooth non-convex / Polyak-Lojasiewicz / convex / strongly convex / quasi-strongly convex minimization problems, (ii) Lipschitz / star-cocoercive and monotone / quasi-strongly monotone variational inequalities. These results justify the usage of the considered methods for solving problems that do not fit standard functional classes studied in stochastic optimization.

Clipped Stochastic Methods for Variational Inequalities with Heavy-Tailed Noise

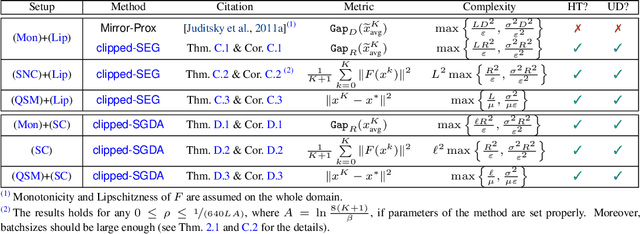
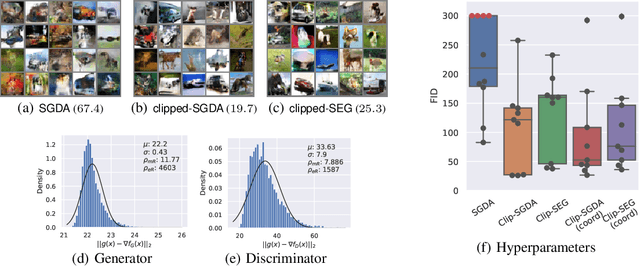
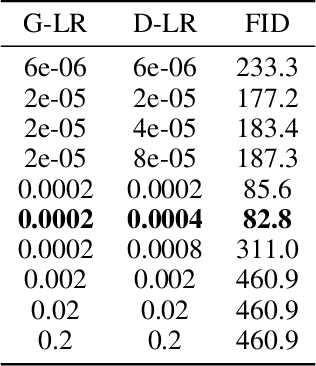
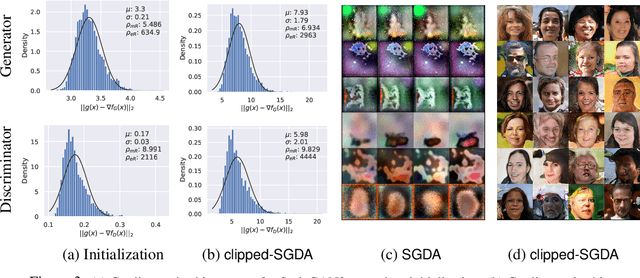
Stochastic first-order methods such as Stochastic Extragradient (SEG) or Stochastic Gradient Descent-Ascent (SGDA) for solving smooth minimax problems and, more generally, variational inequality problems (VIP) have been gaining a lot of attention in recent years due to the growing popularity of adversarial formulations in machine learning. However, while high-probability convergence bounds are known to reflect the actual behavior of stochastic methods more accurately, most convergence results are provided in expectation. Moreover, the only known high-probability complexity results have been derived under restrictive sub-Gaussian (light-tailed) noise and bounded domain Assump. [Juditsky et al., 2011]. In this work, we prove the first high-probability complexity results with logarithmic dependence on the confidence level for stochastic methods for solving monotone and structured non-monotone VIPs with non-sub-Gaussian (heavy-tailed) noise and unbounded domains. In the monotone case, our results match the best-known ones in the light-tails case [Juditsky et al., 2011], and are novel for structured non-monotone problems such as negative comonotone, quasi-strongly monotone, and/or star-cocoercive ones. We achieve these results by studying SEG and SGDA with clipping. In addition, we numerically validate that the gradient noise of many practical GAN formulations is heavy-tailed and show that clipping improves the performance of SEG/SGDA.

Distributed Methods with Absolute Compression and Error Compensation

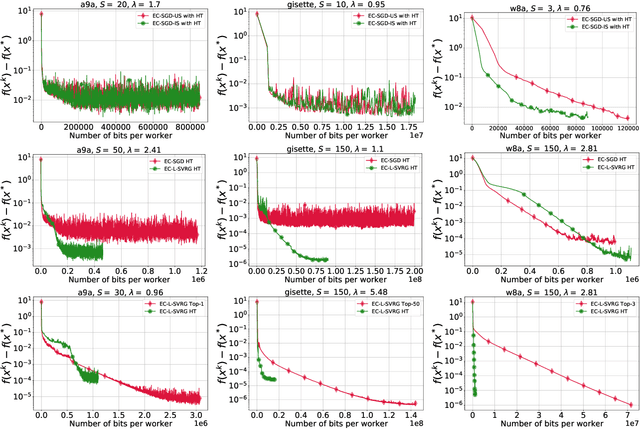
Distributed optimization methods are often applied to solving huge-scale problems like training neural networks with millions and even billions of parameters. In such applications, communicating full vectors, e.g., (stochastic) gradients, iterates, is prohibitively expensive, especially when the number of workers is large. Communication compression is a powerful approach to alleviating this issue, and, in particular, methods with biased compression and error compensation are extremely popular due to their practical efficiency. Sahu et al. (2021) propose a new analysis of Error Compensated SGD (EC-SGD) for the class of absolute compression operators showing that in a certain sense, this class contains optimal compressors for EC-SGD. However, the analysis was conducted only under the so-called $(M,\sigma^2)$-bounded noise assumption. In this paper, we generalize the analysis of EC-SGD with absolute compression to the arbitrary sampling strategy and propose the first analysis of EC-LSVRG with absolute compression for (strongly) convex problems. Our rates improve upon the previously known ones in this setting. Our theoretical findings are corroborated by several numerical experiments.

Near-Optimal High Probability Complexity Bounds for Non-Smooth Stochastic Optimization with Heavy-Tailed Noise

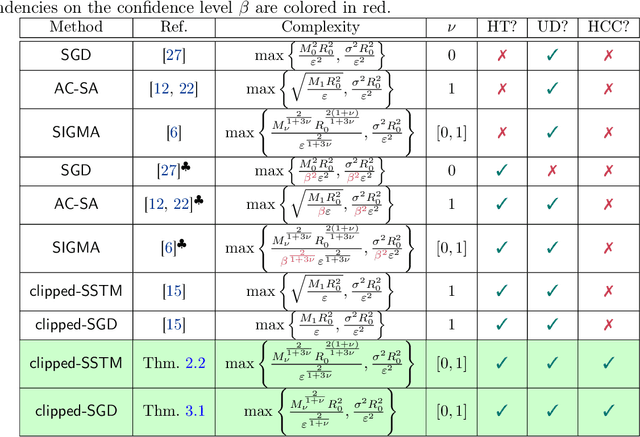
Thanks to their practical efficiency and random nature of the data, stochastic first-order methods are standard for training large-scale machine learning models. Random behavior may cause a particular run of an algorithm to result in a highly suboptimal objective value, whereas theoretical guarantees are usually proved for the expectation of the objective value. Thus, it is essential to theoretically guarantee that algorithms provide small objective residual with high probability. Existing methods for non-smooth stochastic convex optimization have complexity bounds with the dependence on the confidence level that is either negative-power or logarithmic but under an additional assumption of sub-Gaussian (light-tailed) noise distribution that may not hold in practice, e.g., in several NLP tasks. In our paper, we resolve this issue and derive the first high-probability convergence results with logarithmic dependence on the confidence level for non-smooth convex stochastic optimization problems with non-sub-Gaussian (heavy-tailed) noise. To derive our results, we propose novel stepsize rules for two stochastic methods with gradient clipping. Moreover, our analysis works for generalized smooth objectives with H\"older-continuous gradients, and for both methods, we provide an extension for strongly convex problems. Finally, our results imply that the first (accelerated) method we consider also has optimal iteration and oracle complexity in all the regimes, and the second one is optimal in the non-smooth setting.

Recent Theoretical Advances in Non-Convex Optimization

Motivated by recent increased interest in optimization algorithms for non-convex optimization in application to training deep neural networks and other optimization problems in data analysis, we give an overview of recent theoretical results on global performance guarantees of optimization algorithms for non-convex optimization. We start with classical arguments showing that general non-convex problems could not be solved efficiently in a reasonable time. Then we give a list of problems that can be solved efficiently to find the global minimizer by exploiting the structure of the problem as much as it is possible. Another way to deal with non-convexity is to relax the goal from finding the global minimum to finding a stationary point or a local minimum. For this setting, we first present known results for the convergence rates of deterministic first-order methods, which are then followed by a general theoretical analysis of optimal stochastic and randomized gradient schemes, and an overview of the stochastic first-order methods. After that, we discuss quite general classes of non-convex problems, such as minimization of $\alpha$-weakly-quasi-convex functions and functions that satisfy Polyak--Lojasiewicz condition, which still allow obtaining theoretical convergence guarantees of first-order methods. Then we consider higher-order and zeroth-order/derivative-free methods and their convergence rates for non-convex optimization problems.

Stochastic Optimization with Heavy-Tailed Noise via Accelerated Gradient Clipping

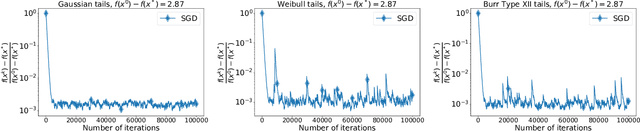
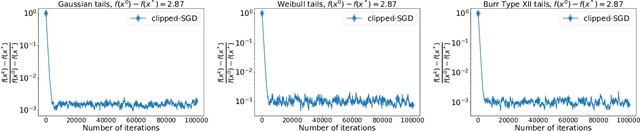
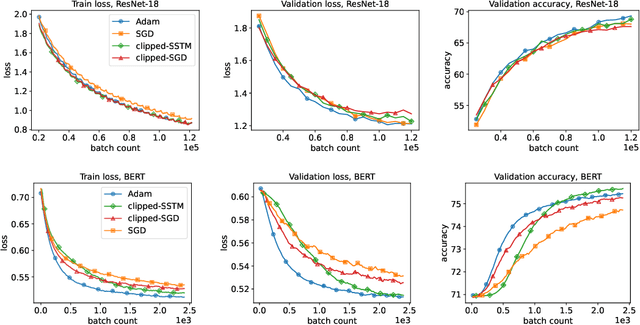
In this paper, we propose a new accelerated stochastic first-order method called clipped-SSTM for smooth convex stochastic optimization with heavy-tailed distributed noise in stochastic gradients and derive the first high-probability complexity bounds for this method closing the gap in the theory of stochastic optimization with heavy-tailed noise. Our method is based on a special variant of accelerated Stochastic Gradient Descent (SGD) and clipping of stochastic gradients. We extend our method to the strongly convex case and prove new complexity bounds that outperform state-of-the-art results in this case. Finally, we extend our proof technique and derive the first non-trivial high-probability complexity bounds for SGD with clipping without light-tails assumption on the noise.