Weak Collocation Regression for Inferring Stochastic Dynamics with Lévy Noise

With the rapid increase of observational, experimental and simulated data for stochastic systems, tremendous efforts have been devoted to identifying governing laws underlying the evolution of these systems. Despite the broad applications of non-Gaussian fluctuations in numerous physical phenomena, the data-driven approaches to extracting stochastic dynamics with L\'{e}vy noise are relatively few. In this work, we propose a Weak Collocation Regression (WCR) to explicitly reveal unknown stochastic dynamical systems, i.e., the Stochastic Differential Equation (SDE) with both $\alpha$-stable L\'{e}vy noise and Gaussian noise, from discrete aggregate data. This method utilizes the evolution equation of the probability distribution function, i.e., the Fokker-Planck (FP) equation. With the weak form of the FP equation, the WCR constructs a linear system of unknown parameters where all integrals are evaluated by Monte Carlo method with the observations. Then, the unknown parameters are obtained by a sparse linear regression. For a SDE with L\'{e}vy noise, the corresponding FP equation is a partial integro-differential equation (PIDE), which contains nonlocal terms, and is difficult to deal with. The weak form can avoid complicated multiple integrals. Our approach can simultaneously distinguish mixed noise types, even in multi-dimensional problems. Numerical experiments demonstrate that our method is accurate and computationally efficient.

Temporal Difference Learning for High-Dimensional PIDEs with Jumps

In this paper, we propose a deep learning framework for solving high-dimensional partial integro-differential equations (PIDEs) based on the temporal difference learning. We introduce a set of Levy processes and construct a corresponding reinforcement learning model. To simulate the entire process, we use deep neural networks to represent the solutions and non-local terms of the equations. Subsequently, we train the networks using the temporal difference error, termination condition, and properties of the non-local terms as the loss function. The relative error of the method reaches O(10^{-3}) in 100-dimensional experiments and O(10^{-4}) in one-dimensional pure jump problems. Additionally, our method demonstrates the advantages of low computational cost and robustness, making it well-suited for addressing problems with different forms and intensities of jumps.

Weak Collocation Regression method: fast reveal hidden stochastic dynamics from high-dimensional aggregate data

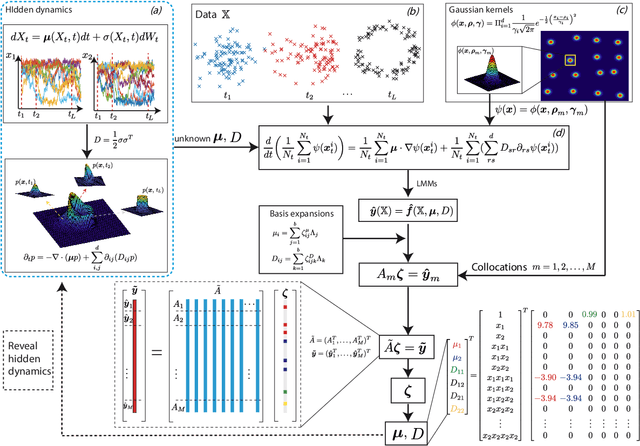
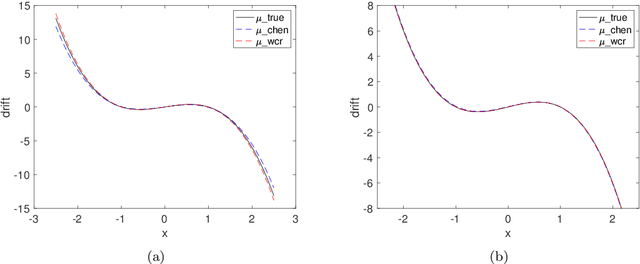
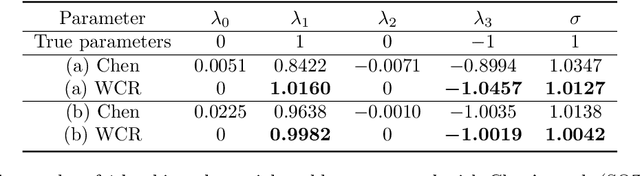
Revealing hidden dynamics from the stochastic data is a challenging problem as randomness takes part in the evolution of the data. The problem becomes exceedingly complex when the trajectories of the stochastic data are absent in many scenarios. Here we present an approach to effectively modeling the dynamics of the stochastic data without trajectories based on the weak form of the Fokker-Planck (FP) equation, which governs the evolution of the density function in the Brownian process. Taking the collocations of Gaussian functions as the test functions in the weak form of the FP equation, we transfer the derivatives to the Gaussian functions and thus approximate the weak form by the expectational sum of the data. With a dictionary representation of the unknown terms, a linear system is built and then solved by the regression, revealing the unknown dynamics of the data. Hence, we name the method with the Weak Collocation Regression (WCR) method for its three key components: weak form, collocation of Gaussian kernels, and regression. The numerical experiments show that our method is flexible and fast, which reveals the dynamics within seconds in multi-dimensional problems and can be easily extended to high-dimensional data such as 20 dimensions. WCR can also correctly identify the hidden dynamics of the complex tasks with variable-dependent diffusion and coupled drift, and the performance is robust, achieving high accuracy in the case with noise added.