Depthwise Convolution is All You Need for Learning Multiple Visual Domains

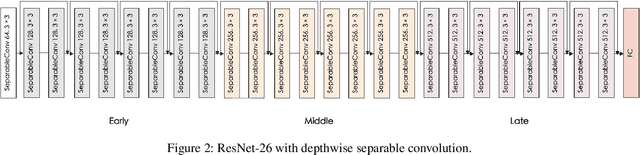
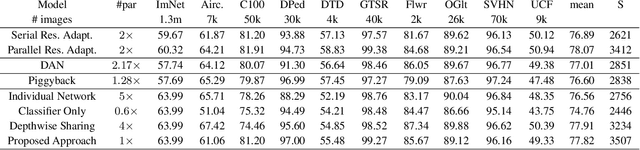
There is a growing interest in designing models that can deal with images from different visual domains. If there exists a universal structure in different visual domains that can be captured via a common parameterization, then we can use a single model for all domains rather than one model per domain. A model aware of the relationships between different domains can also be trained to work on new domains with less resources. However, to identify the reusable structure in a model is not easy. In this paper, we propose a multi-domain learning architecture based on depthwise separable convolution. The proposed approach is based on the assumption that images from different domains share cross-channel correlations but have domain-specific spatial correlations. The proposed model is compact and has minimal overhead when being applied to new domains. Additionally, we introduce a gating mechanism to promote soft sharing between different domains. We evaluate our approach on Visual Decathlon Challenge, a benchmark for testing the ability of multi-domain models. The experiments show that our approach can achieve the highest score while only requiring 50% of the parameters compared with the state-of-the-art approaches.

Learning to Adaptively Scale Recurrent Neural Networks

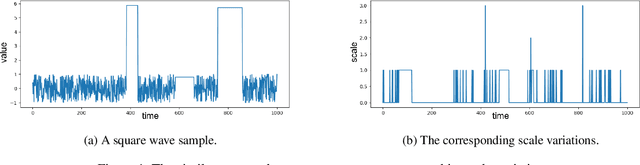
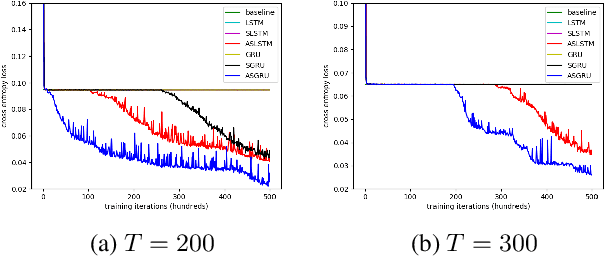
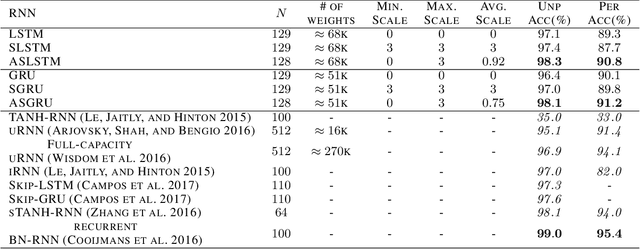
Recent advancements in recurrent neural network (RNN) research have demonstrated the superiority of utilizing multiscale structures in learning temporal representations of time series. Currently, most of multiscale RNNs use fixed scales, which do not comply with the nature of dynamical temporal patterns among sequences. In this paper, we propose Adaptively Scaled Recurrent Neural Networks (ASRNN), a simple but efficient way to handle this problem. Instead of using predefined scales, ASRNNs are able to learn and adjust scales based on different temporal contexts, making them more flexible in modeling multiscale patterns. Compared with other multiscale RNNs, ASRNNs are bestowed upon dynamical scaling capabilities with much simpler structures, and are easy to be integrated with various RNN cells. The experiments on multiple sequence modeling tasks indicate ASRNNs can efficiently adapt scales based on different sequence contexts and yield better performances than baselines without dynamical scaling abilities.

Asynchronous Delay-Aware Accelerated Proximal Coordinate Descent for Nonconvex Nonsmooth Problems

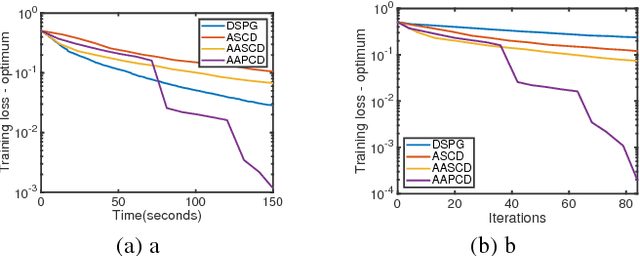
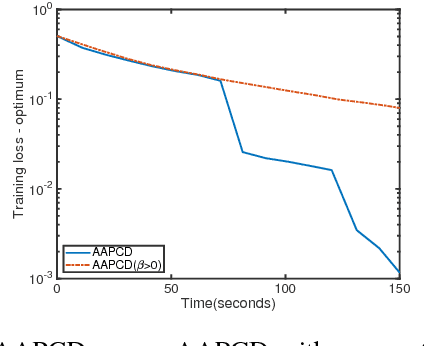
Nonconvex and nonsmooth problems have recently attracted considerable attention in machine learning. However, developing efficient methods for the nonconvex and nonsmooth optimization problems with certain performance guarantee remains a challenge. Proximal coordinate descent (PCD) has been widely used for solving optimization problems, but the knowledge of PCD methods in the nonconvex setting is very limited. On the other hand, the asynchronous proximal coordinate descent (APCD) recently have received much attention in order to solve large-scale problems. However, the accelerated variants of APCD algorithms are rarely studied. In this paper, we extend APCD method to the accelerated algorithm (AAPCD) for nonsmooth and nonconvex problems that satisfies the sufficient descent property, by comparing between the function values at proximal update and a linear extrapolated point using a delay-aware momentum value. To the best of our knowledge, we are the first to provide stochastic and deterministic accelerated extension of APCD algorithms for general nonconvex and nonsmooth problems ensuring that for both bounded delays and unbounded delays every limit point is a critical point. By leveraging Kurdyka-Lojasiewicz property, we will show linear and sublinear convergence rates for the deterministic AAPCD with bounded delays. Numerical results demonstrate the practical efficiency of our algorithm in speed.

AET vs. AED: Unsupervised Representation Learning by Auto-Encoding Transformations rather than Data

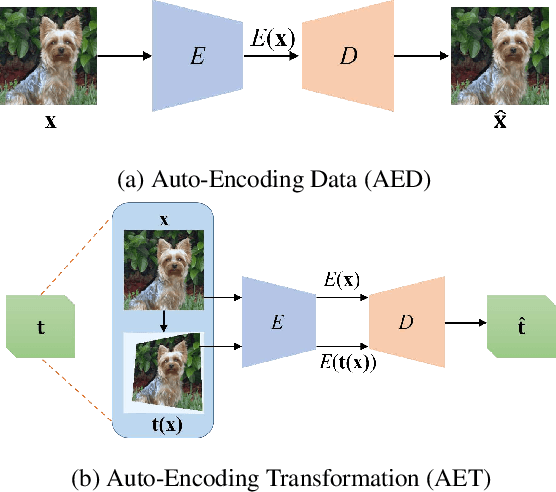
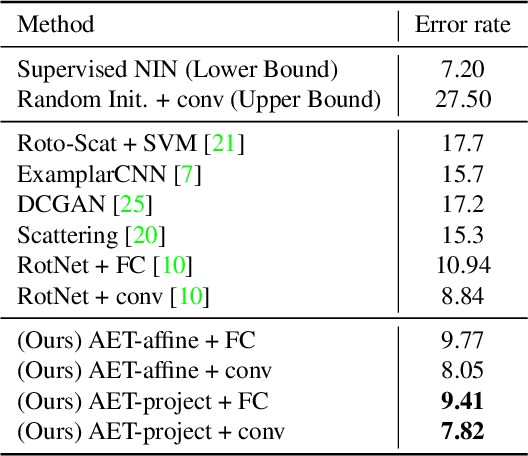
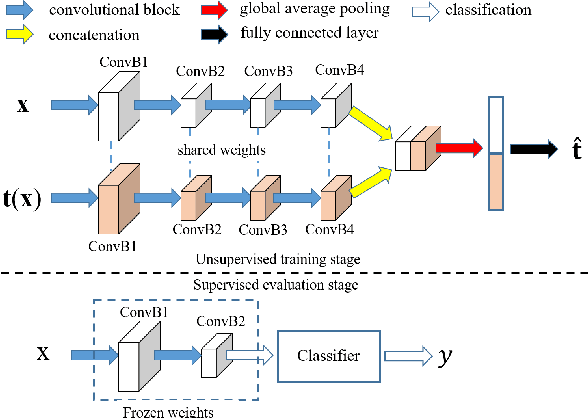
The success of deep neural networks often relies on a large amount of labeled examples, which can be difficult to obtain in many real scenarios. To address this challenge, unsupervised methods are strongly preferred for training neural networks without using any labeled data. In this paper, we present a novel paradigm of unsupervised representation learning by Auto-Encoding Transformation (AET) in contrast to the conventional Auto-Encoding Data (AED) approach. Given a randomly sampled transformation, AET seeks to predict it merely from the encoded features as accurately as possible at the output end. The idea is the following: as long as the unsupervised features successfully encode the essential information about the visual structures of original and transformed images, the transformation can be well predicted. We will show that this AET paradigm allows us to instantiate a large variety of transformations, from parameterized, to non-parameterized and GAN-induced ones. Our experiments show that AET greatly improves over existing unsupervised approaches, setting new state-of-the-art performances being greatly closer to the upper bounds by their fully supervised counterparts on CIFAR-10, ImageNet and Places datasets.

A Proximal Zeroth-Order Algorithm for Nonconvex Nonsmooth Problems

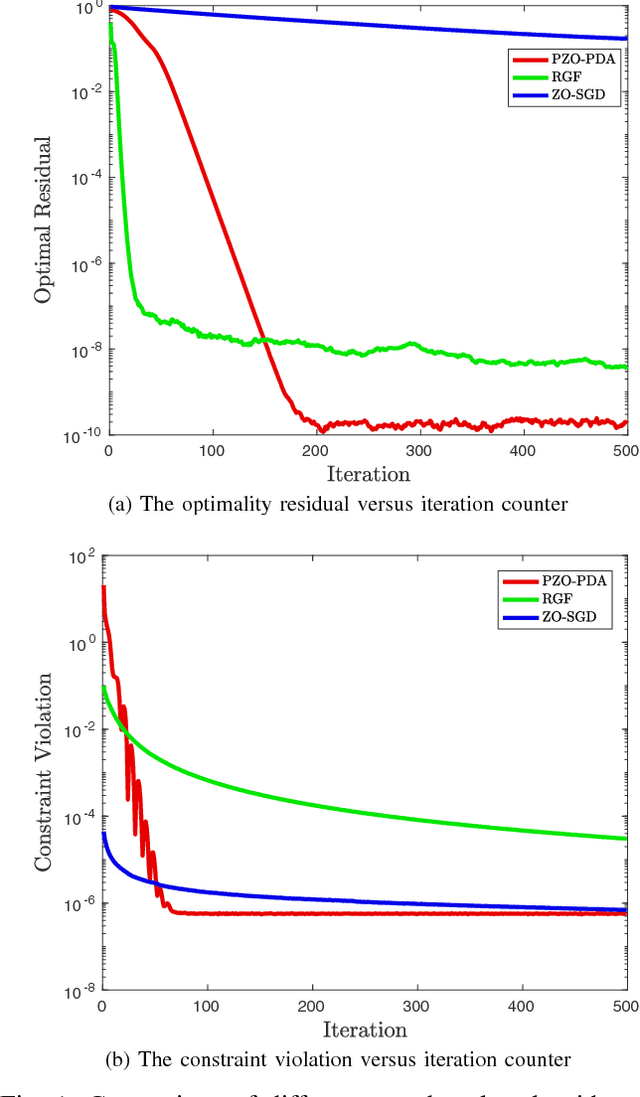
In this paper, we focus on solving an important class of nonconvex optimization problems which includes many problems for example signal processing over a networked multi-agent system and distributed learning over networks. Motivated by many applications in which the local objective function is the sum of smooth but possibly nonconvex part, and non-smooth but convex part subject to a linear equality constraint, this paper proposes a proximal zeroth-order primal dual algorithm (PZO-PDA) that accounts for the information structure of the problem. This algorithm only utilize the zeroth-order information (i.e., the functional values) of smooth functions, yet the flexibility is achieved for applications that only noisy information of the objective function is accessible, where classical methods cannot be applied. We prove convergence and rate of convergence for PZO-PDA. Numerical experiments are provided to validate the theoretical results.

How Local is the Local Diversity? Reinforcing Sequential Determinantal Point Processes with Dynamic Ground Sets for Supervised Video Summarization

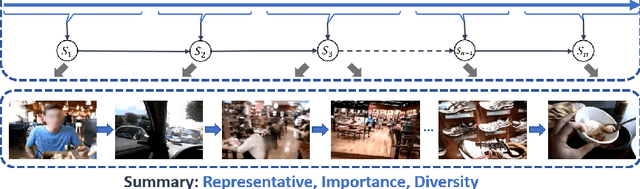
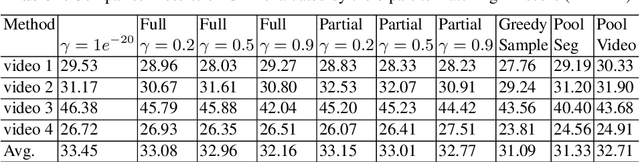
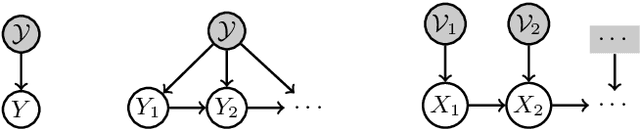
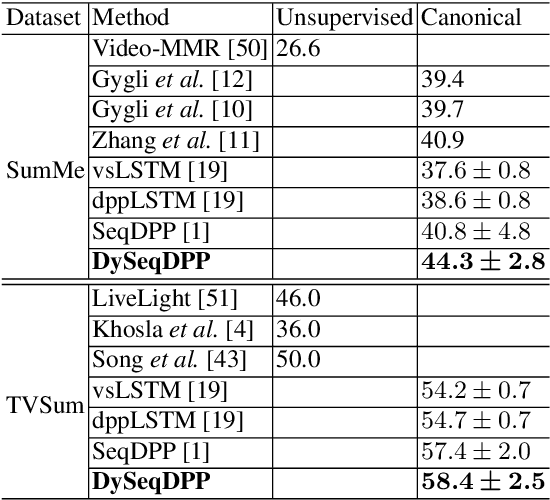
The large volume of video content and high viewing frequency demand automatic video summarization algorithms, of which a key property is the capability of modeling diversity. If videos are lengthy like hours-long egocentric videos, it is necessary to track the temporal structures of the videos and enforce local diversity. The local diversity refers to that the shots selected from a short time duration are diverse but visually similar shots are allowed to co-exist in the summary if they appear far apart in the video. In this paper, we propose a novel probabilistic model, built upon SeqDPP, to dynamically control the time span of a video segment upon which the local diversity is imposed. In particular, we enable SeqDPP to learn to automatically infer how local the local diversity is supposed to be from the input video. The resulting model is extremely involved to train by the hallmark maximum likelihood estimation (MLE), which further suffers from the exposure bias and non-differentiable evaluation metrics. To tackle these problems, we instead devise a reinforcement learning algorithm for training the proposed model. Extensive experiments verify the advantages of our model and the new learning algorithm over MLE-based methods.

A Semi-Supervised Two-Stage Approach to Learning from Noisy Labels

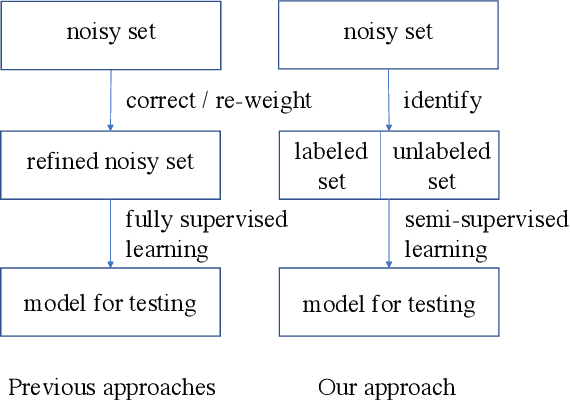
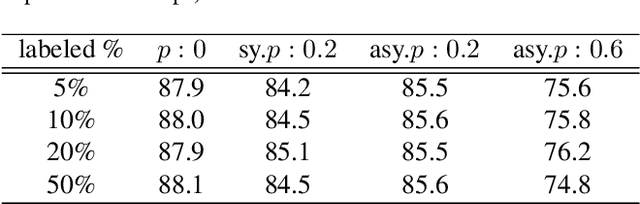
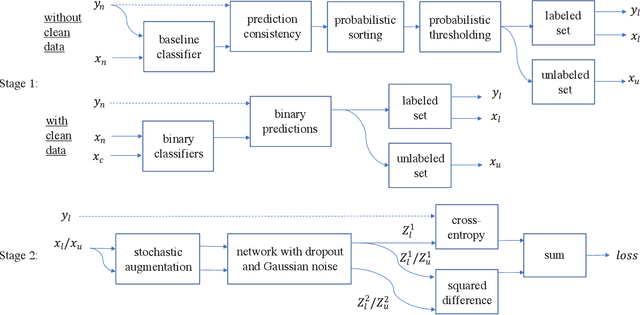
The recent success of deep neural networks is powered in part by large-scale well-labeled training data. However, it is a daunting task to laboriously annotate an ImageNet-like dateset. On the contrary, it is fairly convenient, fast, and cheap to collect training images from the Web along with their noisy labels. This signifies the need of alternative approaches to training deep neural networks using such noisy labels. Existing methods tackling this problem either try to identify and correct the wrong labels or reweigh the data terms in the loss function according to the inferred noisy rates. Both strategies inevitably incur errors for some of the data points. In this paper, we contend that it is actually better to ignore the labels of some of the data points than to keep them if the labels are incorrect, especially when the noisy rate is high. After all, the wrong labels could mislead a neural network to a bad local optimum. We suggest a two-stage framework for the learning from noisy labels. In the first stage, we identify a small portion of images from the noisy training set of which the labels are correct with a high probability. The noisy labels of the other images are ignored. In the second stage, we train a deep neural network in a semi-supervised manner. This framework effectively takes advantage of the whole training set and yet only a portion of its labels that are most likely correct. Experiments on three datasets verify the effectiveness of our approach especially when the noisy rate is high.

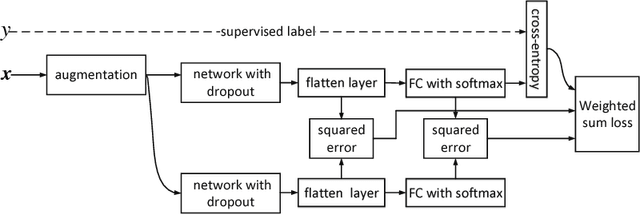
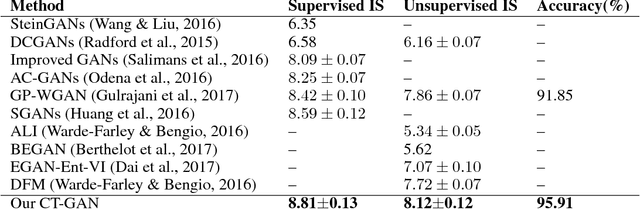
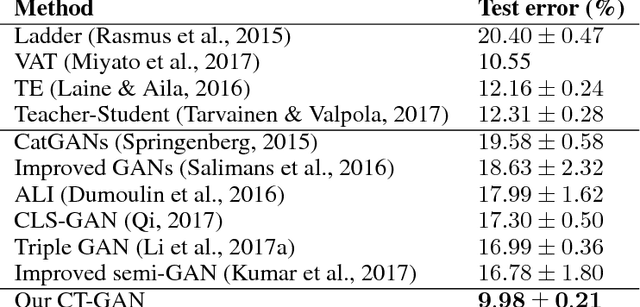
Improving the Improved Training of Wasserstein GANs: A Consistency Term and Its Dual Effect

Despite being impactful on a variety of problems and applications, the generative adversarial nets (GANs) are remarkably difficult to train. This issue is formally analyzed by \cite{arjovsky2017towards}, who also propose an alternative direction to avoid the caveats in the minmax two-player training of GANs. The corresponding algorithm, called Wasserstein GAN (WGAN), hinges on the 1-Lipschitz continuity of the discriminator. In this paper, we propose a novel approach to enforcing the Lipschitz continuity in the training procedure of WGANs. Our approach seamlessly connects WGAN with one of the recent semi-supervised learning methods. As a result, it gives rise to not only better photo-realistic samples than the previous methods but also state-of-the-art semi-supervised learning results. In particular, our approach gives rise to the inception score of more than 5.0 with only 1,000 CIFAR-10 images and is the first that exceeds the accuracy of 90% on the CIFAR-10 dataset using only 4,000 labeled images, to the best of our knowledge.