Expand Neurons, Not Parameters

This work demonstrates how increasing the number of neurons in a network without increasing its number of non-zero parameters improves performance. We show that this gain corresponds with a decrease in interference between multiple features that would otherwise share the same neurons. To reduce such entanglement at a fixed non-zero parameter count, we introduce Fixed Parameter Expansion (FPE): replace a neuron with multiple children and partition the parent's weights disjointly across them, so that each child inherits a non-overlapping subset of connections. On symbolic tasks, specifically Boolean code problems, clause-aligned FPE systematically reduces polysemanticity metrics and yields higher task accuracy. Notably, random splits of neuron weights approximate these gains, indicating that reduced collisions, not precise assignment, are a primary driver. Consistent with the superposition hypothesis, the benefits of FPE grow with increasing interference: when polysemantic load is high, accuracy improvements are the largest. Transferring these insights to real models (classifiers over CLIP embeddings and deeper multilayer networks) we find that widening networks while maintaining a constant non-zero parameter count consistently increases accuracy. These results identify an interpretability-grounded mechanism to leverage width against superposition, improving performance without increasing the number of non-zero parameters. Such a direction is well matched to modern accelerators, where memory movement of non-zero parameters, rather than raw compute, is the dominant bottleneck.

Sparse Expansion and Neuronal Disentanglement

We show how to improve the inference efficiency of an LLM by expanding it into a mixture of sparse experts, where each expert is a copy of the original weights, one-shot pruned for a specific cluster of input values. We call this approach $\textit{Sparse Expansion}$. We show that, for models such as Llama 2 70B, as we increase the number of sparse experts, Sparse Expansion outperforms all other one-shot sparsification approaches for the same inference FLOP budget per token, and that this gap grows as sparsity increases, leading to inference speedups. But why? To answer this, we provide strong evidence that the mixture of sparse experts is effectively $\textit{disentangling}$ the input-output relationship of every individual neuron across clusters of inputs. Specifically, sparse experts approximate the dense neuron output distribution with fewer weights by decomposing the distribution into a collection of simpler ones, each with a separate sparse dot product covering it. Interestingly, we show that the Wasserstein distance between a neuron's output distribution and a Gaussian distribution is an indicator of its entanglement level and contribution to the accuracy of the model. Every layer of an LLM has a fraction of highly entangled Wasserstein neurons, and model performance suffers more when these are sparsified as opposed to others.

Defending Adversarial Examples by Negative Correlation Ensemble

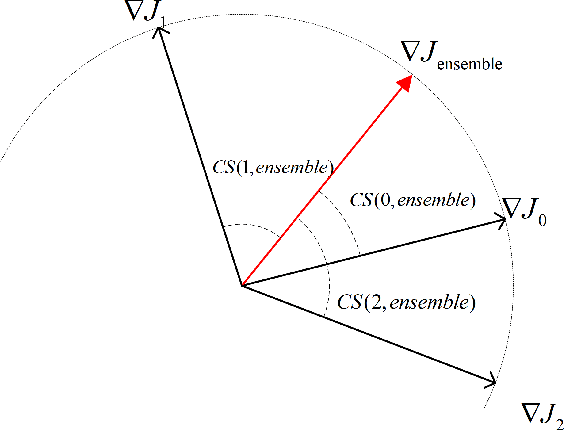
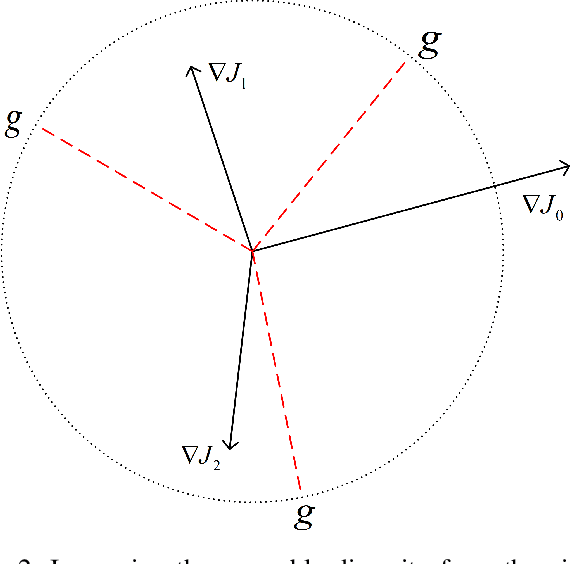
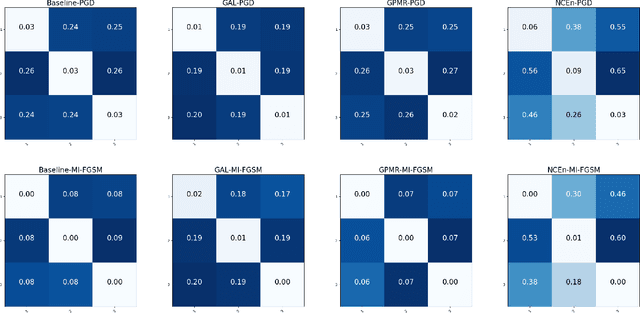
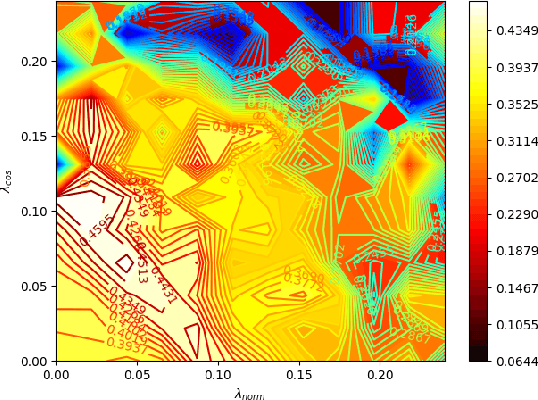
The security issues in DNNs, such as adversarial examples, have attracted much attention. Adversarial examples refer to the examples which are capable to induce the DNNs return completely predictions by introducing carefully designed perturbations. Obviously, adversarial examples bring great security risks to the development of deep learning. Recently, Some defense approaches against adversarial examples have been proposed, however, in our opinion, the performance of these approaches are still limited. In this paper, we propose a new ensemble defense approach named the Negative Correlation Ensemble (NCEn), which achieves compelling results by introducing gradient directions and gradient magnitudes of each member in the ensemble negatively correlated and at the same time, reducing the transferability of adversarial examples among them. Extensive experiments have been conducted, and the results demonstrate that NCEn can improve the adversarial robustness of ensembles effectively.