Approximate Cross-validation: Guarantees for Model Assessment and Selection

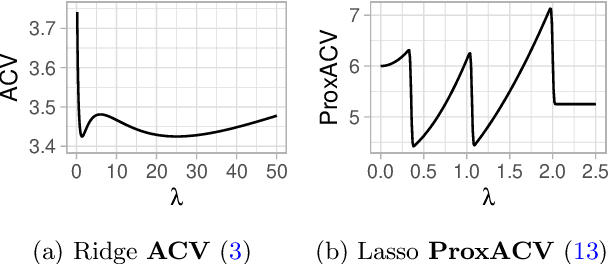
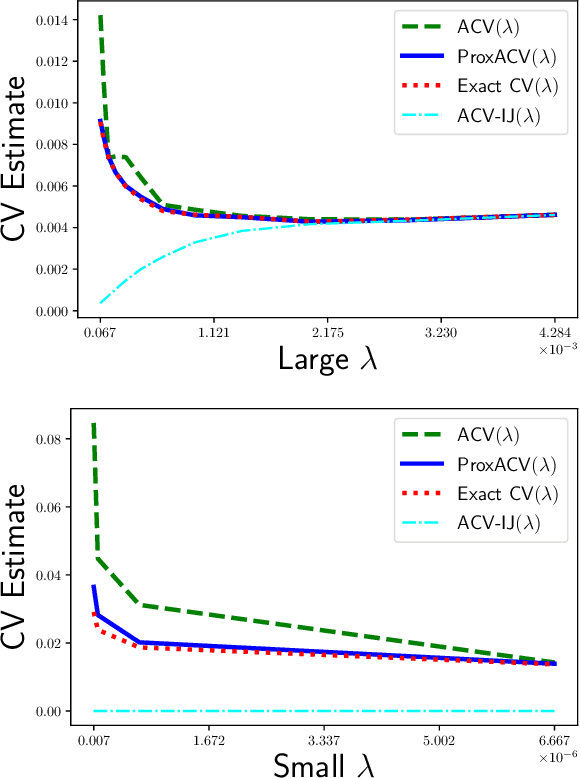
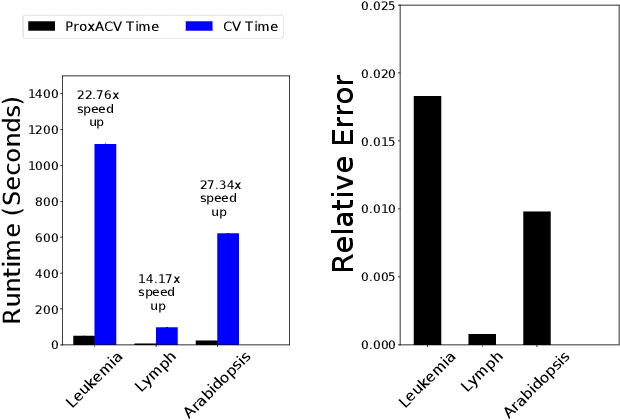
Cross-validation (CV) is a popular approach for assessing and selecting predictive models. However, when the number of folds is large, CV suffers from a need to repeatedly refit a learning procedure on a large number of training datasets. Recent work in empirical risk minimization (ERM) approximates the expensive refitting with a single Newton step warm-started from the full training set optimizer. While this can greatly reduce runtime, several open questions remain including whether these approximations lead to faithful model selection and whether they are suitable for non-smooth objectives. We address these questions with three main contributions: (i) we provide uniform non-asymptotic, deterministic model assessment guarantees for approximate CV; (ii) we show that (roughly) the same conditions also guarantee model selection performance comparable to CV; (iii) we provide a proximal Newton extension of the approximate CV framework for non-smooth prediction problems and develop improved assessment guarantees for problems such as l1-regularized ERM.

Importance Sampling via Local Sensitivity

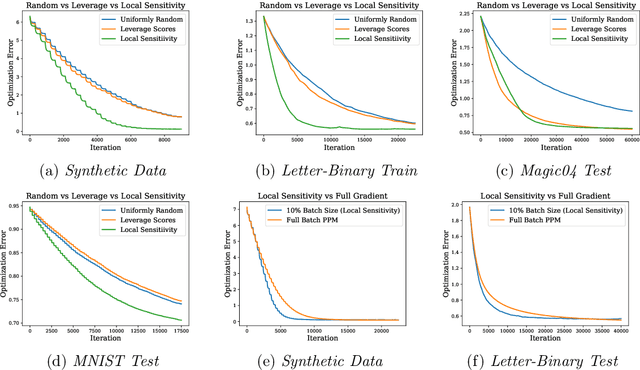
Given a loss function $F:\mathcal{X} \rightarrow \mathbb{R}^+$ that can be written as the sum of losses over a large set of inputs $a_1,\ldots, a_n$, it is often desirable to approximate $F$ by subsampling the input points. Strong theoretical guarantees require taking into account the importance of each point, measured by how much its individual loss contributes to $F(x)$. Maximizing this importance over all $x \in \mathcal{X}$ yields the \emph{sensitivity score} of $a_i$. Sampling with probabilities proportional to these scores gives strong provable guarantees, allowing one to approximately minimize of $F$ using just the subsampled points. Unfortunately, sensitivity sampling is difficult to apply since 1) it is unclear how to efficiently compute the sensitivity scores and 2) the sample size required is often too large to be useful. We propose overcoming both obstacles by introducing the \emph{local sensitivity}, which measures data point importance in a ball around some center $x_0$. We show that the local sensitivity can be efficiently estimated using the \emph{leverage scores} of a quadratic approximation to $F$, and that the sample size required to approximate $F$ around $x_0$ can be bounded. We propose employing local sensitivity sampling in an iterative optimization method and illustrate its usefulness by analyzing its convergence when $F$ is smooth and convex.

Debiasing Linear Prediction

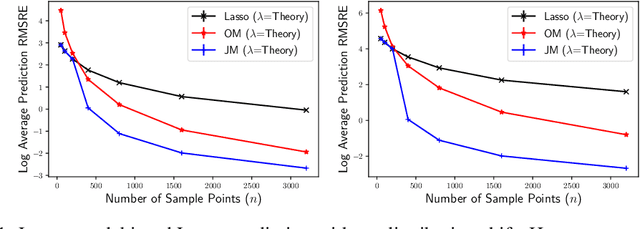
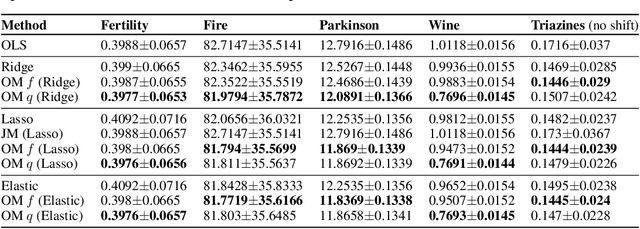
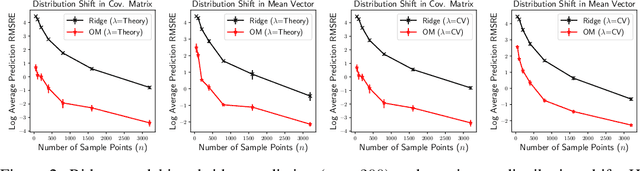
Standard methods in supervised learning separate training and prediction: the model is fit independently of any test points it may encounter. However, can knowledge of the next test point $\mathbf{x}_{\star}$ be exploited to improve prediction accuracy? We address this question in the context of linear prediction, showing how debiasing techniques can be used transductively to combat regularization bias. We first lower bound the $\mathbf{x}_{\star}$ prediction error of ridge regression and the Lasso, showing that they must incur significant bias in certain test directions. Then, building on techniques from semi-parametric inference, we provide non-asymptotic upper bounds on the $\mathbf{x}_{\star}$ prediction error of two transductive, debiased prediction rules. We conclude by showing the efficacy of our methods on both synthetic and real data, highlighting the improvements test-point-tailored debiasing can provide in settings with distribution shift.

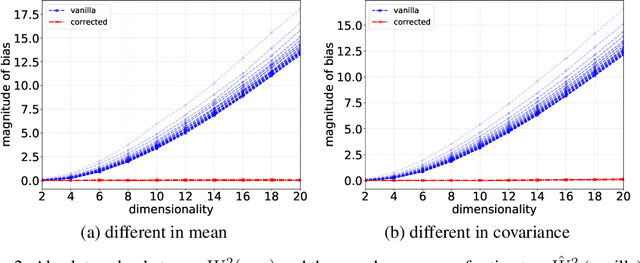
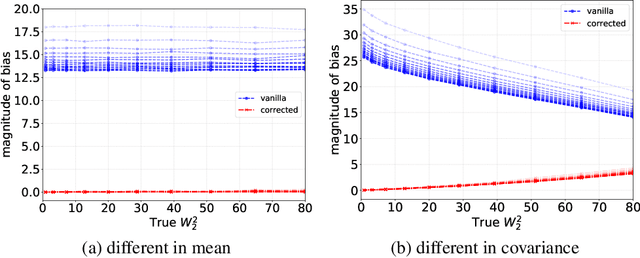
A Kernel Stein Test for Comparing Latent Variable Models

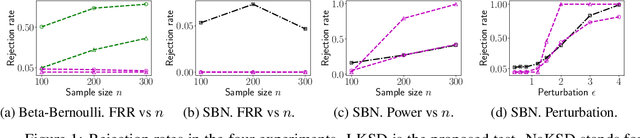
We propose a nonparametric, kernel-based test to assess the relative goodness of fit of latent variable models with intractable unnormalized densities. Our test generalises the kernel Stein discrepancy (KSD) tests of (Liu et al., 2016, Chwialkowski et al., 2016, Yang et al., 2018, Jitkrittum et al., 2018) which required exact access to unnormalized densities. Our new test relies on the simple idea of using an approximate observed-variable marginal in place of the exact, intractable one. As our main theoretical contribution, we prove that the new test, with a properly corrected threshold, has a well-controlled type-I error. In the case of models with low-dimensional latent structure and high-dimensional observations, our test significantly outperforms the relative maximum mean discrepancy test (Bounliphone et al., 2015) , which cannot exploit the latent structure.

Minimum Stein Discrepancy Estimators

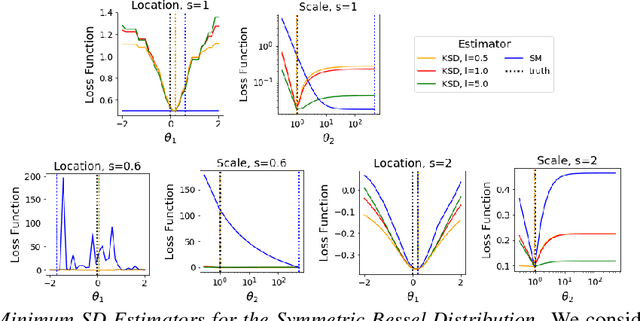
When maximum likelihood estimation is infeasible, one often turns to score matching, contrastive divergence, or minimum probability flow learning to obtain tractable parameter estimates. We provide a unifying perspective of these techniques as minimum Stein discrepancy estimators and use this lens to design new diffusion kernel Stein discrepancy (DKSD) and diffusion score matching (DSM) estimators with complementary strengths. We establish the consistency, asymptotic normality, and robustness of DKSD and DSM estimators, derive stochastic Riemannian gradient descent algorithms for their efficient optimization, and demonstrate their advantages over score matching in models with non-smooth densities or heavy tailed distributions.

Stochastic Runge-Kutta Accelerates Langevin Monte Carlo and Beyond

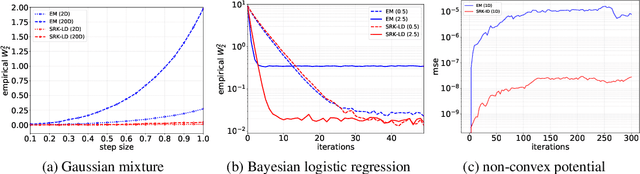
Sampling with Markov chain Monte Carlo methods typically amounts to discretizing some continuous-time dynamics with numerical integration. In this paper, we establish the convergence rate of sampling algorithms obtained by discretizing smooth It\^o diffusions exhibiting fast Wasserstein-$2$ contraction, based on local deviation properties of the integration scheme. In particular, we study a sampling algorithm constructed by discretizing the overdamped Langevin diffusion with the method of stochastic Runge-Kutta. For strongly convex potentials that are smooth up to a certain order, its iterates converge to the target distribution in $2$-Wasserstein distance in $\tilde{\mathcal{O}}(d\epsilon^{-2/3})$ iterations. This improves upon the best-known rate for strongly log-concave sampling based on the overdamped Langevin equation using only the gradient oracle without adjustment. In addition, we extend our analysis of stochastic Runge-Kutta methods to uniformly dissipative diffusions with possibly non-convex potentials and show they achieve better rates compared to the Euler-Maruyama scheme in terms of the dependence on tolerance $\epsilon$. Numerical studies show that these algorithms lead to better stability and lower asymptotic errors.

Stein Point Markov Chain Monte Carlo

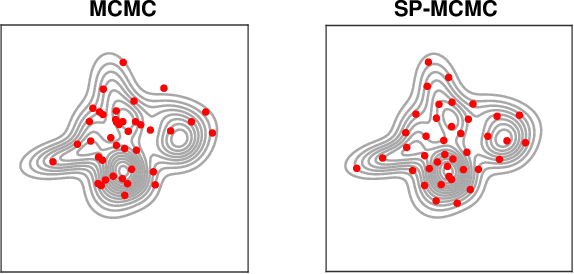
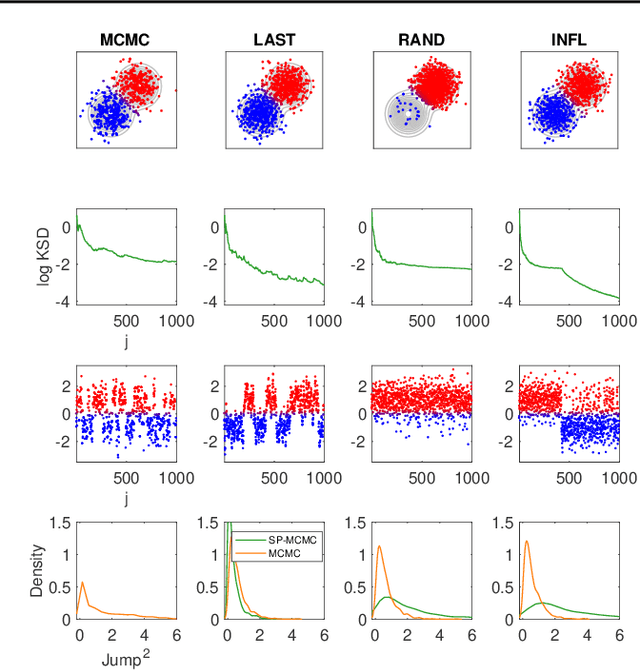
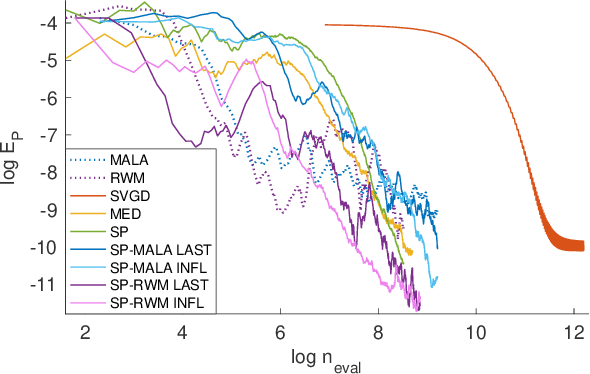
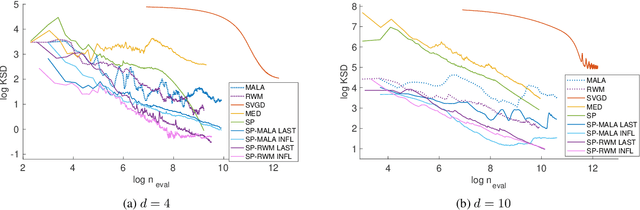
An important task in machine learning and statistics is the approximation of a probability measure by an empirical measure supported on a discrete point set. Stein Points are a class of algorithms for this task, which proceed by sequentially minimising a Stein discrepancy between the empirical measure and the target and, hence, require the solution of a non-convex optimisation problem to obtain each new point. This paper removes the need to solve this optimisation problem by, instead, selecting each new point based on a Markov chain sample path. This significantly reduces the computational cost of Stein Points and leads to a suite of algorithms that are straightforward to implement. The new algorithms are illustrated on a set of challenging Bayesian inference problems, and rigorous theoretical guarantees of consistency are established.

Model Compression with Generative Adversarial Networks

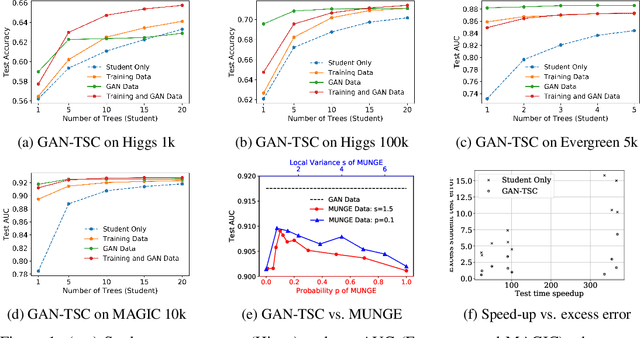
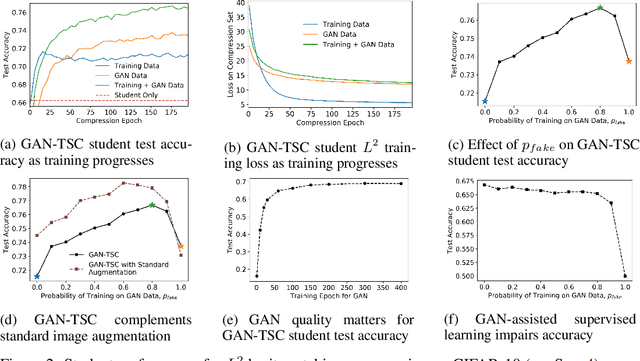
More accurate machine learning models often demand more computation and memory at test time, making them difficult to deploy on CPU- or memory-constrained devices. Model compression (also known as distillation) alleviates this burden by training a less expensive student model to mimic the expensive teacher model while maintaining most of the original accuracy. However, when fresh data is unavailable for the compression task, the teacher's training data is typically reused, leading to suboptimal compression. In this work, we propose to augment the compression dataset with synthetic data from a generative adversarial network (GAN) designed to approximate the training data distribution. Our GAN-assisted model compression (GAN-MC) significantly improves student accuracy for expensive models such as deep neural networks and large random forests on both image and tabular datasets. Building on these results, we propose a comprehensive metric---the Compression Score---to evaluate the quality of synthetic datasets based on their induced model compression performance. The Compression Score captures both data diversity and discriminability, and we illustrate its benefits over the popular Inception Score in the context of image classification.

Global Non-convex Optimization with Discretized Diffusions

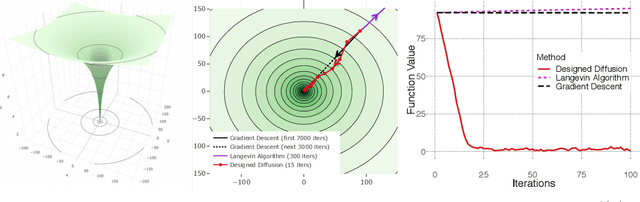
An Euler discretization of the Langevin diffusion is known to converge to the global minimizers of certain convex and non-convex optimization problems. We show that this property holds for any suitably smooth diffusion and that different diffusions are suitable for optimizing different classes of convex and non-convex functions. This allows us to design diffusions suitable for globally optimizing convex and non-convex functions not covered by the existing Langevin theory. Our non-asymptotic analysis delivers computable optimization and integration error bounds based on easily accessed properties of the objective and chosen diffusion. Central to our approach are new explicit Stein factor bounds on the solutions of Poisson equations. We complement these results with improved optimization guarantees for targets other than the standard Gibbs measure.

Random Feature Stein Discrepancies

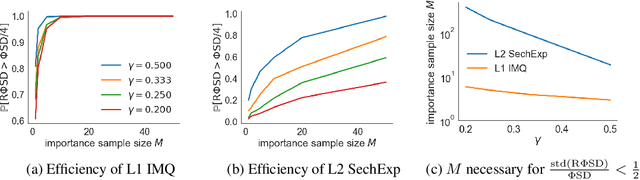
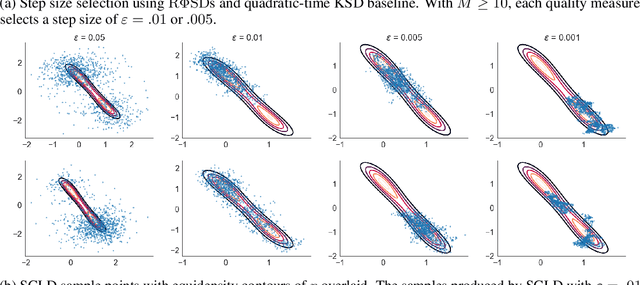
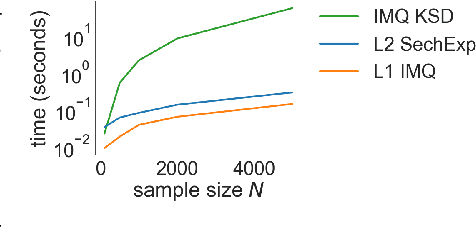
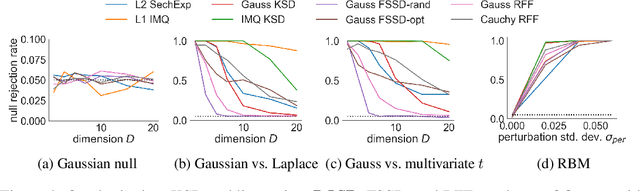
Computable Stein discrepancies have been deployed for a variety of applications, ranging from sampler selection in posterior inference to approximate Bayesian inference to goodness-of-fit testing. Existing convergence-determining Stein discrepancies admit strong theoretical guarantees but suffer from a computational cost that grows quadratically in the sample size. While linear-time Stein discrepancies have been proposed for goodness-of-fit testing, they exhibit avoidable degradations in testing power---even when power is explicitly optimized. To address these shortcomings, we introduce feature Stein discrepancies ($\Phi$SDs), a new family of quality measures that can be cheaply approximated using importance sampling. We show how to construct $\Phi$SDs that provably determine the convergence of a sample to its target and develop high-accuracy approximations---random $\Phi$SDs (R$\Phi$SDs)---which are computable in near-linear time. In our experiments with sampler selection for approximate posterior inference and goodness-of-fit testing, R$\Phi$SDs perform as well or better than quadratic-time KSDs while being orders of magnitude faster to compute.