Should I Stop or Should I Go: Early Stopping with Heterogeneous Populations

Randomized experiments often need to be stopped prematurely due to the treatment having an unintended harmful effect. Existing methods that determine when to stop an experiment early are typically applied to the data in aggregate and do not account for treatment effect heterogeneity. In this paper, we study the early stopping of experiments for harm on heterogeneous populations. We first establish that current methods often fail to stop experiments when the treatment harms a minority group of participants. We then use causal machine learning to develop CLASH, the first broadly-applicable method for heterogeneous early stopping. We demonstrate CLASH's performance on simulated and real data and show that it yields effective early stopping for both clinical trials and A/B tests.

Do Language Models Know When They're Hallucinating References?

Current state-of-the-art language models (LMs) are notorious for generating text with "hallucinations," a primary example being book and paper references that lack any solid basis in their training data. However, we find that many of these fabrications can be identified using the same LM, using only black-box queries without consulting any external resources. Consistency checks done with direct queries about whether the generated reference title is real (inspired by Kadavath et al. 2022, Lin et al. 2022, Manakul et al. 2023) are compared to consistency checks with indirect queries which ask for ancillary details such as the authors of the work. These consistency checks are found to be partially reliable indicators of whether or not the reference is a hallucination. In particular, we find that LMs in the GPT-series will hallucinate differing authors of hallucinated references when queried in independent sessions, while it will consistently identify authors of real references. This suggests that the hallucination may be more a result of generation techniques than the underlying representation.

Learning Rate Free Bayesian Inference in Constrained Domains

We introduce a suite of new particle-based algorithms for sampling on constrained domains which are entirely learning rate free. Our approach leverages coin betting ideas from convex optimisation, and the viewpoint of constrained sampling as a mirrored optimisation problem on the space of probability measures. Based on this viewpoint, we also introduce a unifying framework for several existing constrained sampling algorithms, including mirrored Langevin dynamics and mirrored Stein variational gradient descent. We demonstrate the performance of our algorithms on a range of numerical examples, including sampling from targets on the simplex, sampling with fairness constraints, and constrained sampling problems in post-selection inference. Our results indicate that our algorithms achieve competitive performance with existing constrained sampling methods, without the need to tune any hyperparameters.

Compress Then Test: Powerful Kernel Testing in Near-linear Time

Kernel two-sample testing provides a powerful framework for distinguishing any pair of distributions based on $n$ sample points. However, existing kernel tests either run in $n^2$ time or sacrifice undue power to improve runtime. To address these shortcomings, we introduce Compress Then Test (CTT), a new framework for high-powered kernel testing based on sample compression. CTT cheaply approximates an expensive test by compressing each $n$ point sample into a small but provably high-fidelity coreset. For standard kernels and subexponential distributions, CTT inherits the statistical behavior of a quadratic-time test -- recovering the same optimal detection boundary -- while running in near-linear time. We couple these advances with cheaper permutation testing, justified by new power analyses; improved time-vs.-quality guarantees for low-rank approximation; and a fast aggregation procedure for identifying especially discriminating kernels. In our experiments with real and simulated data, CTT and its extensions provide 20--200x speed-ups over state-of-the-art approximate MMD tests with no loss of power.

A Finite-Particle Convergence Rate for Stein Variational Gradient Descent

We provide a first finite-particle convergence rate for Stein variational gradient descent (SVGD). Specifically, whenever the target distribution is sub-Gaussian with a Lipschitz score, SVGD with n particles and an appropriate step size sequence drives the kernel Stein discrepancy to zero at an order 1/sqrt(log log n) rate. We suspect that the dependence on n can be improved, and we hope that our explicit, non-asymptotic proof strategy will serve as a template for future refinements.

Controlling Moments with Kernel Stein Discrepancies

Quantifying the deviation of a probability distribution is challenging when the target distribution is defined by a density with an intractable normalizing constant. The kernel Stein discrepancy (KSD) was proposed to address this problem and has been applied to various tasks including diagnosing approximate MCMC samplers and goodness-of-fit testing for unnormalized statistical models. This article investigates a convergence control property of the diffusion kernel Stein discrepancy (DKSD), an instance of the KSD proposed by Barp et al. (2019). We extend the result of Gorham and Mackey (2017), which showed that the KSD controls the bounded-Lipschitz metric, to functions of polynomial growth. Specifically, we prove that the DKSD controls the integral probability metric defined by a class of pseudo-Lipschitz functions, a polynomial generalization of Lipschitz functions. We also provide practical sufficient conditions on the reproducing kernel for the stated property to hold. In particular, we show that the DKSD detects non-convergence in moments with an appropriate kernel.

Budget-Constrained Bounds for Mini-Batch Estimation of Optimal Transport

Optimal Transport (OT) is a fundamental tool for comparing probability distributions, but its exact computation remains prohibitive for large datasets. In this work, we introduce novel families of upper and lower bounds for the OT problem constructed by aggregating solutions of mini-batch OT problems. The upper bound family contains traditional mini-batch averaging at one extreme and a tight bound found by optimal coupling of mini-batches at the other. In between these extremes, we propose various methods to construct bounds based on a fixed computational budget. Through various experiments, we explore the trade-off between computational budget and bound tightness and show the usefulness of these bounds in computer vision applications.

Targeted Separation and Convergence with Kernel Discrepancies

Maximum mean discrepancies (MMDs) like the kernel Stein discrepancy (KSD) have grown central to a wide range of applications, including hypothesis testing, sampler selection, distribution approximation, and variational inference. In each setting, these kernel-based discrepancy measures are required to (i) separate a target P from other probability measures or even (ii) control weak convergence to P. In this article we derive new sufficient and necessary conditions to ensure (i) and (ii). For MMDs on separable metric spaces, we characterize those kernels that separate Bochner embeddable measures and introduce simple conditions for separating all measures with unbounded kernels and for controlling convergence with bounded kernels. We use these results on $\mathbb{R}^d$ to substantially broaden the known conditions for KSD separation and convergence control and to develop the first KSDs known to exactly metrize weak convergence to P. Along the way, we highlight the implications of our results for hypothesis testing, measuring and improving sample quality, and sampling with Stein variational gradient descent.

Adaptive Bias Correction for Improved Subseasonal Forecasting

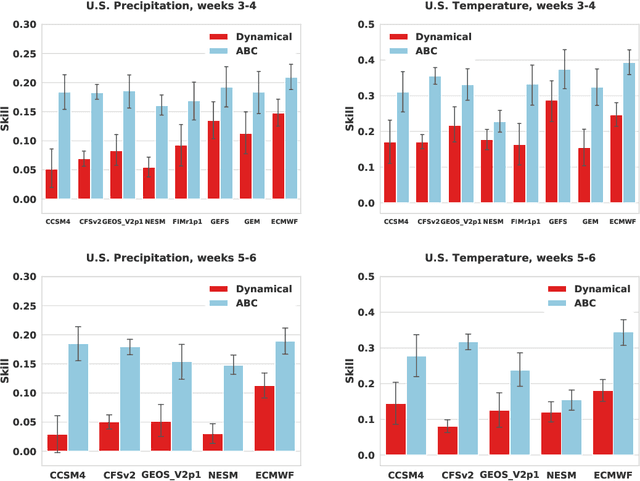
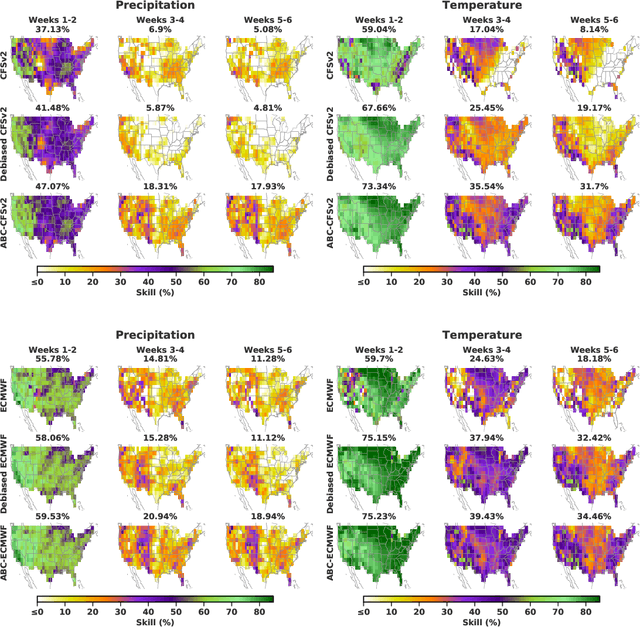
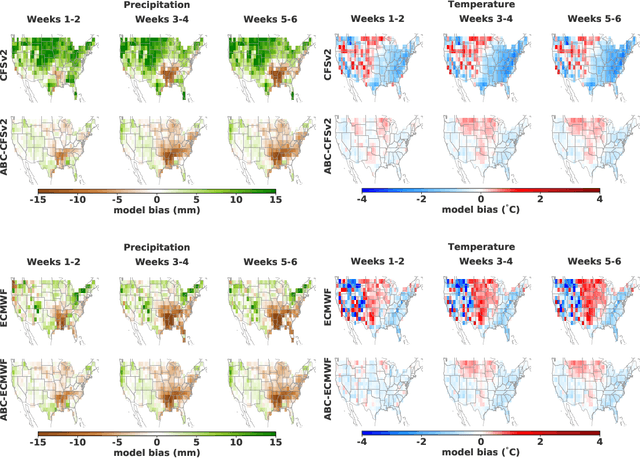
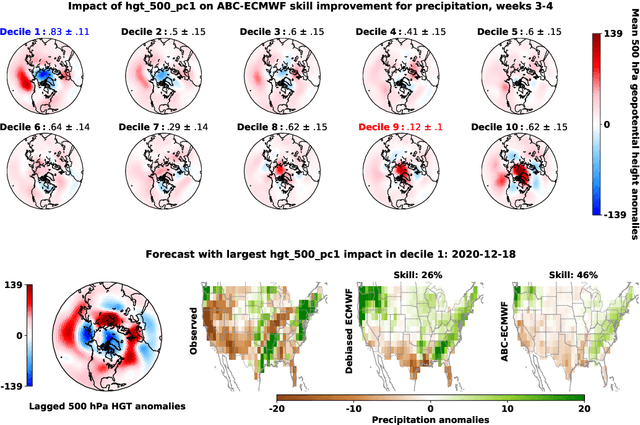
Subseasonal forecasting $\unicode{x2013}$ predicting temperature and precipitation 2 to 6 weeks $\unicode{x2013}$ ahead is critical for effective water allocation, wildfire management, and drought and flood mitigation. Recent international research efforts have advanced the subseasonal capabilities of operational dynamical models, yet temperature and precipitation prediction skills remains poor, partly due to stubborn errors in representing atmospheric dynamics and physics inside dynamical models. To counter these errors, we introduce an adaptive bias correction (ABC) method that combines state-of-the-art dynamical forecasts with observations using machine learning. When applied to the leading subseasonal model from the European Centre for Medium-Range Weather Forecasts (ECMWF), ABC improves temperature forecasting skill by 60-90% and precipitation forecasting skill by 40-69% in the contiguous U.S. We couple these performance improvements with a practical workflow, based on Cohort Shapley, for explaining ABC skill gains and identifying higher-skill windows of opportunity based on specific climate conditions.

Scalable Spike-and-Slab

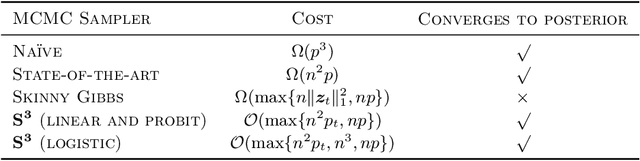
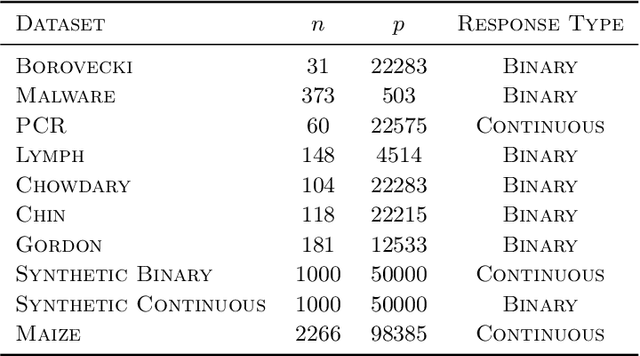
Spike-and-slab priors are commonly used for Bayesian variable selection, due to their interpretability and favorable statistical properties. However, existing samplers for spike-and-slab posteriors incur prohibitive computational costs when the number of variables is large. In this article, we propose Scalable Spike-and-Slab ($S^3$), a scalable Gibbs sampling implementation for high-dimensional Bayesian regression with the continuous spike-and-slab prior of George and McCulloch (1993). For a dataset with $n$ observations and $p$ covariates, $S^3$ has order $\max\{ n^2 p_t, np \}$ computational cost at iteration $t$ where $p_t$ never exceeds the number of covariates switching spike-and-slab states between iterations $t$ and $t-1$ of the Markov chain. This improves upon the order $n^2 p$ per-iteration cost of state-of-the-art implementations as, typically, $p_t$ is substantially smaller than $p$. We apply $S^3$ on synthetic and real-world datasets, demonstrating orders of magnitude speed-ups over existing exact samplers and significant gains in inferential quality over approximate samplers with comparable cost.