Scalable Monte Carlo for Bayesian Learning

This book aims to provide a graduate-level introduction to advanced topics in Markov chain Monte Carlo (MCMC) algorithms, as applied broadly in the Bayesian computational context. Most, if not all of these topics (stochastic gradient MCMC, non-reversible MCMC, continuous time MCMC, and new techniques for convergence assessment) have emerged as recently as the last decade, and have driven substantial recent practical and theoretical advances in the field. A particular focus is on methods that are scalable with respect to either the amount of data, or the data dimension, motivated by the emerging high-priority application areas in machine learning and AI.

Learning-Rate-Free Stochastic Optimization over Riemannian Manifolds

In recent years, interest in gradient-based optimization over Riemannian manifolds has surged. However, a significant challenge lies in the reliance on hyperparameters, especially the learning rate, which requires meticulous tuning by practitioners to ensure convergence at a suitable rate. In this work, we introduce innovative learning-rate-free algorithms for stochastic optimization over Riemannian manifolds, eliminating the need for hand-tuning and providing a more robust and user-friendly approach. We establish high probability convergence guarantees that are optimal, up to logarithmic factors, compared to the best-known optimally tuned rate in the deterministic setting. Our approach is validated through numerical experiments, demonstrating competitive performance against learning-rate-dependent algorithms.

Markovian Flow Matching: Accelerating MCMC with Continuous Normalizing Flows

Continuous normalizing flows (CNFs) learn the probability path between a reference and a target density by modeling the vector field generating said path using neural networks. Recently, Lipman et al. (2022) introduced a simple and inexpensive method for training CNFs in generative modeling, termed flow matching (FM). In this paper, we re-purpose this method for probabilistic inference by incorporating Markovian sampling methods in evaluating the FM objective and using the learned probability path to improve Monte Carlo sampling. We propose a sequential method, which uses samples from a Markov chain to fix the probability path defining the FM objective. We augment this scheme with an adaptive tempering mechanism that allows the discovery of multiple modes in the target. Under mild assumptions, we establish convergence to a local optimum of the FM objective, discuss improvements in the convergence rate, and illustrate our methods on synthetic and real-world examples.

Position Paper: Bayesian Deep Learning in the Age of Large-Scale AI

In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. This paper posits that BDL can elevate the capabilities of deep learning. It revisits the strengths of BDL, acknowledges existing challenges, and highlights some exciting research avenues aimed at addressing these obstacles. Looking ahead, the discussion focuses on possible ways to combine large-scale foundation models with BDL to unlock their full potential.

CoinEM: Tuning-Free Particle-Based Variational Inference for Latent Variable Models

We introduce two new particle-based algorithms for learning latent variable models via marginal maximum likelihood estimation, including one which is entirely tuning-free. Our methods are based on the perspective of marginal maximum likelihood estimation as an optimization problem: namely, as the minimization of a free energy functional. One way to solve this problem is to consider the discretization of a gradient flow associated with the free energy. We study one such approach, which resembles an extension of the popular Stein variational gradient descent algorithm. In particular, we establish a descent lemma for this algorithm, which guarantees that the free energy decreases at each iteration. This method, and any other obtained as the discretization of the gradient flow, will necessarily depend on a learning rate which must be carefully tuned by the practitioner in order to ensure convergence at a suitable rate. With this in mind, we also propose another algorithm for optimizing the free energy which is entirely learning rate free, based on coin betting techniques from convex optimization. We validate the performance of our algorithms across a broad range of numerical experiments, including several high-dimensional settings. Our results are competitive with existing particle-based methods, without the need for any hyperparameter tuning.

Learning Rate Free Bayesian Inference in Constrained Domains

We introduce a suite of new particle-based algorithms for sampling on constrained domains which are entirely learning rate free. Our approach leverages coin betting ideas from convex optimisation, and the viewpoint of constrained sampling as a mirrored optimisation problem on the space of probability measures. Based on this viewpoint, we also introduce a unifying framework for several existing constrained sampling algorithms, including mirrored Langevin dynamics and mirrored Stein variational gradient descent. We demonstrate the performance of our algorithms on a range of numerical examples, including sampling from targets on the simplex, sampling with fairness constraints, and constrained sampling problems in post-selection inference. Our results indicate that our algorithms achieve competitive performance with existing constrained sampling methods, without the need to tune any hyperparameters.

Coin Sampling: Gradient-Based Bayesian Inference without Learning Rates

In recent years, particle-based variational inference (ParVI) methods such as Stein variational gradient descent (SVGD) have grown in popularity as scalable methods for Bayesian inference. Unfortunately, the properties of such methods invariably depend on hyperparameters such as the learning rate, which must be carefully tuned by the practitioner in order to ensure convergence to the target measure at a suitable rate. In this paper, we introduce a suite of new particle-based methods for scalable Bayesian inference based on coin betting, which are entirely learning-rate free. We illustrate the performance of our approach on a range of numerical examples, including several high-dimensional models and datasets, demonstrating comparable performance to other ParVI algorithms.

Preferential Subsampling for Stochastic Gradient Langevin Dynamics

Stochastic gradient MCMC (SGMCMC) offers a scalable alternative to traditional MCMC, by constructing an unbiased estimate of the gradient of the log-posterior with a small, uniformly-weighted subsample of the data. While efficient to compute, the resulting gradient estimator may exhibit a high variance and impact sampler performance. The problem of variance control has been traditionally addressed by constructing a better stochastic gradient estimator, often using control variates. We propose to use a discrete, non-uniform probability distribution to preferentially subsample data points that have a greater impact on the stochastic gradient. In addition, we present a method of adaptively adjusting the subsample size at each iteration of the algorithm, so that we increase the subsample size in areas of the sample space where the gradient is harder to estimate. We demonstrate that such an approach can maintain the same level of accuracy while substantially reducing the average subsample size that is used.

SwISS: A Scalable Markov chain Monte Carlo Divide-and-Conquer Strategy

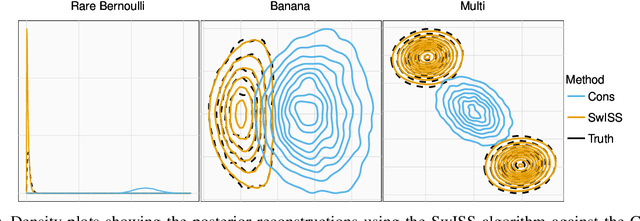
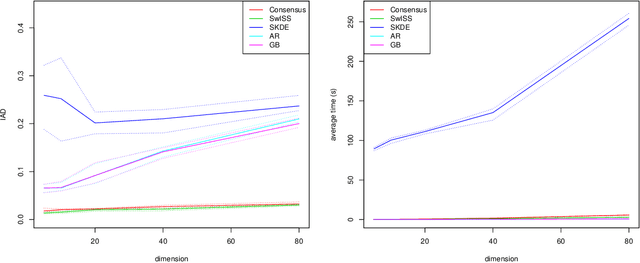
Divide-and-conquer strategies for Monte Carlo algorithms are an increasingly popular approach to making Bayesian inference scalable to large data sets. In its simplest form, the data are partitioned across multiple computing cores and a separate Markov chain Monte Carlo algorithm on each core targets the associated partial posterior distribution, which we refer to as a sub-posterior, that is the posterior given only the data from the segment of the partition associated with that core. Divide-and-conquer techniques reduce computational, memory and disk bottle-necks, but make it difficult to recombine the sub-posterior samples. We propose SwISS: Sub-posteriors with Inflation, Scaling and Shifting; a new approach for recombining the sub-posterior samples which is simple to apply, scales to high-dimensional parameter spaces and accurately approximates the original posterior distribution through affine transformations of the sub-posterior samples. We prove that our transformation is asymptotically optimal across a natural set of affine transformations and illustrate the efficacy of SwISS against competing algorithms on synthetic and real-world data sets.

Gaussian Processes on Hypergraphs

We derive a Matern Gaussian process (GP) on the vertices of a hypergraph. This enables estimation of regression models of observed or latent values associated with the vertices, in which the correlation and uncertainty estimates are informed by the hypergraph structure. We further present a framework for embedding the vertices of a hypergraph into a latent space using the hypergraph GP. Finally, we provide a scheme for identifying a small number of representative inducing vertices that enables scalable inference through sparse GPs. We demonstrate the utility of our framework on three challenging real-world problems that concern multi-class classification for the political party affiliation of legislators on the basis of voting behaviour, probabilistic matrix factorisation of movie reviews, and embedding a hypergraph of animals into a low-dimensional latent space.