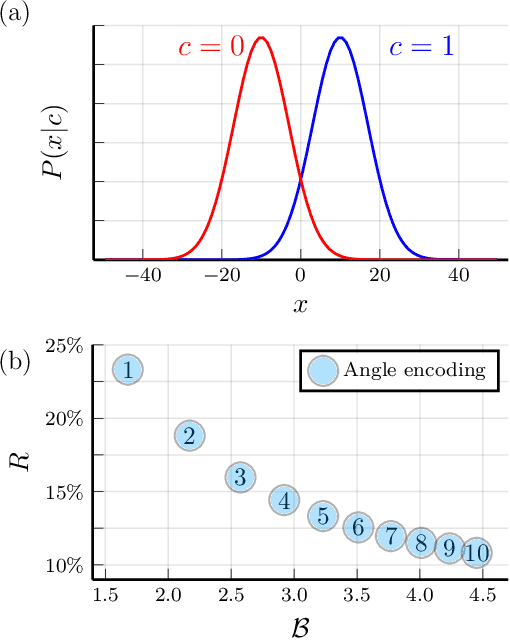
Few measurement shots challenge generalization in learning to classify entanglement

The ability to extract general laws from a few known examples depends on the complexity of the problem and on the amount of training data. In the quantum setting, the learner's generalization performance is further challenged by the destructive nature of quantum measurements that, together with the no-cloning theorem, limits the amount of information that can be extracted from each training sample. In this paper we focus on hybrid quantum learning techniques where classical machine-learning methods are paired with quantum algorithms and show that, in some settings, the uncertainty coming from a few measurement shots can be the dominant source of errors. We identify an instance of this possibly general issue by focusing on the classification of maximally entangled vs. separable states, showing that this toy problem becomes challenging for learners unaware of entanglement theory. Finally, we introduce an estimator based on classical shadows that performs better in the big data, few copy regime. Our results show that the naive application of classical machine-learning methods to the quantum setting is problematic, and that a better theoretical foundation of quantum learning is required.

Generalization in Quantum Machine Learning: a Quantum Information Perspective

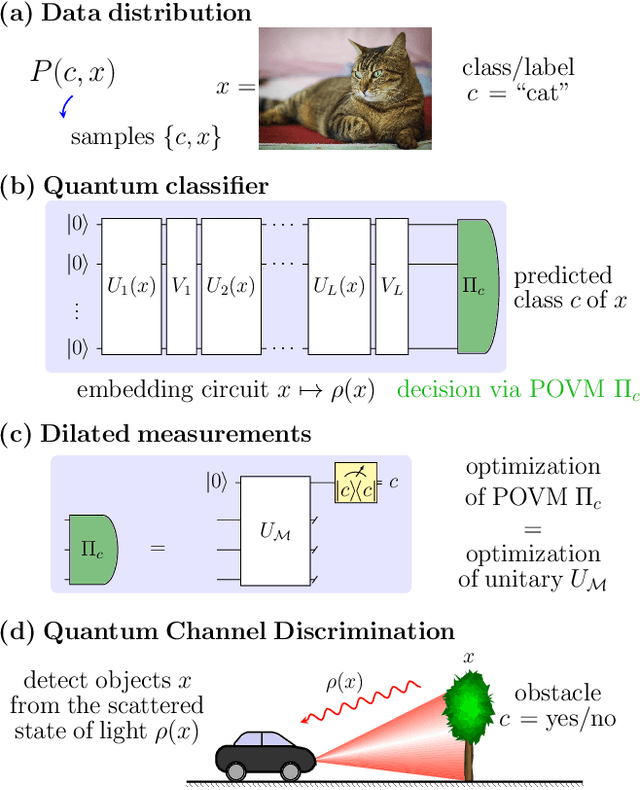
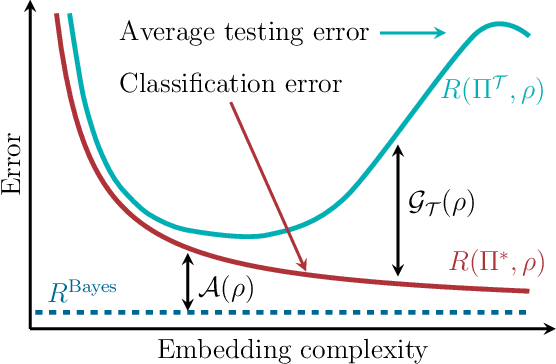
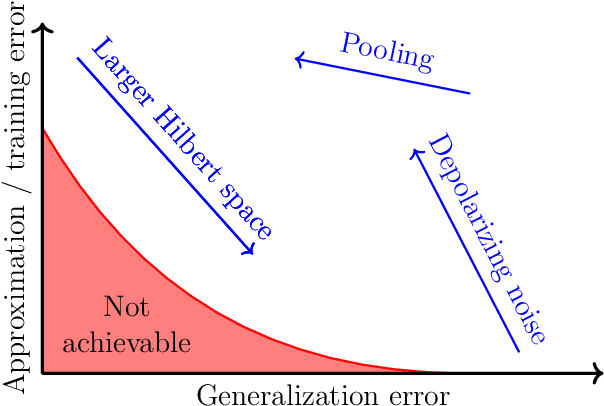
We study the machine learning problem of generalization when quantum operations are used to classify either classical data or quantum channels, where in both cases the task is to learn from data how to assign a certain class $c$ to inputs $x$ via measurements on a quantum state $\rho(x)$. A trained quantum model generalizes when it is able to predict the correct class for previously unseen data. We show that the accuracy and generalization capability of quantum classifiers depend on the (R\'enyi) mutual informations $I(C{:}Q)$ and $I_2(X{:}Q)$ between the quantum embedding $Q$ and the classical input space $X$ or class space $C$. Based on the above characterization, we then show how different properties of $Q$ affect classification accuracy and generalization, such as the dimension of the Hilbert space, the amount of noise, and the amount of neglected information via, e.g., pooling layers. Moreover, we introduce a quantum version of the Information Bottleneck principle that allows us to explore the various tradeoffs between accuracy and generalization.