A Model Zoo of Vision Transformers

The availability of large, structured populations of neural networks - called 'model zoos' - has led to the development of a multitude of downstream tasks ranging from model analysis, to representation learning on model weights or generative modeling of neural network parameters. However, existing model zoos are limited in size and architecture and neglect the transformer, which is among the currently most successful neural network architectures. We address this gap by introducing the first model zoo of vision transformers (ViT). To better represent recent training approaches, we develop a new blueprint for model zoo generation that encompasses both pre-training and fine-tuning steps, and publish 250 unique models. They are carefully generated with a large span of generating factors, and their diversity is validated using a thorough choice of weight-space and behavioral metrics. To further motivate the utility of our proposed dataset, we suggest multiple possible applications grounded in both extensive exploratory experiments and a number of examples from the existing literature. By extending previous lines of similar work, our model zoo allows researchers to push their model population-based methods from the small model regime to state-of-the-art architectures. We make our model zoo available at github.com/ModelZoos/ViTModelZoo.

Structure Is Not Enough: Leveraging Behavior for Neural Network Weight Reconstruction

The weights of neural networks (NNs) have recently gained prominence as a new data modality in machine learning, with applications ranging from accuracy and hyperparameter prediction to representation learning or weight generation. One approach to leverage NN weights involves training autoencoders (AEs), using contrastive and reconstruction losses. This allows such models to be applied to a wide variety of downstream tasks, and they demonstrate strong predictive performance and low reconstruction error. However, despite the low reconstruction error, these AEs reconstruct NN models with deteriorated performance compared to the original ones, limiting their usability with regard to model weight generation. In this paper, we identify a limitation of weight-space AEs, specifically highlighting that a structural loss, that uses the Euclidean distance between original and reconstructed weights, fails to capture some features critical for reconstructing high-performing models. We analyze the addition of a behavioral loss for training AEs in weight space, where we compare the output of the reconstructed model with that of the original one, given some common input. We show a strong synergy between structural and behavioral signals, leading to increased performance in all downstream tasks evaluated, in particular NN weights reconstruction and generation.

Distribution inference risks: Identifying and mitigating sources of leakage

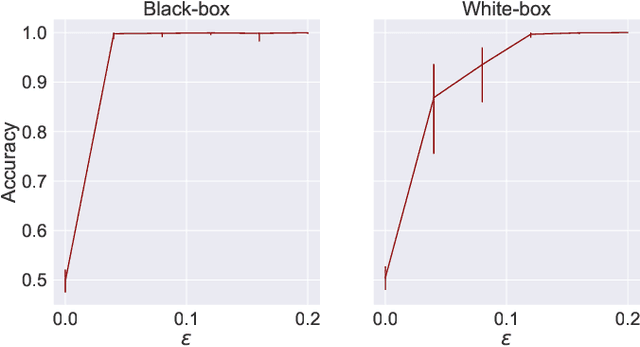
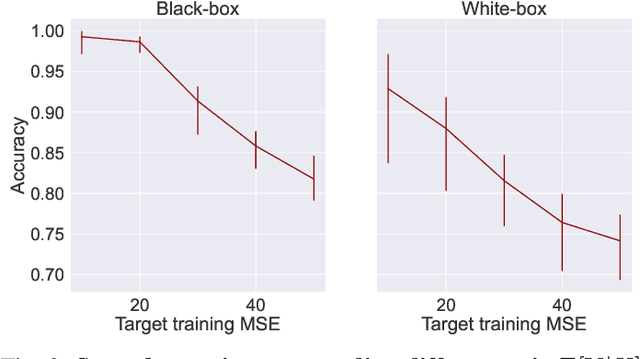
A large body of work shows that machine learning (ML) models can leak sensitive or confidential information about their training data. Recently, leakage due to distribution inference (or property inference) attacks is gaining attention. In this attack, the goal of an adversary is to infer distributional information about the training data. So far, research on distribution inference has focused on demonstrating successful attacks, with little attention given to identifying the potential causes of the leakage and to proposing mitigations. To bridge this gap, as our main contribution, we theoretically and empirically analyze the sources of information leakage that allows an adversary to perpetrate distribution inference attacks. We identify three sources of leakage: (1) memorizing specific information about the $\mathbb{E}[Y|X]$ (expected label given the feature values) of interest to the adversary, (2) wrong inductive bias of the model, and (3) finiteness of the training data. Next, based on our analysis, we propose principled mitigation techniques against distribution inference attacks. Specifically, we demonstrate that causal learning techniques are more resilient to a particular type of distribution inference risk termed distributional membership inference than associative learning methods. And lastly, we present a formalization of distribution inference that allows for reasoning about more general adversaries than was previously possible.