Discussing the Spectra of Physics-Enhanced Machine Learning via a Survey on Structural Mechanics Applications

The intersection of physics and machine learning has given rise to a paradigm that we refer to here as physics-enhanced machine learning (PEML), aiming to improve the capabilities and reduce the individual shortcomings of data- or physics-only methods. In this paper, the spectrum of physics-enhanced machine learning methods, expressed across the defining axes of physics and data, is discussed by engaging in a comprehensive exploration of its characteristics, usage, and motivations. In doing so, this paper offers a survey of recent applications and developments of PEML techniques, revealing the potency of PEML in addressing complex challenges. We further demonstrate application of select such schemes on the simple working example of a single-degree-of-freedom Duffing oscillator, which allows to highlight the individual characteristics and motivations of different `genres' of PEML approaches. To promote collaboration and transparency, and to provide practical examples for the reader, the code of these working examples is provided alongside this paper. As a foundational contribution, this paper underscores the significance of PEML in pushing the boundaries of scientific and engineering research, underpinned by the synergy of physical insights and machine learning capabilities.

Neural Extended Kalman Filters for Learning and Predicting Dynamics of Structural Systems

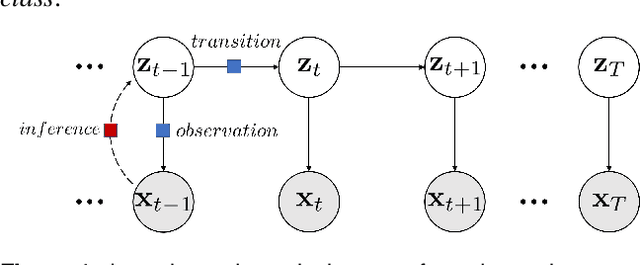
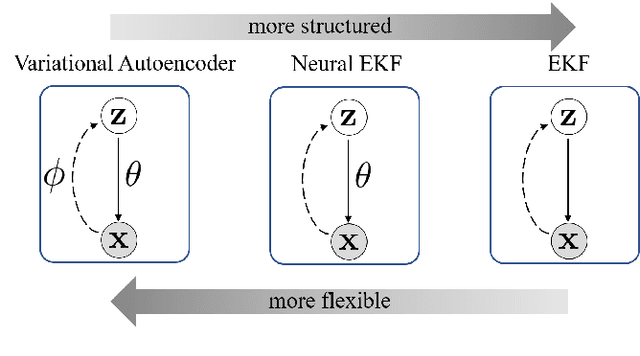
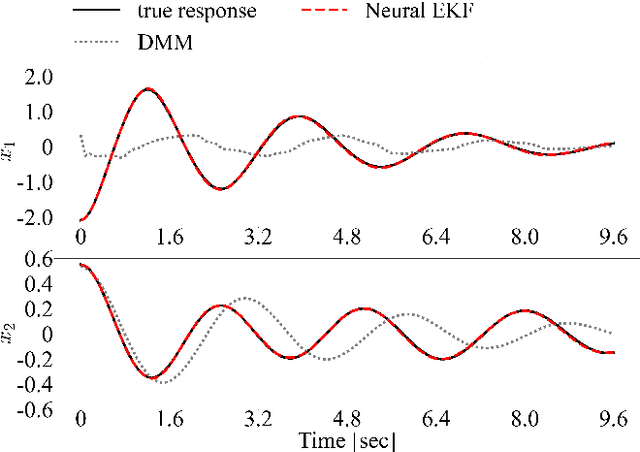
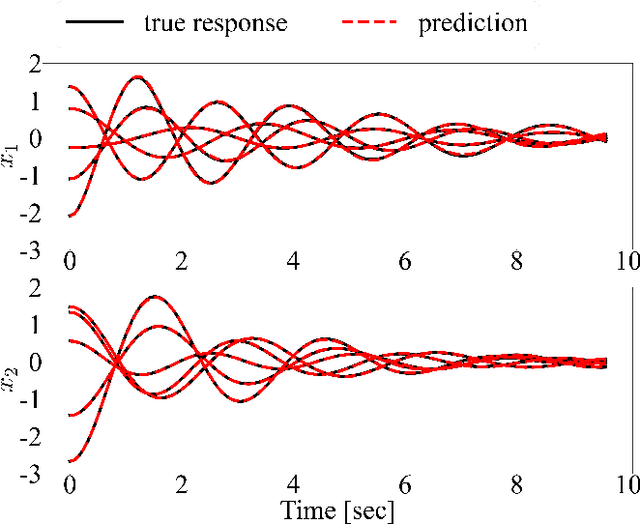
Accurate structural response prediction forms a main driver for structural health monitoring and control applications. This often requires the proposed model to adequately capture the underlying dynamics of complex structural systems. In this work, we utilize a learnable Extended Kalman Filter (EKF), named the Neural Extended Kalman Filter (Neural EKF) throughout this paper, for learning the latent evolution dynamics of complex physical systems. The Neural EKF is a generalized version of the conventional EKF, where the modeling of process dynamics and sensory observations can be parameterized by neural networks, therefore learned by end-to-end training. The method is implemented under the variational inference framework with the EKF conducting inference from sensing measurements. Typically, conventional variational inference models are parameterized by neural networks independent of the latent dynamics models. This characteristic makes the inference and reconstruction accuracy weakly based on the dynamics models and renders the associated training inadequate. We here show how the structure imposed by the Neural EKF is beneficial to the learning process. We demonstrate the efficacy of the framework on both simulated and real-world monitoring datasets, with the results indicating significant predictive capabilities of the proposed scheme.

Neural Modal ODEs: Integrating Physics-based Modeling with Neural ODEs for Modeling High Dimensional Monitored Structures

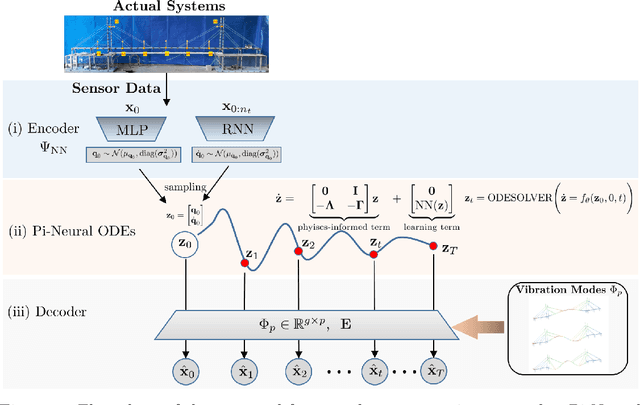
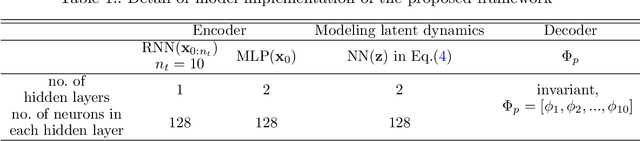
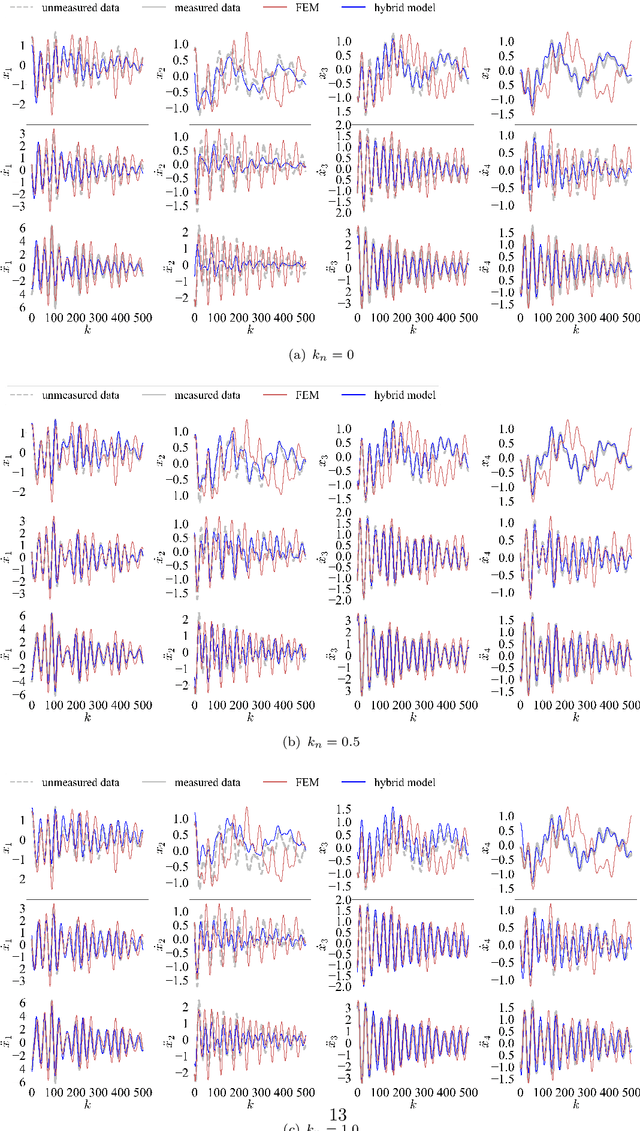
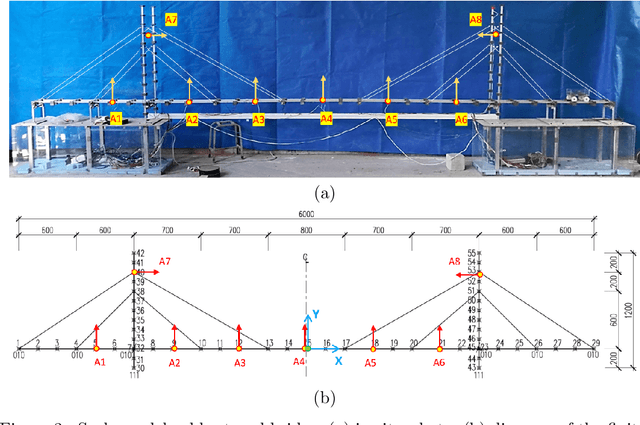
The order/dimension of models derived on the basis of data is commonly restricted by the number of observations, or in the context of monitored systems, sensing nodes. This is particularly true for structural systems (e.g. civil or mechanical structures), which are typically high-dimensional in nature. In the scope of physics-informed machine learning, this paper proposes a framework - termed Neural Modal ODEs - to integrate physics-based modeling with deep learning (particularly, Neural Ordinary Differential Equations -- Neural ODEs) for modeling the dynamics of monitored and high-dimensional engineered systems. In this initiating exploration, we restrict ourselves to linear or mildly nonlinear systems. We propose an architecture that couples a dynamic version of variational autoencoders with physics-informed Neural ODEs (Pi-Neural ODEs). An encoder, as a part of the autoencoder, learns the abstract mappings from the first few items of observational data to the initial values of the latent variables, which drive the learning of embedded dynamics via physics-informed Neural ODEs, imposing a \textit{modal model} structure to that latent space. The decoder of the proposed model adopts the eigenmodes derived from an eigen-analysis applied to the linearized portion of a physics-based model: a process implicitly carrying the spatial relationship between degrees-of-freedom (DOFs). The framework is validated on a numerical example, and an experimental dataset of a scaled cable-stayed bridge, where the learned hybrid model is shown to outperform a purely physics-based approach to modeling. We further show the functionality of the proposed scheme within the context of virtual sensing, i.e., the recovery of generalized response quantities in unmeasured DOFs from spatially sparse data.

Physics-guided Deep Markov Models for Learning Nonlinear Dynamical Systems with Uncertainty

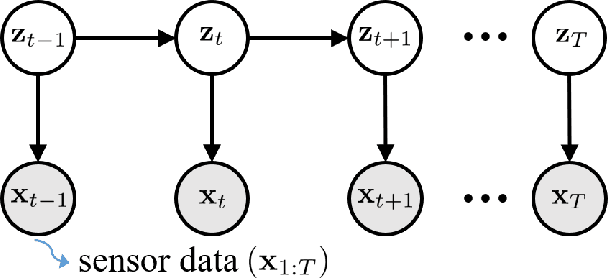
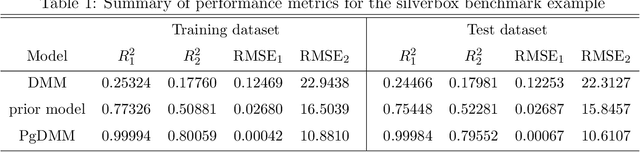
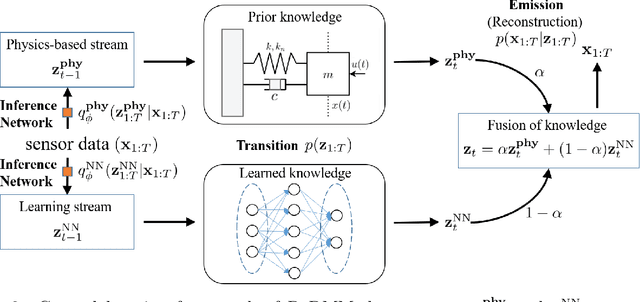
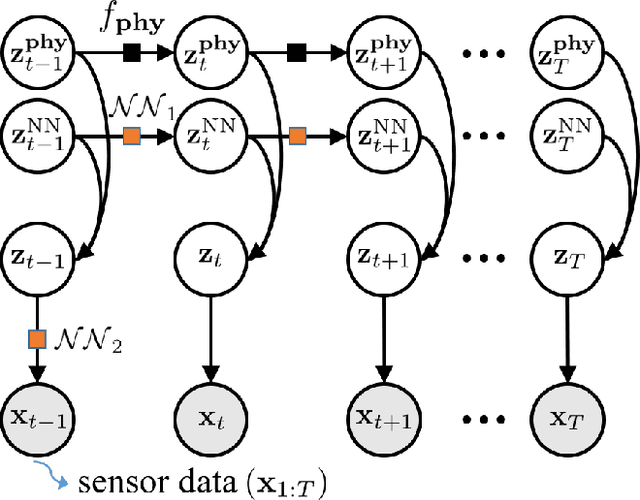
In this paper, we propose a probabilistic physics-guided framework, termed Physics-guided Deep Markov Model (PgDMM). The framework is especially targeted to the inference of the characteristics and latent structure of nonlinear dynamical systems from measurement data, where it is typically intractable to perform exact inference of latent variables. A recently surfaced option pertains to leveraging variational inference to perform approximate inference. In such a scheme, transition and emission functions of the system are parameterized via feed-forward neural networks (deep generative models). However, due to the generalized and highly versatile formulation of neural network functions, the learned latent space is often prone to lack physical interpretation and structured representation. To address this, we bridge physics-based state space models with Deep Markov Models, thus delivering a hybrid modeling framework for unsupervised learning and identification for nonlinear dynamical systems. Specifically, the transition process can be modeled as a physics-based model enhanced with an additive neural network component, which aims to learn the discrepancy between the physics-based model and the actual dynamical system being monitored. The proposed framework takes advantage of the expressive power of deep learning, while retaining the driving physics of the dynamical system by imposing physics-driven restrictions on the side of the latent space. We demonstrate the benefits of such a fusion in terms of achieving improved performance on illustrative simulation examples and experimental case studies of nonlinear systems. Our results indicate that the physics-based models involved in the employed transition and emission functions essentially enforce a more structured and physically interpretable latent space, which is essential to generalization and prediction capabilities.