Kent Lyons
Learning to Represent Individual Differences for Choice Decision Making
Mar 27, 2025Abstract:Human decision making can be challenging to predict because decisions are affected by a number of complex factors. Adding to this complexity, decision-making processes can differ considerably between individuals, and methods aimed at predicting human decisions need to take individual differences into account. Behavioral science offers methods by which to measure individual differences (e.g., questionnaires, behavioral models), but these are often narrowed down to low dimensions and not tailored to specific prediction tasks. This paper investigates the use of representation learning to measure individual differences from behavioral experiment data. Representation learning offers a flexible approach to create individual embeddings from data that are both structured (e.g., demographic information) and unstructured (e.g., free text), where the flexibility provides more options for individual difference measures for personalization, e.g., free text responses may allow for open-ended questions that are less privacy-sensitive. In the current paper we use representation learning to characterize individual differences in human performance on an economic decision-making task. We demonstrate that models using representation learning to capture individual differences consistently improve decision predictions over models without representation learning, and even outperform well-known theory-based behavioral models used in these environments. Our results propose that representation learning offers a useful and flexible tool to capture individual differences.
Accelerating Understanding of Scientific Experiments with End to End Symbolic Regression
Dec 07, 2021
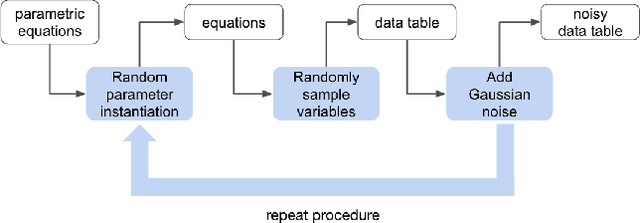
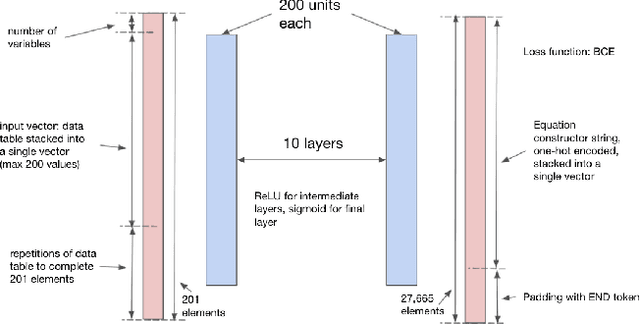
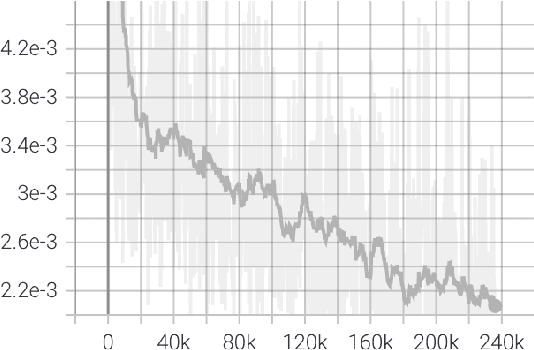
Abstract:We consider the problem of learning free-form symbolic expressions from raw data, such as that produced by an experiment in any scientific domain. Accurate and interpretable models of scientific phenomena are the cornerstone of scientific research. Simple yet interpretable models, such as linear or logistic regression and decision trees often lack predictive accuracy. Alternatively, accurate blackbox models such as deep neural networks provide high predictive accuracy, but do not readily admit human understanding in a way that would enrich the scientific theory of the phenomenon. Many great breakthroughs in science revolve around the development of parsimonious equational models with high predictive accuracy, such as Newton's laws, universal gravitation, and Maxwell's equations. Previous work on automating the search of equational models from data combine domain-specific heuristics as well as computationally expensive techniques, such as genetic programming and Monte-Carlo search. We develop a deep neural network (MACSYMA) to address the symbolic regression problem as an end-to-end supervised learning problem. MACSYMA can generate symbolic expressions that describe a dataset. The computational complexity of the task is reduced to the feedforward computation of a neural network. We train our neural network on a synthetic dataset consisting of data tables of varying length and varying levels of noise, for which the neural network must learn to produce the correct symbolic expression token by token. Finally, we validate our technique by running on a public dataset from behavioral science.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge