Complete Dictionary Recovery over the Sphere II: Recovery by Riemannian Trust-region Method

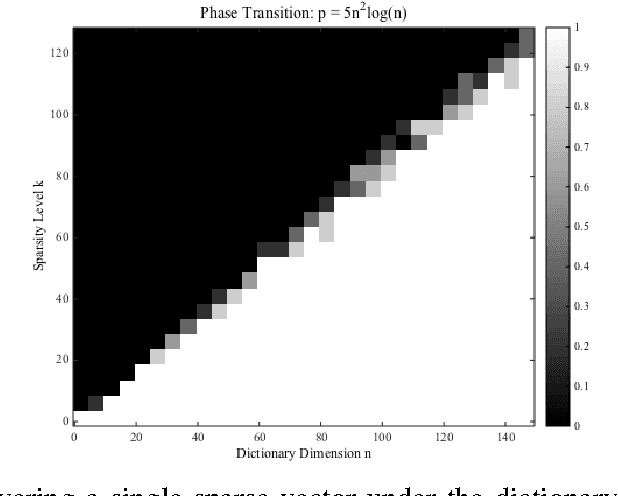
We consider the problem of recovering a complete (i.e., square and invertible) matrix $\mathbf A_0$, from $\mathbf Y \in \mathbb{R}^{n \times p}$ with $\mathbf Y = \mathbf A_0 \mathbf X_0$, provided $\mathbf X_0$ is sufficiently sparse. This recovery problem is central to theoretical understanding of dictionary learning, which seeks a sparse representation for a collection of input signals and finds numerous applications in modern signal processing and machine learning. We give the first efficient algorithm that provably recovers $\mathbf A_0$ when $\mathbf X_0$ has $O(n)$ nonzeros per column, under suitable probability model for $\mathbf X_0$. Our algorithmic pipeline centers around solving a certain nonconvex optimization problem with a spherical constraint, and hence is naturally phrased in the language of manifold optimization. In a companion paper (arXiv:1511.03607), we have showed that with high probability our nonconvex formulation has no "spurious" local minimizers and around any saddle point the objective function has a negative directional curvature. In this paper, we take advantage of the particular geometric structure, and describe a Riemannian trust region algorithm that provably converges to a local minimizer with from arbitrary initializations. Such minimizers give excellent approximations to rows of $\mathbf X_0$. The rows are then recovered by linear programming rounding and deflation.

Complete Dictionary Recovery over the Sphere I: Overview and the Geometric Picture

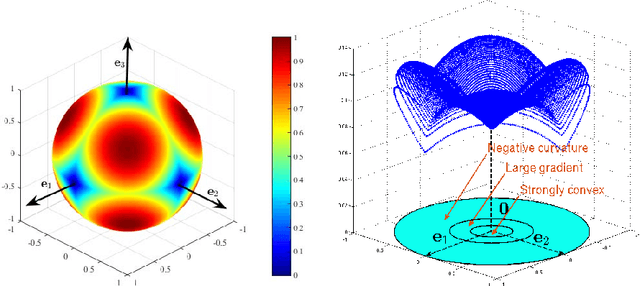
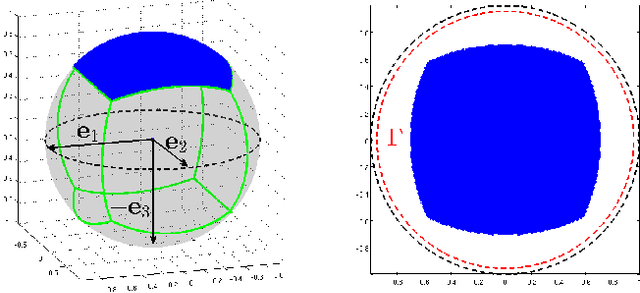
We consider the problem of recovering a complete (i.e., square and invertible) matrix $\mathbf A_0$, from $\mathbf Y \in \mathbb{R}^{n \times p}$ with $\mathbf Y = \mathbf A_0 \mathbf X_0$, provided $\mathbf X_0$ is sufficiently sparse. This recovery problem is central to theoretical understanding of dictionary learning, which seeks a sparse representation for a collection of input signals and finds numerous applications in modern signal processing and machine learning. We give the first efficient algorithm that provably recovers $\mathbf A_0$ when $\mathbf X_0$ has $O(n)$ nonzeros per column, under suitable probability model for $\mathbf X_0$. In contrast, prior results based on efficient algorithms either only guarantee recovery when $\mathbf X_0$ has $O(\sqrt{n})$ zeros per column, or require multiple rounds of SDP relaxation to work when $\mathbf X_0$ has $O(n^{1-\delta})$ nonzeros per column (for any constant $\delta \in (0, 1)$). } Our algorithmic pipeline centers around solving a certain nonconvex optimization problem with a spherical constraint. In this paper, we provide a geometric characterization of the objective landscape. In particular, we show that the problem is highly structured: with high probability, (1) there are no "spurious" local minimizers; and (2) around all saddle points the objective has a negative directional curvature. This distinctive structure makes the problem amenable to efficient optimization algorithms. In a companion paper (arXiv:1511.04777), we design a second-order trust-region algorithm over the sphere that provably converges to a local minimizer from arbitrary initializations, despite the presence of saddle points.

Finding a sparse vector in a subspace: Linear sparsity using alternating directions

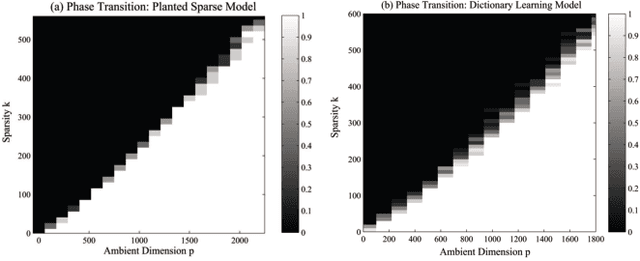
Is it possible to find the sparsest vector (direction) in a generic subspace $\mathcal{S} \subseteq \mathbb{R}^p$ with $\mathrm{dim}(\mathcal{S})= n < p$? This problem can be considered a homogeneous variant of the sparse recovery problem, and finds connections to sparse dictionary learning, sparse PCA, and many other problems in signal processing and machine learning. In this paper, we focus on a **planted sparse model** for the subspace: the target sparse vector is embedded in an otherwise random subspace. Simple convex heuristics for this planted recovery problem provably break down when the fraction of nonzero entries in the target sparse vector substantially exceeds $O(1/\sqrt{n})$. In contrast, we exhibit a relatively simple nonconvex approach based on alternating directions, which provably succeeds even when the fraction of nonzero entries is $\Omega(1)$. To the best of our knowledge, this is the first practical algorithm to achieve linear scaling under the planted sparse model. Empirically, our proposed algorithm also succeeds in more challenging data models, e.g., sparse dictionary learning.

When Are Nonconvex Problems Not Scary?

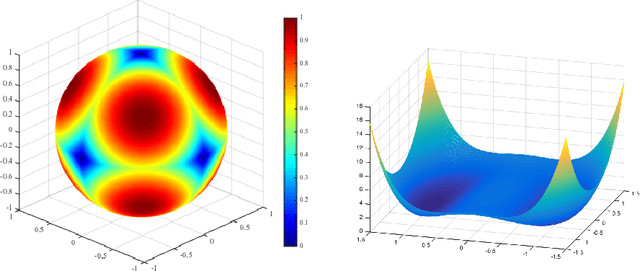
In this note, we focus on smooth nonconvex optimization problems that obey: (1) all local minimizers are also global; and (2) around any saddle point or local maximizer, the objective has a negative directional curvature. Concrete applications such as dictionary learning, generalized phase retrieval, and orthogonal tensor decomposition are known to induce such structures. We describe a second-order trust-region algorithm that provably converges to a global minimizer efficiently, without special initializations. Finally we highlight alternatives, and open problems in this direction.

Complete Dictionary Recovery over the Sphere

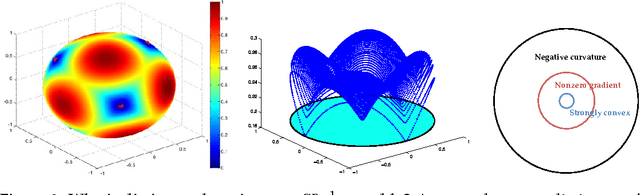
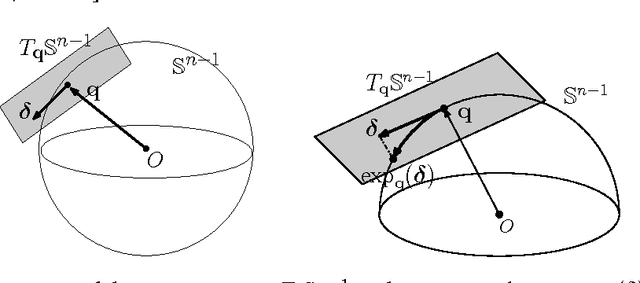
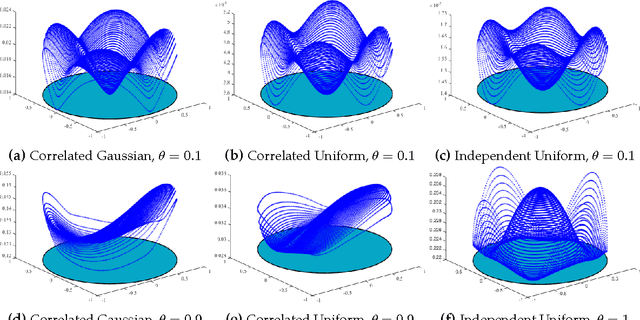
We consider the problem of recovering a complete (i.e., square and invertible) matrix $\mathbf A_0$, from $\mathbf Y \in \mathbb R^{n \times p}$ with $\mathbf Y = \mathbf A_0 \mathbf X_0$, provided $\mathbf X_0$ is sufficiently sparse. This recovery problem is central to the theoretical understanding of dictionary learning, which seeks a sparse representation for a collection of input signals, and finds numerous applications in modern signal processing and machine learning. We give the first efficient algorithm that provably recovers $\mathbf A_0$ when $\mathbf X_0$ has $O(n)$ nonzeros per column, under suitable probability model for $\mathbf X_0$. In contrast, prior results based on efficient algorithms provide recovery guarantees when $\mathbf X_0$ has only $O(n^{1-\delta})$ nonzeros per column for any constant $\delta \in (0, 1)$. Our algorithmic pipeline centers around solving a certain nonconvex optimization problem with a spherical constraint, and hence is naturally phrased in the language of manifold optimization. To show this apparently hard problem is tractable, we first provide a geometric characterization of the high-dimensional objective landscape, which shows that with high probability there are no "spurious" local minima. This particular geometric structure allows us to design a Riemannian trust region algorithm over the sphere that provably converges to one local minimizer with an arbitrary initialization, despite the presence of saddle points. The geometric approach we develop here may also shed light on other problems arising from nonconvex recovery of structured signals.

Efficient Point-to-Subspace Query in $\ell^1$ with Application to Robust Object Instance Recognition

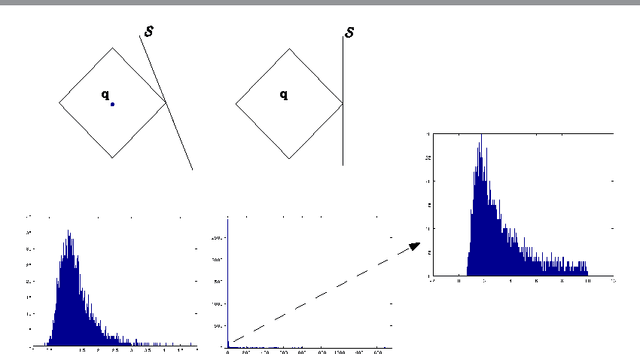
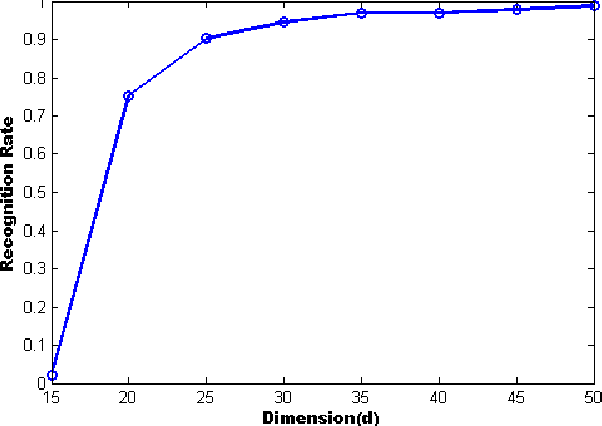
Motivated by vision tasks such as robust face and object recognition, we consider the following general problem: given a collection of low-dimensional linear subspaces in a high-dimensional ambient (image) space, and a query point (image), efficiently determine the nearest subspace to the query in $\ell^1$ distance. In contrast to the naive exhaustive search which entails large-scale linear programs, we show that the computational burden can be cut down significantly by a simple two-stage algorithm: (1) projecting the query and data-base subspaces into lower-dimensional space by random Cauchy matrix, and solving small-scale distance evaluations (linear programs) in the projection space to locate candidate nearest; (2) with few candidates upon independent repetition of (1), getting back to the high-dimensional space and performing exhaustive search. To preserve the identity of the nearest subspace with nontrivial probability, the projection dimension typically is low-order polynomial of the subspace dimension multiplied by logarithm of number of the subspaces (Theorem 2.1). The reduced dimensionality and hence complexity renders the proposed algorithm particularly relevant to vision application such as robust face and object instance recognition that we investigate empirically.

Efficient Point-to-Subspace Query in $\ell^1$: Theory and Applications in Computer Vision

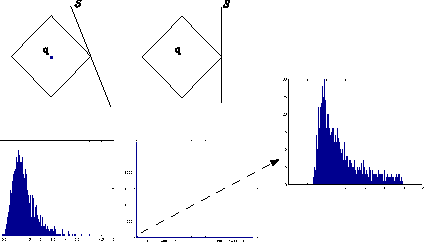
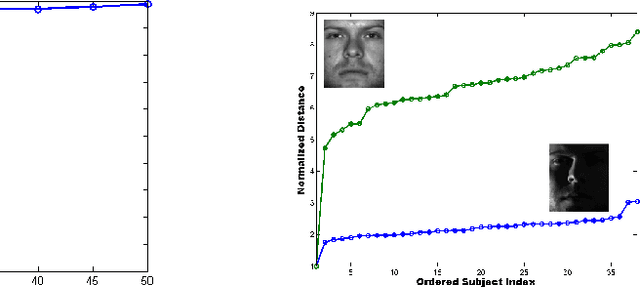
Motivated by vision tasks such as robust face and object recognition, we consider the following general problem: given a collection of low-dimensional linear subspaces in a high-dimensional ambient (image) space and a query point (image), efficiently determine the nearest subspace to the query in $\ell^1$ distance. We show in theory that Cauchy random embedding of the objects into significantly-lower-dimensional spaces helps preserve the identity of the nearest subspace with constant probability. This offers the possibility of efficiently selecting several candidates for accurate search. We sketch preliminary experiments on robust face and digit recognition to corroborate our theory.

Robust Recovery of Subspace Structures by Low-Rank Representation

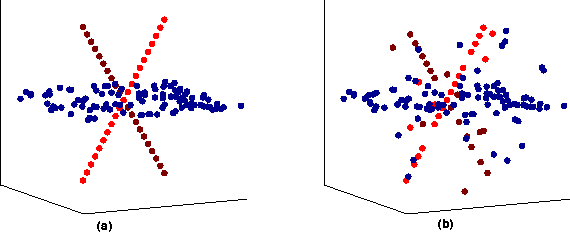
In this work we address the subspace recovery problem. Given a set of data samples (vectors) approximately drawn from a union of multiple subspaces, our goal is to segment the samples into their respective subspaces and correct the possible errors as well. To this end, we propose a novel method termed Low-Rank Representation (LRR), which seeks the lowest-rank representation among all the candidates that can represent the data samples as linear combinations of the bases in a given dictionary. It is shown that LRR well solves the subspace recovery problem: when the data is clean, we prove that LRR exactly captures the true subspace structures; for the data contaminated by outliers, we prove that under certain conditions LRR can exactly recover the row space of the original data and detect the outlier as well; for the data corrupted by arbitrary errors, LRR can also approximately recover the row space with theoretical guarantees. Since the subspace membership is provably determined by the row space, these further imply that LRR can perform robust subspace segmentation and error correction, in an efficient way.

Closed-Form Solutions to A Category of Nuclear Norm Minimization Problems

It is an efficient and effective strategy to utilize the nuclear norm approximation to learn low-rank matrices, which arise frequently in machine learning and computer vision. So the exploration of nuclear norm minimization problems is gaining much attention recently. In this paper we shall prove that the following Low-Rank Representation (LRR) \cite{icml_2010_lrr,lrr_extention} problem: {eqnarray*} \min_{Z} \norm{Z}_*, & {s.t.,} & X=AZ, {eqnarray*} has a unique and closed-form solution, where $X$ and $A$ are given matrices. The proof is based on proving a lemma that allows us to get closed-form solutions to a category of nuclear norm minimization problems.

Selective Image Super-Resolution

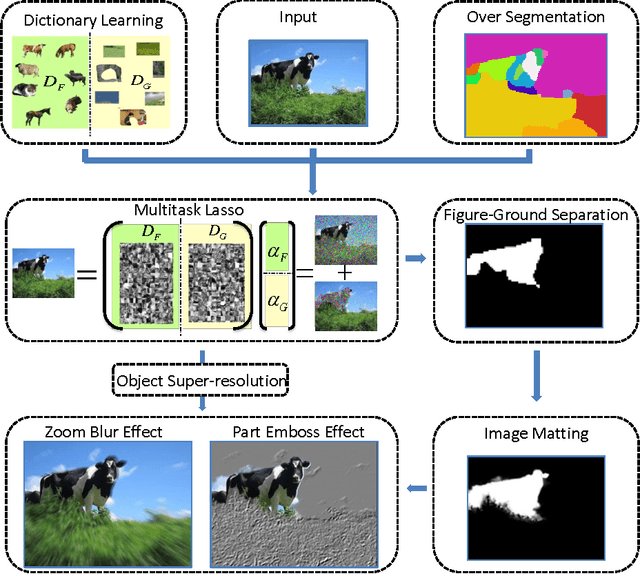
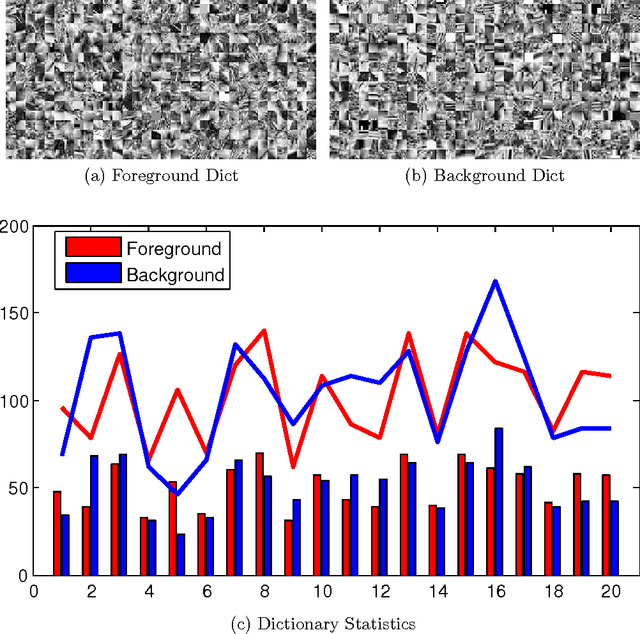
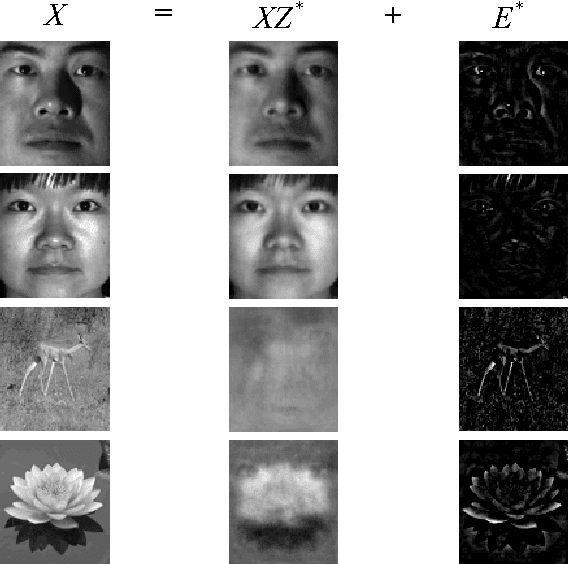
In this paper we propose a vision system that performs image Super Resolution (SR) with selectivity. Conventional SR techniques, either by multi-image fusion or example-based construction, have failed to capitalize on the intrinsic structural and semantic context in the image, and performed "blind" resolution recovery to the entire image area. By comparison, we advocate example-based selective SR whereby selectivity is exemplified in three aspects: region selectivity (SR only at object regions), source selectivity (object SR with trained object dictionaries), and refinement selectivity (object boundaries refinement using matting). The proposed system takes over-segmented low-resolution images as inputs, assimilates recent learning techniques of sparse coding (SC) and grouped multi-task lasso (GMTL), and leads eventually to a framework for joint figure-ground separation and interest object SR. The efficiency of our framework is manifested in our experiments with subsets of the VOC2009 and MSRC datasets. We also demonstrate several interesting vision applications that can build on our system.