Icebreaker: Element-wise Active Information Acquisition with Bayesian Deep Latent Gaussian Model

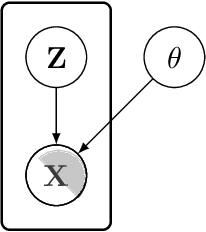
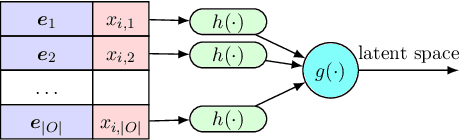
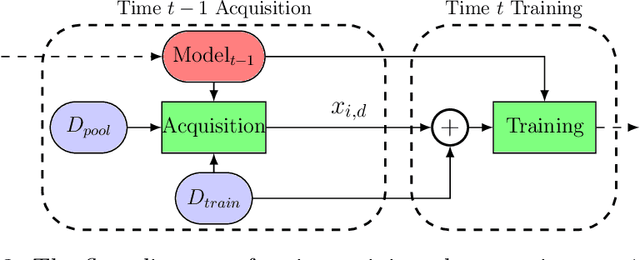
In this paper we introduce the ice-start problem, i.e., the challenge of deploying machine learning models when only little or no training data is initially available, and acquiring each feature element of data is associated with costs. This setting is representative for the real-world machine learning applications. For instance, in the health-care domain, when training an AI system for predicting patient metrics from lab tests, obtaining every single measurement comes with a high cost. Active learning, where only the label is associated with a cost does not apply to such problem, because performing all possible lab tests to acquire a new training datum would be costly, as well as unnecessary due to redundancy. We propose Icebreaker, a principled framework to approach the ice-start problem. Icebreaker uses a full Bayesian Deep Latent Gaussian Model (BELGAM) with a novel inference method. Our proposed method combines recent advances in amortized inference and stochastic gradient MCMC to enable fast and accurate posterior inference. By utilizing BELGAM's ability to fully quantify model uncertainty, we also propose two information acquisition functions for imputation and active prediction problems. We demonstrate that BELGAM performs significantly better than the previous VAE (Variational autoencoder) based models, when the data set size is small, using both machine learning benchmarks and real-world recommender systems and health-care applications. Moreover, based on BELGAM, Icebreaker further improves the performance and demonstrate the ability to use minimum amount of the training data to obtain the highest test time performance.

Bayesian Batch Active Learning as Sparse Subset Approximation

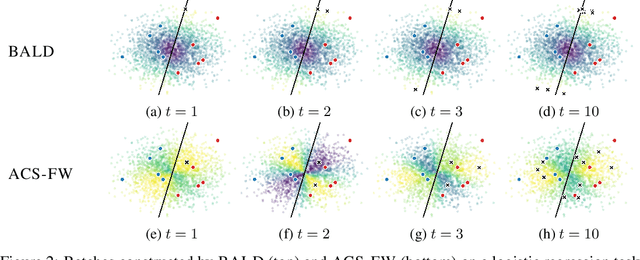
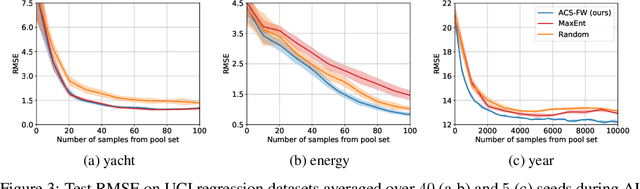
Leveraging the wealth of unlabeled data produced in recent years provides great potential for improving supervised models. When the cost of acquiring labels is high, probabilistic active learning methods can be used to greedily select the most informative data points to be labeled. However, for many large-scale problems standard greedy procedures become computationally infeasible and suffer from negligible model change. In this paper, we introduce a novel Bayesian batch active learning approach that mitigates these issues. Our approach is motivated by approximating the complete data posterior of the model parameters. While naive batch construction methods result in correlated queries, our algorithm produces diverse batches that enable efficient active learning at scale. We derive interpretable closed-form solutions akin to existing active learning procedures for linear models, and generalize to arbitrary models using random projections. We demonstrate the benefits of our approach on several large-scale regression and classification tasks.

'In-Between' Uncertainty in Bayesian Neural Networks

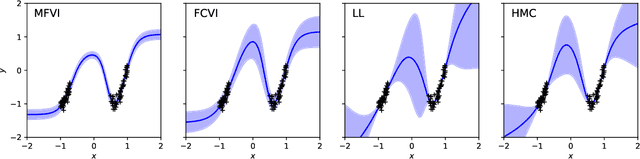
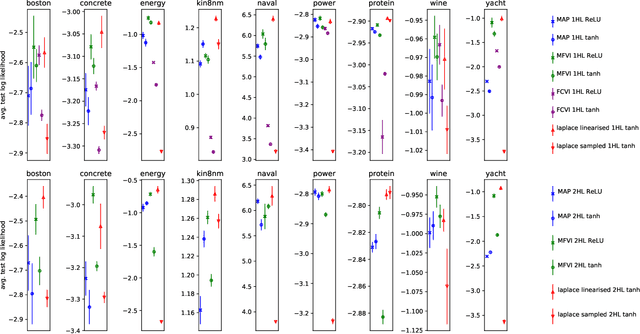
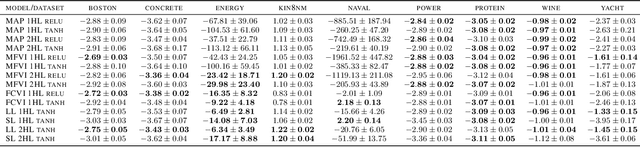
We describe a limitation in the expressiveness of the predictive uncertainty estimate given by mean-field variational inference (MFVI), a popular approximate inference method for Bayesian neural networks. In particular, MFVI fails to give calibrated uncertainty estimates in between separated regions of observations. This can lead to catastrophically overconfident predictions when testing on out-of-distribution data. Avoiding such overconfidence is critical for active learning, Bayesian optimisation and out-of-distribution robustness. We instead find that a classical technique, the linearised Laplace approximation, can handle 'in-between' uncertainty much better for small network architectures.

A Model to Search for Synthesizable Molecules

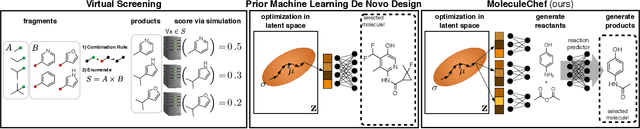
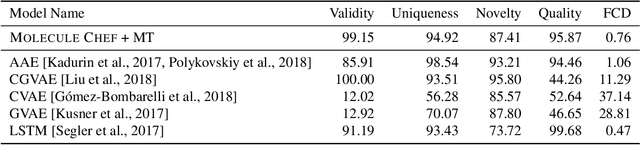
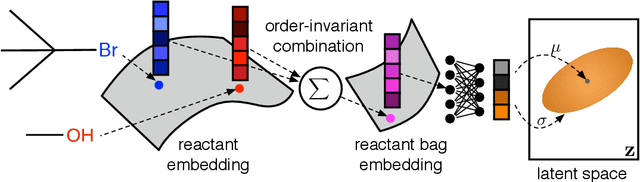
Deep generative models are able to suggest new organic molecules by generating strings, trees, and graphs representing their structure. While such models allow one to generate molecules with desirable properties, they give no guarantees that the molecules can actually be synthesized in practice. We propose a new molecule generation model, mirroring a more realistic real-world process, where (a) reactants are selected, and (b) combined to form more complex molecules. More specifically, our generative model proposes a bag of initial reactants (selected from a pool of commercially-available molecules) and uses a reaction model to predict how they react together to generate new molecules. We first show that the model can generate diverse, valid and unique molecules due to the useful inductive biases of modeling reactions. Furthermore, our model allows chemists to interrogate not only the properties of the generated molecules but also the feasibility of the synthesis routes. We conclude by using our model to solve retrosynthesis problems, predicting a set of reactants that can produce a target product.

A COLD Approach to Generating Optimal Samples

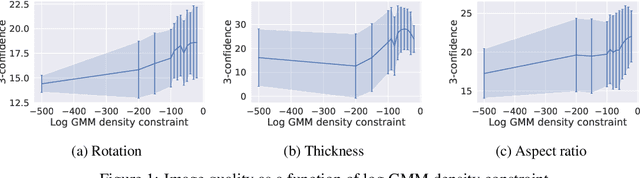
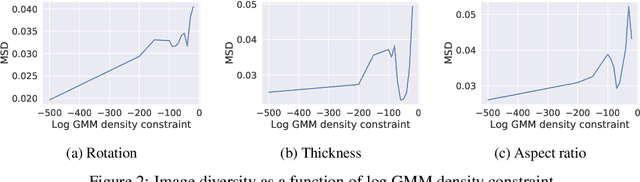
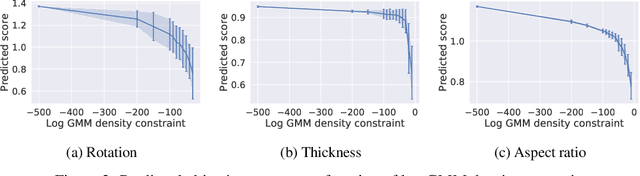
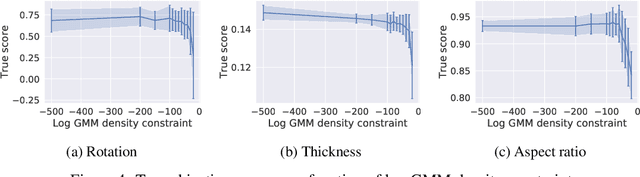
Optimising discrete data for a desired characteristic using gradient-based methods involves projecting the data into a continuous latent space and carrying out optimisation in this space. Carrying out global optimisation is difficult as optimisers are likely to follow gradients into regions of the latent space that the model has not been exposed to during training; samples generated from these regions are likely to be too dissimilar to the training data to be useful. We propose Constrained Optimisation with Latent Distributions (COLD), a constrained global optimisation procedure to find samples with high values of a desired property that are similar to yet distinct from the training data. We find that on MNIST, our procedure yields optima for each of three different objectives, and that enforcing tighter constraints improves the quality and increases the diversity of the generated images. On the ChEMBL molecular dataset, our method generates a diverse set of new molecules with drug-likeness scores similar to those of the highest-scoring molecules in the training data. We also demonstrate a computationally efficient way to approximate the constraint when evaluating it exactly is computationally expensive.

Interpretable Outcome Prediction with Sparse Bayesian Neural Networks in Intensive Care

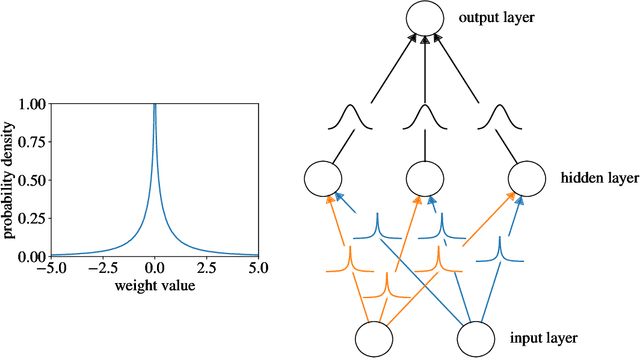
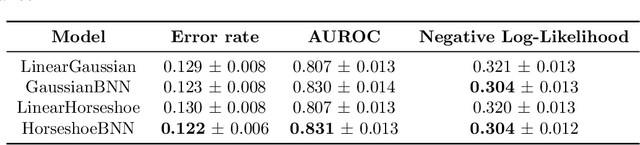
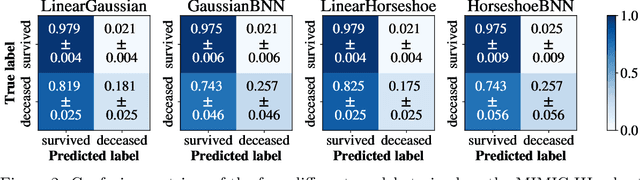
Clinical decision making is challenging because of pathological complexity, as well as large amounts of heterogeneous data generated as part of routine clinical care. In recent years, machine learning tools have been developed to aid this process. Intensive care unit (ICU) admissions represent the most data dense and time-critical patient care episodes. In this context, prediction models may help clinicians determine which patients are most at risk and prioritize care. However, flexible tools such as artificial neural networks (ANNs) suffer from a lack of interpretability limiting their acceptability to clinicians. In this work, we propose a novel interpretable Bayesian neural network architecture which offers both the flexibility of ANNs and interpretability in terms of feature selection. In particular, we employ a sparsity inducing prior distribution in a tied manner to learn which features are important for outcome prediction. We evaluate our approach on the task of mortality prediction using two real-world ICU cohorts. In collaboration with clinicians we found that, in addition to the predicted outcome results, our approach can provide novel insights into the importance of different clinical measurements. This suggests that our model can support medical experts in their decision making process.

Deconfounding Reinforcement Learning in Observational Settings

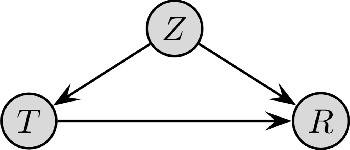
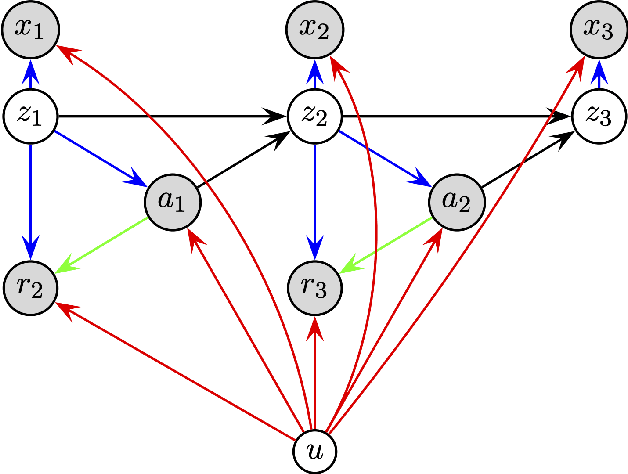
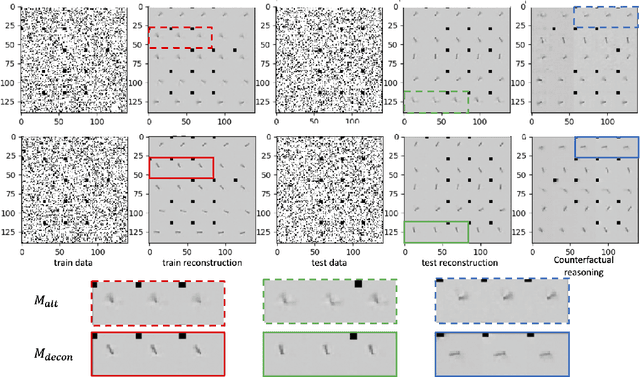
We propose a general formulation for addressing reinforcement learning (RL) problems in settings with observational data. That is, we consider the problem of learning good policies solely from historical data in which unobserved factors (confounders) affect both observed actions and rewards. Our formulation allows us to extend a representative RL algorithm, the Actor-Critic method, to its deconfounding variant, with the methodology for this extension being easily applied to other RL algorithms. In addition to this, we develop a new benchmark for evaluating deconfounding RL algorithms by modifying the OpenAI Gym environments and the MNIST dataset. Using this benchmark, we demonstrate that the proposed algorithms are superior to traditional RL methods in confounded environments with observational data. To the best of our knowledge, this is the first time that confounders are taken into consideration for addressing full RL problems with observational data. Code is available at https://github.com/CausalRL/DRL.

Learning a Generative Model for Validity in Complex Discrete Structures

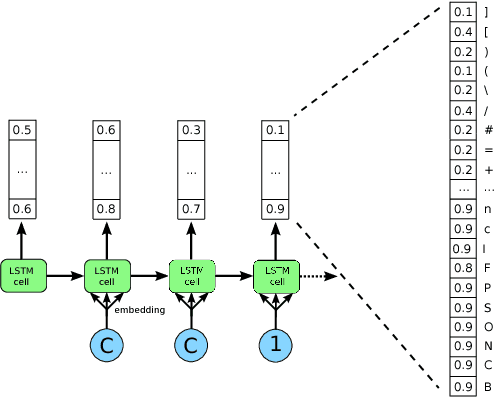
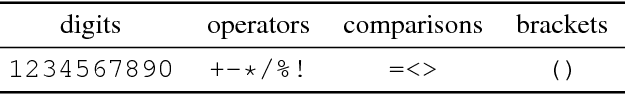
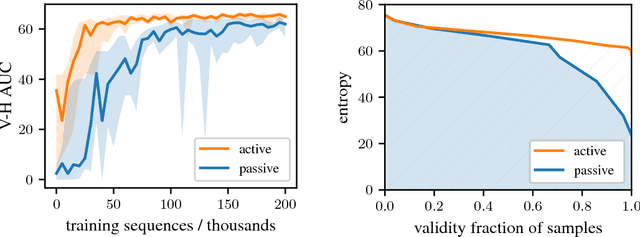
Deep generative models have been successfully used to learn representations for high-dimensional discrete spaces by representing discrete objects as sequences and employing powerful sequence-based deep models. Unfortunately, these sequence-based models often produce invalid sequences: sequences which do not represent any underlying discrete structure; invalid sequences hinder the utility of such models. As a step towards solving this problem, we propose to learn a deep recurrent validator model, which can estimate whether a partial sequence can function as the beginning of a full, valid sequence. This validator provides insight as to how individual sequence elements influence the validity of the overall sequence, and can be used to constrain sequence based models to generate valid sequences -- and thus faithfully model discrete objects. Our approach is inspired by reinforcement learning, where an oracle which can evaluate validity of complete sequences provides a sparse reward signal. We demonstrate its effectiveness as a generative model of Python 3 source code for mathematical expressions, and in improving the ability of a variational autoencoder trained on SMILES strings to decode valid molecular structures.

Successor Uncertainties: exploration and uncertainty in temporal difference learning

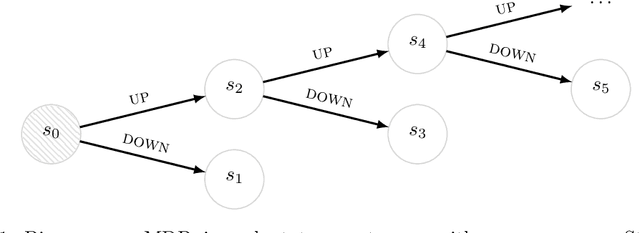
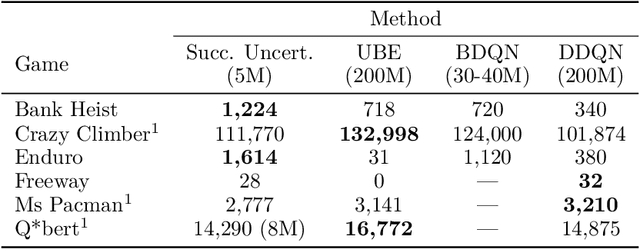
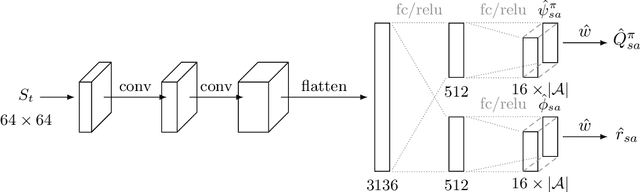
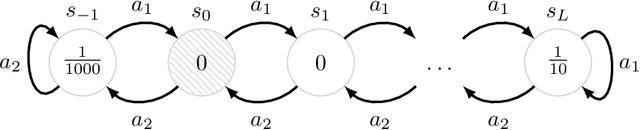
We consider the problem of balancing exploration and exploitation in sequential decision making problems. To explore efficiently, it is vital to consider the uncertainty over all consequences of a decision, and not just those that follow immediately; the uncertainties involved need to be propagated according to the dynamics of the problem. To this end, we develop Successor Uncertainties, a probabilistic model for the state-action value function of a Markov Decision Process that propagates uncertainties in a coherent and scalable way. We relate our approach to other classical and contemporary methods for exploration and present an empirical analysis.

EDDI: Efficient Dynamic Discovery of High-Value Information with Partial VAE

Making decisions requires information relevant to the task at hand. Many real-life decision-making situations allow acquiring further relevant information at a specific cost. For example, in assessing the health status of a patient we may decide to take additional measurements such as diagnostic tests or imaging scans before making a final assessment. More information that is relevant allows for better decisions but it may be costly to acquire all of this information. How can we trade off the desire to make good decisions with the option to acquire further information at a cost? To this end, we propose a principled framework, named EDDI (Efficient Dynamic Discovery of high-value Information), based on the theory of Bayesian experimental design. In EDDI we propose a novel partial variational autoencoder (Partial VAE), to efficiently handle missing data over varying subsets of known information. EDDI combines this Partial VAE with an acquisition function that maximizes expected information gain on a set of target variables. EDDI is efficient and demonstrates that dynamic discovery of high-value information is possible; we show cost reduction at the same decision quality and improved decision quality at the same cost in benchmarks and in two health-care applications. We believe there is great potential for realizing these gains in real-world decision support systems.