On-the-fly spectral unmixing based on Kalman filtering

This work introduces an on-the-fly (i.e., online) linear unmixing method which is able to sequentially analyze spectral data acquired on a spectrum-by-spectrum basis. After deriving a sequential counterpart of the conventional linear mixing model, the proposed approach recasts the linear unmixing problem into a linear state-space estimation framework. Under Gaussian noise and state models, the estimation of the pure spectra can be efficiently conducted by resorting to Kalman filtering. Interestingly, it is shown that this Kalman filter can operate in a lower-dimensional subspace while ensuring the nonnegativity constraint inherent to pure spectra. This dimensionality reduction allows significantly lightening the computational burden, while leveraging recent advances related to the representation of essential spectral information. The proposed method is evaluated through extensive numerical experiments conducted on synthetic and real Raman data sets. The results show that this Kalman filter-based method offers a convenient trade-off between unmixing accuracy and computational efficiency, which is crucial for operating in an on-the-fly setting. To the best of the authors' knowledge, this is the first operational method which is able to solve the spectral unmixing problem efficiently in a dynamic fashion. It also constitutes a valuable building block for benefiting from acquisition and processing frameworks recently proposed in the microscopy literature, which are motivated by practical issues such as reducing acquisition time and avoiding potential damages being inflicted to photosensitive samples.

Performance Gaps in Multi-view Clustering under the Nested Matrix-Tensor Model

We study the estimation of a planted signal hidden in a recently introduced nested matrix-tensor model, which is an extension of the classical spiked rank-one tensor model, motivated by multi-view clustering. Prior work has theoretically examined the performance of a tensor-based approach, which relies on finding a best rank-one approximation, a problem known to be computationally hard. A tractable alternative approach consists in computing instead the best rank-one (matrix) approximation of an unfolding of the observed tensor data, but its performance was hitherto unknown. We quantify here the performance gap between these two approaches, in particular by deriving the precise algorithmic threshold of the unfolding approach and demonstrating that it exhibits a BBP-type transition behavior. This work is therefore in line with recent contributions which deepen our understanding of why tensor-based methods surpass matrix-based methods in handling structured tensor data.

On the Accuracy of Hotelling-Type Asymmetric Tensor Deflation: A Random Tensor Analysis

This work introduces an asymptotic study of Hotelling-type tensor deflation in the presence of noise, in the regime of large tensor dimensions. Specifically, we consider a low-rank asymmetric tensor model of the form $\sum_{i=1}^r \beta_i{\mathcal{A}}_i + {\mathcal{W}}$ where $\beta_i\geq 0$ and the ${\mathcal{A}}_i$'s are unit-norm rank-one tensors such that $\left| \langle {\mathcal{A}}_i, {\mathcal{A}}_j \rangle \right| \in [0, 1]$ for $i\neq j$ and ${\mathcal{W}}$ is an additive noise term. Assuming that the dominant components are successively estimated from the noisy observation and subsequently subtracted, we leverage recent advances in random tensor theory in the regime of asymptotically large tensor dimensions to analytically characterize the estimated singular values and the alignment of estimated and true singular vectors at each step of the deflation procedure. Furthermore, this result can be used to construct estimators of the signal-to-noise ratios $\beta_i$ and the alignments between the estimated and true rank-1 signal components.

Hotelling Deflation on Large Symmetric Spiked Tensors

This paper studies the deflation algorithm when applied to estimate a low-rank symmetric spike contained in a large tensor corrupted by additive Gaussian noise. Specifically, we provide a precise characterization of the large-dimensional performance of deflation in terms of the alignments of the vectors obtained by successive rank-1 approximation and of their estimated weights, assuming non-trivial (fixed) correlations among spike components. Our analysis allows an understanding of the deflation mechanism in the presence of noise and can be exploited for designing more efficient signal estimation methods.

Majorization-minimization for Sparse Nonnegative Matrix Factorization with the $β$-divergence

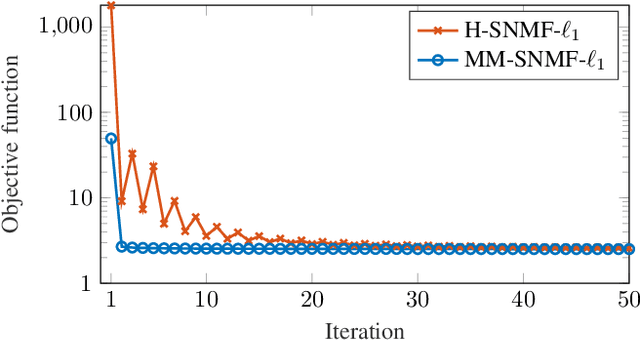
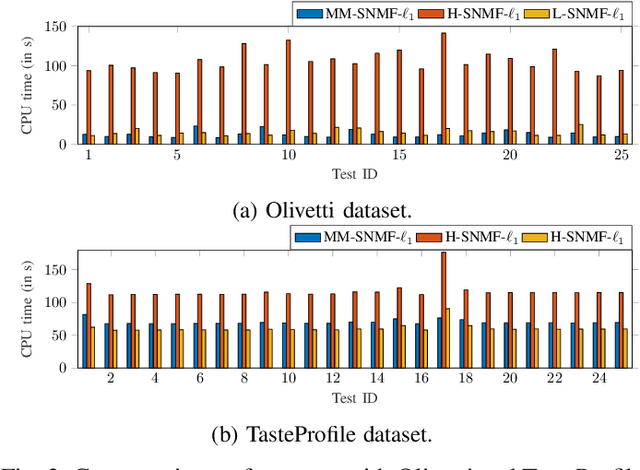
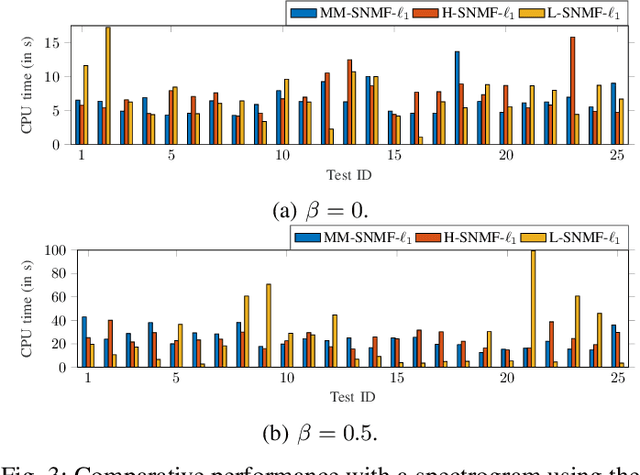
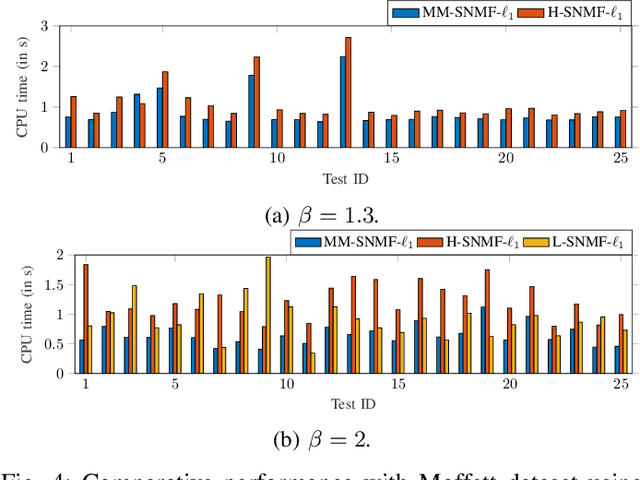
This article introduces new multiplicative updates for nonnegative matrix factorization with the $\beta$-divergence and sparse regularization of one of the two factors (say, the activation matrix). It is well known that the norm of the other factor (the dictionary matrix) needs to be controlled in order to avoid an ill-posed formulation. Standard practice consists in constraining the columns of the dictionary to have unit norm, which leads to a nontrivial optimization problem. Our approach leverages a reparametrization of the original problem into the optimization of an equivalent scale-invariant objective function. From there, we derive block-descent majorization-minimization algorithms that result in simple multiplicative updates for either $\ell_{1}$-regularization or the more "aggressive" log-regularization. In contrast with other state-of-the-art methods, our algorithms are universal in the sense that they can be applied to any $\beta$-divergence (i.e., any value of $\beta$) and that they come with convergence guarantees. We report numerical comparisons with existing heuristic and Lagrangian methods using various datasets: face images, an audio spectrogram, hyperspectral data, and song play counts. We show that our methods obtain solutions of similar quality at convergence (similar objective values) but with significantly reduced CPU times.

COL0RME: Super-resolution microscopy based on sparse blinking fluorophore localization and intensity estimation

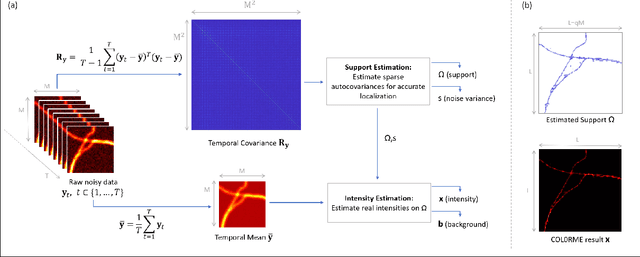
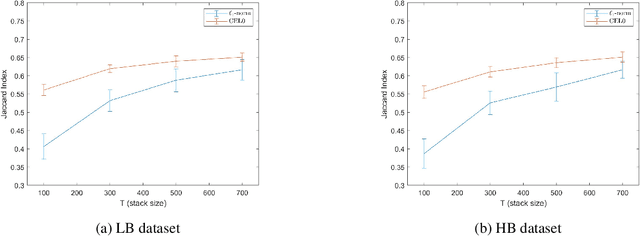
To overcome the physical barriers caused by light diffraction, super-resolution techniques are often applied in fluorescent microscopy. State-of-the-art approaches require specific and often demanding acquisition conditions to achieve adequate levels of both spatial and temporal resolution. Analyzing the stochastic fluctuations of the fluorescent molecules provides a solution to the aforementioned limitations, as sufficiently high spatio-temporal resolution for live-cell imaging can be achieved by using common microscopes and conventional fluorescent dyes. Based on this idea, we present COL0RME, a method for COvariance-based $\ell_0$ super-Resolution Microscopy with intensity Estimation, which achieves good spatio-temporal resolution by solving a sparse optimization problem in the covariance domain, and discuss automatic parameter selection strategies. The method is composed of two steps: the former where both the emitters' independence and the sparse distribution of the fluorescent molecules are exploited to provide an accurate localization; the latter where real intensity values are estimated given the computed support. The paper is furnished with several numerical results both on synthetic and real fluorescent microscopy images and several comparisons with state-of-the art approaches are provided. Our results show that COL0RME outperforms competing methods exploiting analogously temporal fluctuations; in particular, it achieves better localization, reduces background artifacts and avoids fine parameter tuning.

A Random Matrix Perspective on Random Tensors

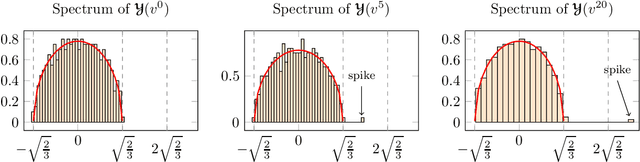
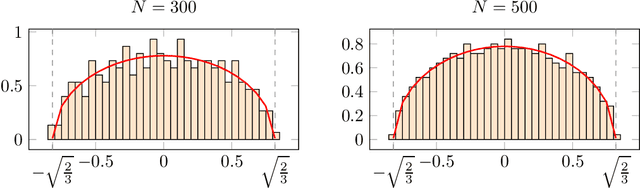
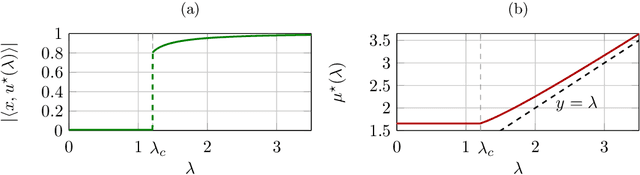
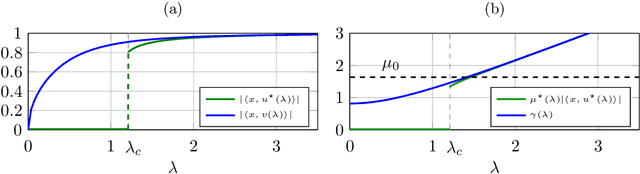
Tensor models play an increasingly prominent role in many fields, notably in machine learning. In several applications of such models, such as community detection, topic modeling and Gaussian mixture learning, one must estimate a low-rank signal from a noisy tensor. Hence, understanding the fundamental limits and the attainable performance of estimators of that signal inevitably calls for the study of random tensors. Substantial progress has been achieved on this subject thanks to recent efforts, under the assumption that the tensor dimensions grow large. Yet, some of the most significant among these results--in particular, a precise characterization of the abrupt phase transition (in terms of signal-to-noise ratio) that governs the performance of the maximum likelihood (ML) estimator of a symmetric rank-one model with Gaussian noise--were derived on the basis of statistical physics ideas, which are not easily accessible to non-experts. In this work, we develop a sharply distinct approach, relying instead on standard but powerful tools brought by years of advances in random matrix theory. The key idea is to study the spectra of random matrices arising from contractions of a given random tensor. We show how this gives access to spectral properties of the random tensor itself. In the specific case of a symmetric rank-one model with Gaussian noise, our technique yields a hitherto unknown characterization of the local maximum of the ML problem that is global above the phase transition threshold. This characterization is in terms of a fixed-point equation satisfied by a formula that had only been previously obtained via statistical physics methods. Moreover, our analysis sheds light on certain properties of the landscape of the ML problem in the large-dimensional setting. Our approach is versatile and can be extended to other models, such as asymmetric, non-Gaussian and higher-order ones.

On the Realization of Impulse Invariant Bilinear Volterra Kernels

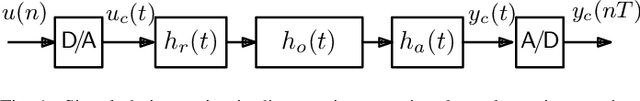
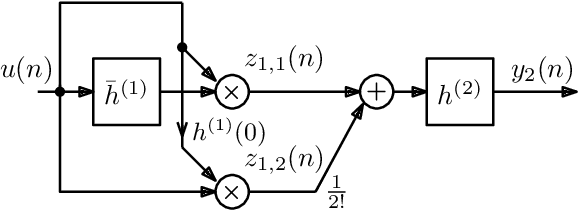
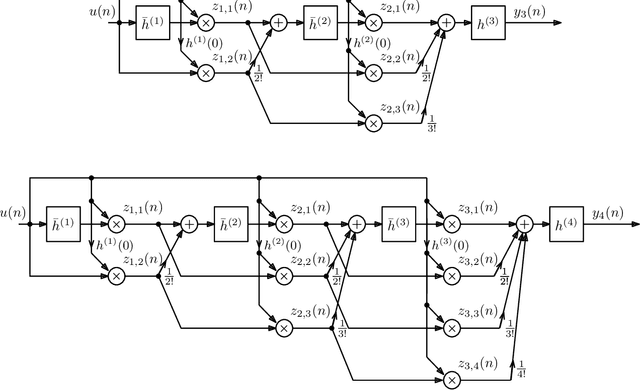
As previously shown, the direct extension of the impulse invariance principle to Volterra kernels has to be modified in order to provide a condition for the exact modeling of mixed-signal chains. At first sight this would seem to seriously complicate the otherwise simple discrete-time realization of separable kernels (among which bilinear kernels are of particular importance). We show here, however, that this not the case. By defining a cascade operator, the structure of a generalized impulse invariance can be unveiled, leading to a realization without an inordinate increase in computational complexity.

Joint Majorization-Minimization for Nonnegative Matrix Factorization with the $β$-divergence

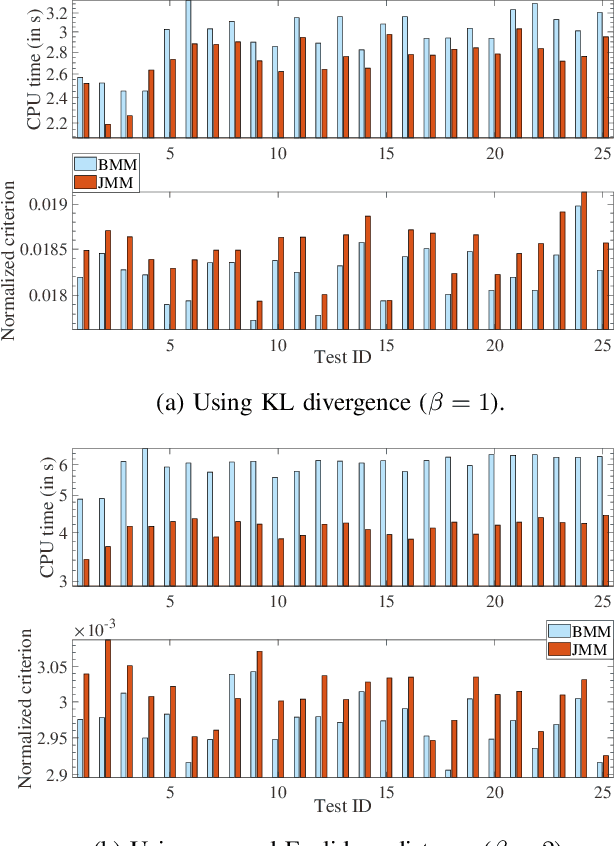
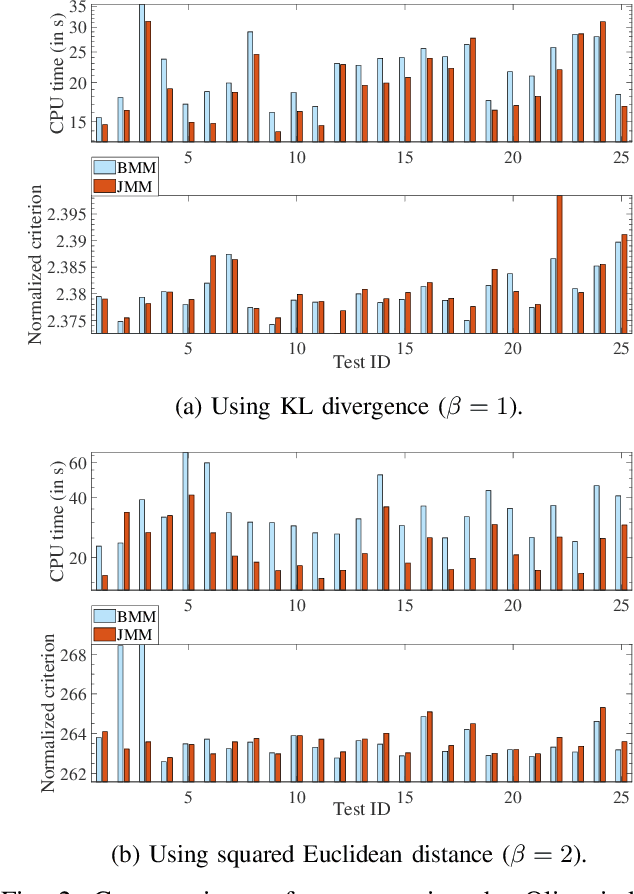
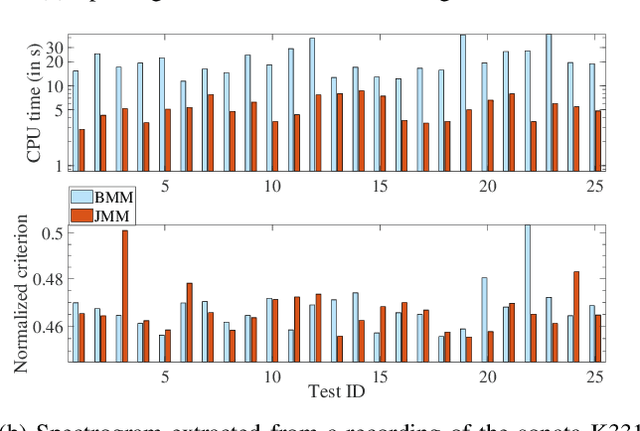
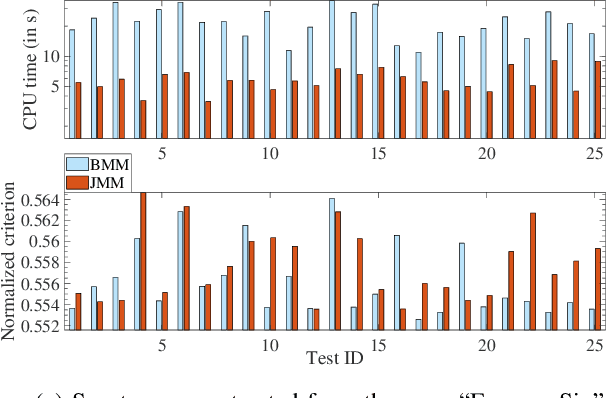
This article proposes new multiplicative updates for nonnegative matrix factorization (NMF) with the $\beta$-divergence objective function. Our new updates are derived from a joint majorization-minimization (MM) scheme, in which an auxiliary function (a tight upper bound of the objective function) is built for the two factors jointly and minimized at each iteration. This is in contrast with the classic approach in which the factors are optimized alternately and a MM scheme is applied to each factor individually. Like the classic approach, our joint MM algorithm also results in multiplicative updates that are simple to implement. They however yield a significant drop of computation time (for equally good solutions), in particular for some $\beta$-divergences of important applicative interest, such as the squared Euclidean distance and the Kullback-Leibler or Itakura-Saito divergences. We report experimental results using diverse datasets: face images, audio spectrograms, hyperspectral data and song play counts. Depending on the value of $\beta$ and on the dataset, our joint MM approach yields a CPU time reduction of about $10\%$ to $78\%$ in comparison to the classic alternating scheme.