Statistical Limits in Random Tensors with Multiple Correlated Spikes

We use tools from random matrix theory to study the multi-spiked tensor model, i.e., a rank-$r$ deformation of a symmetric random Gaussian tensor. In particular, thanks to the nature of local optimization methods used to find the maximum likelihood estimator of this model, we propose to study the phase transition phenomenon for finding critical points of the corresponding optimization problem, i.e., those points defined by the Karush-Kuhn-Tucker (KKT) conditions. Moreover, we characterize the limiting alignments between the estimated signals corresponding to a critical point of the likelihood and the ground truth signals. With the help of these results, we propose a new estimator of the rank-$r$ tensor weights by solving a system of polynomial equations, which is asymptotically unbiased contrary the maximum likelihood estimator.

An Introduction to Complex Random Tensors

This work considers the notion of random tensors and reviews some fundamental concepts in statistics when applied to a tensor based data or signal. In several engineering fields such as Communications, Signal Processing, Machine learning, and Control systems, the concepts of linear algebra combined with random variables have been indispensable tools. With the evolution of these subjects to multi-domain communication systems, multi-way signal processing, high dimensional data analysis, and multi-linear systems theory, there is a need to bring in multi-linear algebra equipped with the notion of random tensors. Also, since several such application areas deal with complex-valued entities, it is imperative to study this subject from a complex random tensor perspective, which is the focus of this paper. Using tools from multi-linear algebra, we characterize statistical properties of complex random tensors, both proper and improper, study various correlation structures, and fundamentals of tensor valued random processes. Furthermore, the asymptotic distribution of various tensor eigenvalue and singular value definitions is also considered, which is used for the study of spiked real tensor models that deals with recovery of low rank tensor signals perturbed by noise. This paper aims to provide an overview of the state of the art in random tensor theory of both complex and real valued tensors, for the purpose of enabling its application in engineering and applied science.

On the Accuracy of Hotelling-Type Asymmetric Tensor Deflation: A Random Tensor Analysis

This work introduces an asymptotic study of Hotelling-type tensor deflation in the presence of noise, in the regime of large tensor dimensions. Specifically, we consider a low-rank asymmetric tensor model of the form $\sum_{i=1}^r \beta_i{\mathcal{A}}_i + {\mathcal{W}}$ where $\beta_i\geq 0$ and the ${\mathcal{A}}_i$'s are unit-norm rank-one tensors such that $\left| \langle {\mathcal{A}}_i, {\mathcal{A}}_j \rangle \right| \in [0, 1]$ for $i\neq j$ and ${\mathcal{W}}$ is an additive noise term. Assuming that the dominant components are successively estimated from the noisy observation and subsequently subtracted, we leverage recent advances in random tensor theory in the regime of asymptotically large tensor dimensions to analytically characterize the estimated singular values and the alignment of estimated and true singular vectors at each step of the deflation procedure. Furthermore, this result can be used to construct estimators of the signal-to-noise ratios $\beta_i$ and the alignments between the estimated and true rank-1 signal components.

Unsourced Random Access With Tensor-Based and Coherent Modulations

Unsourced random access (URA) is a particular form of grant-free uncoordinated random access wherein the users' identities are not associated to specific waveforms at the physical layer. Tensor-based modulation (TBM) has been recently advocated as a promising technique for URA due to its ability to support a large number of active users transmitting simultaneously by exploiting tensor decomposition for user separation. We propose a novel URA scheme that builds upon TBM by splitting the transmit message into two sub-messages. This first part is modulated according to a TBM scheme, while the second is encoded using a coherent non-orthogonal multiple access (NOMA) modulation. At the receiver side, we exploit the advantages of forward error correction (FEC) coding and interference cancellation techniques. We compare the performances of the introduced scheme with state-of-the-art URA schemes under a quasi-static Rayleigh fading model, proving the energy efficiency and the fading robustness of the proposed solution.

On the Accuracy of Hotelling-Type Tensor Deflation: A Random Tensor Analysis

Leveraging on recent advances in random tensor theory, we consider in this paper a rank-$r$ asymmetric spiked tensor model of the form $\sum_{i=1}^r \beta_i A_i + W$ where $\beta_i\geq 0$ and the $A_i$'s are rank-one tensors such that $\langle A_i, A_j \rangle\in [0, 1]$ for $i\neq j$, based on which we provide an asymptotic study of Hotelling-type tensor deflation in the large dimensional regime. Specifically, our analysis characterizes the singular values and alignments at each step of the deflation procedure, for asymptotically large tensor dimensions. This can be used to construct consistent estimators of different quantities involved in the underlying problem, such as the signal-to-noise ratios $\beta_i$ or the alignments between the different signal components $\langle A_i, A_j \rangle$.

Constant Weight Codes with Gabor Dictionaries and Bayesian Decoding for Massive Random Access

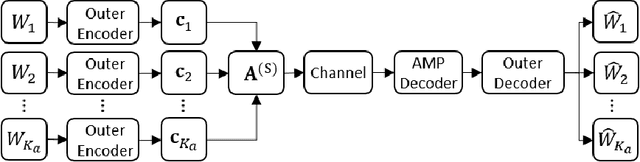
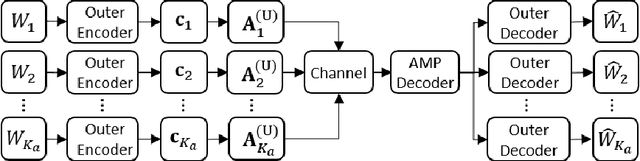
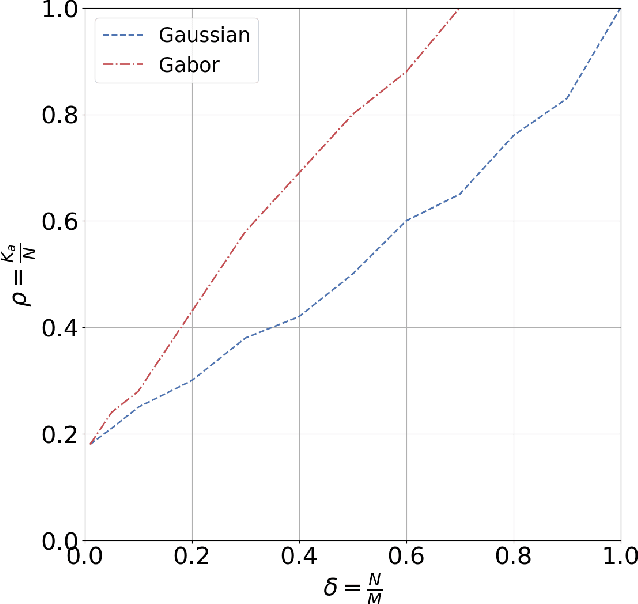
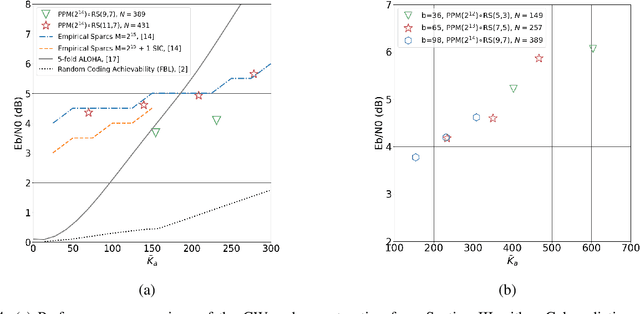
This paper considers a general framework for massive random access based on sparse superposition coding. We provide guidelines for the code design and propose the use of constant-weight codes in combination with a dictionary design based on Gabor frames. The decoder applies an extension of approximate message passing (AMP) by iteratively exchanging soft information between an AMP module that accounts for the dictionary structure, and a second inference module that utilizes the structure of the involved constant-weight code. We apply the encoding structure to (i) the unsourced random access setting, where all users employ a common dictionary, and (ii) to the "sourced" random access setting with user-specific dictionaries. When applied to a fading scenario, the communication scheme essentially operates non-coherently, as channel state information is required neither at the transmitter nor at the receiver. We observe that in regimes of practical interest, the proposed scheme compares favorably with state-of-the art schemes, in terms of the (per-user) energy-per-bit requirement, as well as the number of active users that can be simultaneously accommodated in the system. Importantly, this is achieved with a considerably smaller size of the transmitted codewords, potentially yielding lower latency and bandwidth occupancy, as well as lower implementation complexity.

Triplet-Based Wireless Channel Charting

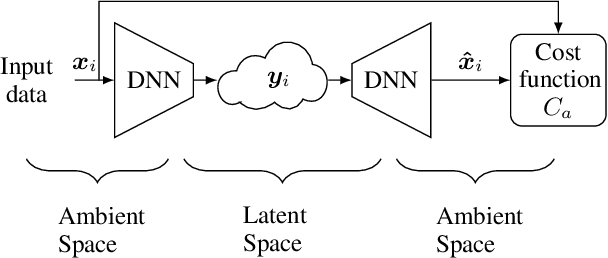
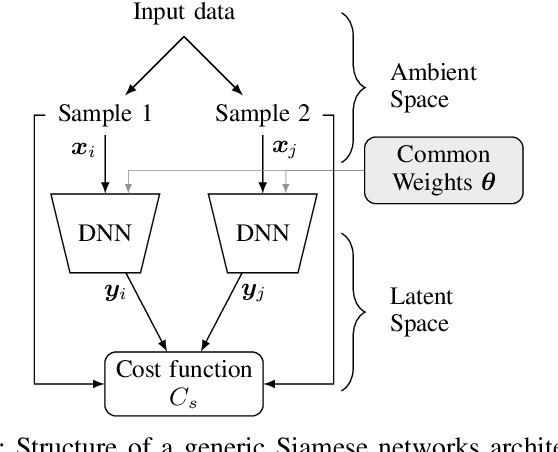
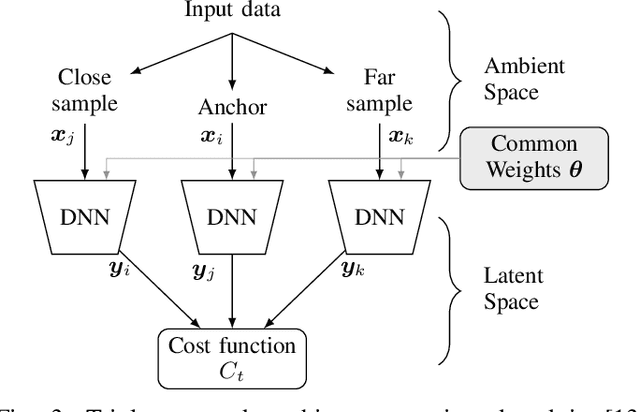
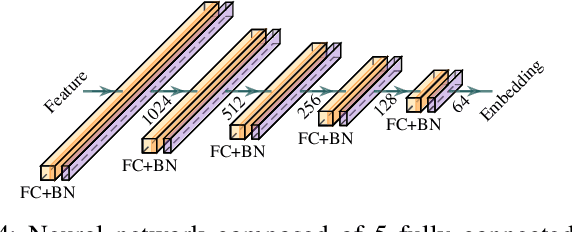
Channel charting is a data-driven baseband processing technique consisting in applying unsupervised machine learning techniques to channel state information (CSI), with the objective of reducing the dimension of the data and extracting the fundamental parameters governing the distribution of CSI samples observed by a given receiver. In this work, we focus on neural network-based approaches, and propose a new architecture based on triplets of samples. It allows to simultaneously learn a meaningful similarity metric between CSI samples, on the basis of proximity in their respective acquisition times, and to perform the sought dimensionality reduction. The proposed approach is evaluated on a dataset of measured massive MIMO CSI, and is shown to perform well in comparison to the state-of-the-art methods (UMAP, autoencoders and siamese networks). In particular, we show that the obtained chart representation is topologically close to the geographical user position, despite the fact that the charting approach is not supervised by any geographical data.

DNN-based Localization from Channel Estimates: Feature Design and Experimental Results

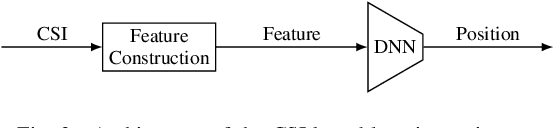
We consider the use of deep neural networks (DNNs) in the context of channel state information (CSI)-based localization for Massive MIMO cellular systems. We discuss the practical impairments that are likely to be present in practical CSI estimates, and introduce a principled approach to feature design for CSI-based DNN applications based on the objective of making the features invariant to the considered impairments. We demonstrate the efficiency of this approach by applying it to a dataset constituted of geo-tagged CSI measured in an outdoors campus environment, and training a DNN to estimate the position of the UE on the basis of the CSI. We provide an experimental evaluation of several aspects of that learning approach, including localization accuracy, generalization capability, and data aging.

CSI-based Outdoor Localization for Massive MIMO: Experiments with a Learning Approach

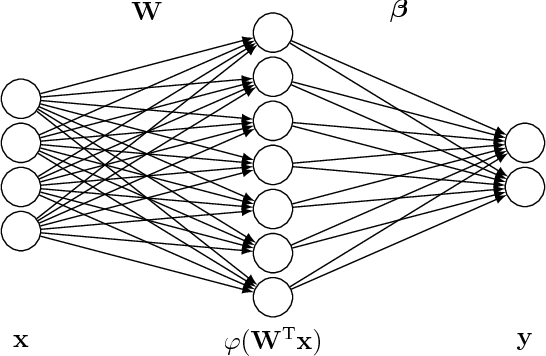
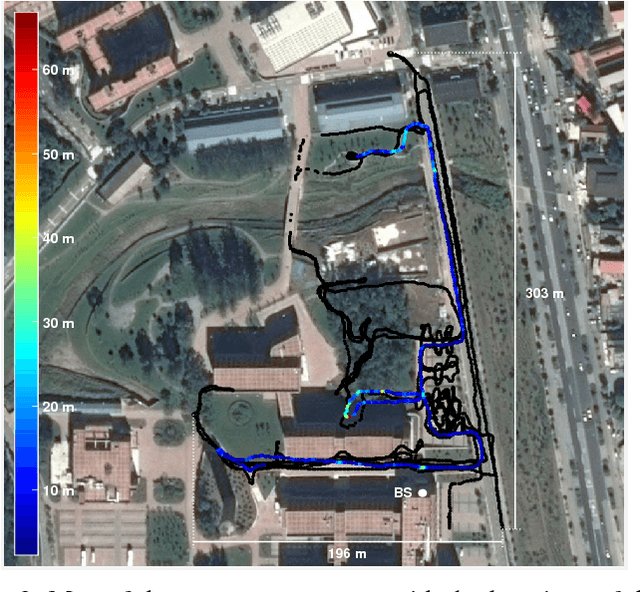
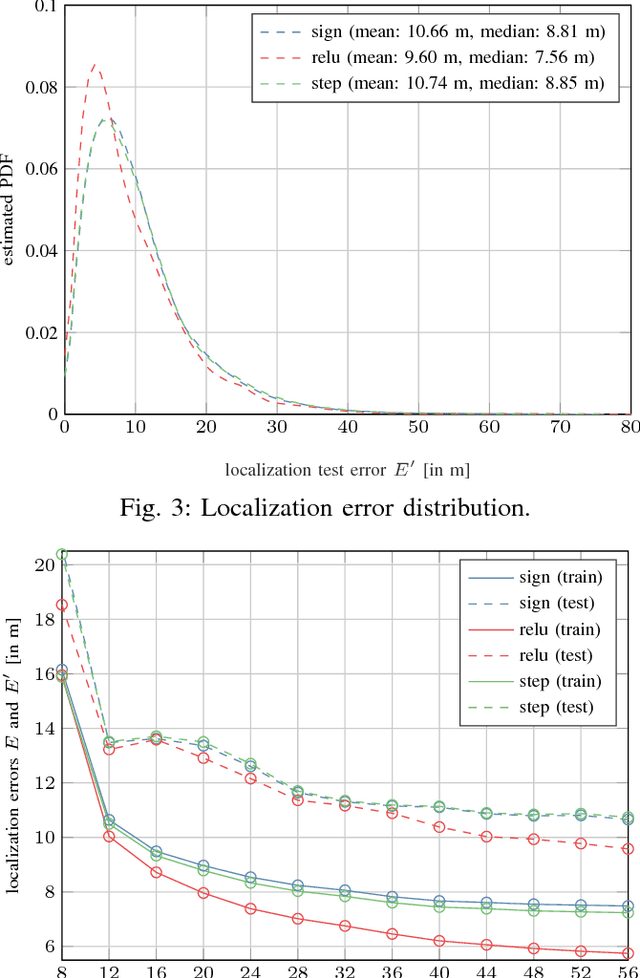
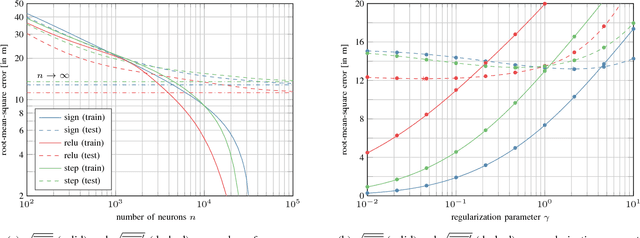
We report on experimental results on the use of a learning-based approach to infer the location of a mobile user of a cellular network within a cell, for a 5G-type Massive multiple input, multiple output (MIMO) system. We describe how the sample spatial covariance matrix computed from the CSI can be used as the input to a learning algorithm which attempts to relate it to user location. We discuss several learning approaches, and analyze in depth the application of extreme learning machines, for which theoretical approximate performance benchmarks are available, to the localization problem. We validate the proposed approach using experimental data collected on a Huawei 5G testbed, provide some performance and robustness benchmarks, and discuss practical issues related to the deployment of such a technique in 5G networks.