A Random Matrix Perspective on Random Tensors

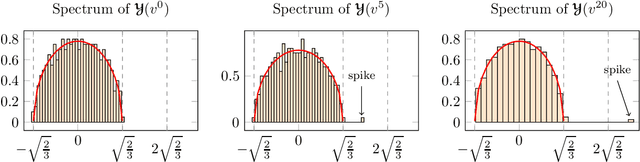
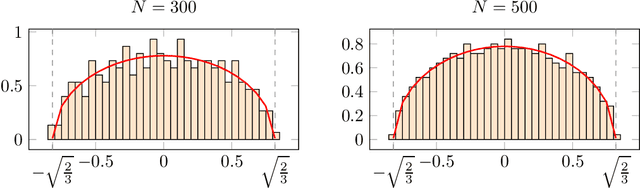
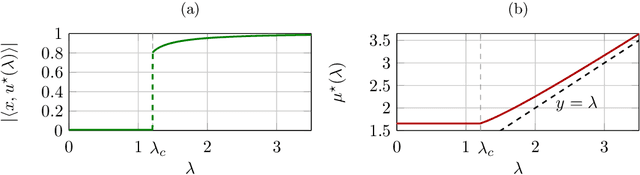
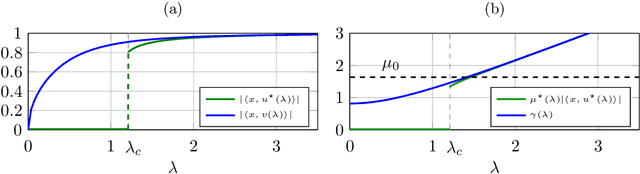
Tensor models play an increasingly prominent role in many fields, notably in machine learning. In several applications of such models, such as community detection, topic modeling and Gaussian mixture learning, one must estimate a low-rank signal from a noisy tensor. Hence, understanding the fundamental limits and the attainable performance of estimators of that signal inevitably calls for the study of random tensors. Substantial progress has been achieved on this subject thanks to recent efforts, under the assumption that the tensor dimensions grow large. Yet, some of the most significant among these results--in particular, a precise characterization of the abrupt phase transition (in terms of signal-to-noise ratio) that governs the performance of the maximum likelihood (ML) estimator of a symmetric rank-one model with Gaussian noise--were derived on the basis of statistical physics ideas, which are not easily accessible to non-experts. In this work, we develop a sharply distinct approach, relying instead on standard but powerful tools brought by years of advances in random matrix theory. The key idea is to study the spectra of random matrices arising from contractions of a given random tensor. We show how this gives access to spectral properties of the random tensor itself. In the specific case of a symmetric rank-one model with Gaussian noise, our technique yields a hitherto unknown characterization of the local maximum of the ML problem that is global above the phase transition threshold. This characterization is in terms of a fixed-point equation satisfied by a formula that had only been previously obtained via statistical physics methods. Moreover, our analysis sheds light on certain properties of the landscape of the ML problem in the large-dimensional setting. Our approach is versatile and can be extended to other models, such as asymmetric, non-Gaussian and higher-order ones.