John Lafferty
University of Chicago
A Convergent Gradient Descent Algorithm for Rank Minimization and Semidefinite Programming from Random Linear Measurements
Mar 24, 2016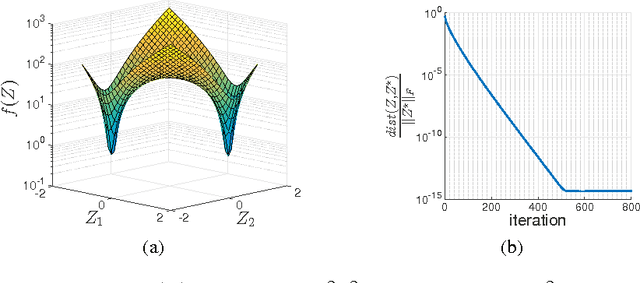

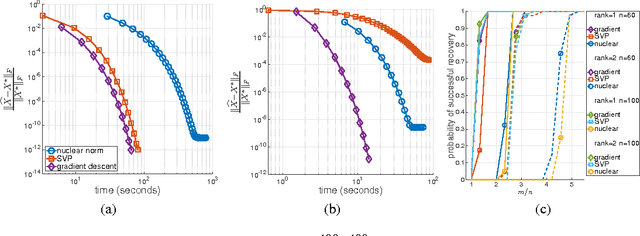
Abstract:We propose a simple, scalable, and fast gradient descent algorithm to optimize a nonconvex objective for the rank minimization problem and a closely related family of semidefinite programs. With $O(r^3 \kappa^2 n \log n)$ random measurements of a positive semidefinite $n \times n$ matrix of rank $r$ and condition number $\kappa$, our method is guaranteed to converge linearly to the global optimum.
Faithful Variable Screening for High-Dimensional Convex Regression
Nov 18, 2014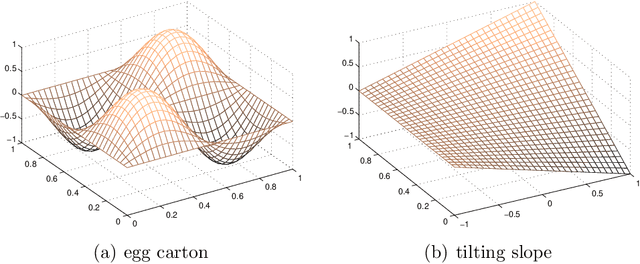
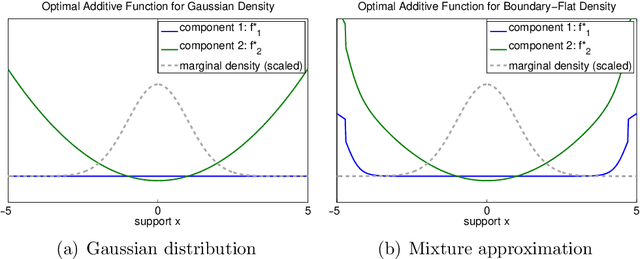
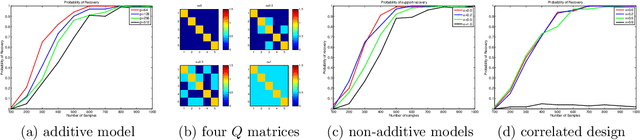
Abstract:We study the problem of variable selection in convex nonparametric regression. Under the assumption that the true regression function is convex and sparse, we develop a screening procedure to select a subset of variables that contains the relevant variables. Our approach is a two-stage quadratic programming method that estimates a sum of one-dimensional convex functions, followed by one-dimensional concave regression fits on the residuals. In contrast to previous methods for sparse additive models, the optimization is finite dimensional and requires no tuning parameters for smoothness. Under appropriate assumptions, we prove that the procedure is faithful in the population setting, yielding no false negatives. We give a finite sample statistical analysis, and introduce algorithms for efficiently carrying out the required quadratic programs. The approach leads to computational and statistical advantages over fitting a full model, and provides an effective, practical approach to variable screening in convex regression.
Quantized Estimation of Gaussian Sequence Models in Euclidean Balls
Sep 24, 2014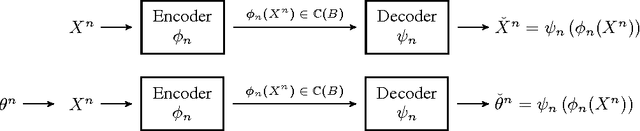
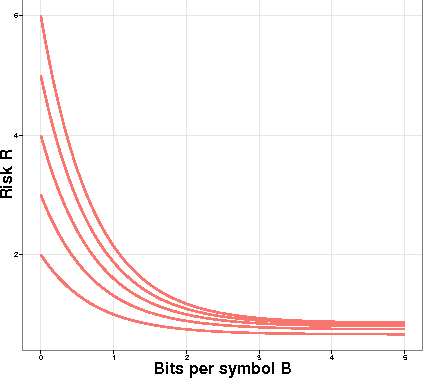
Abstract:A central result in statistical theory is Pinsker's theorem, which characterizes the minimax rate in the normal means model of nonparametric estimation. In this paper, we present an extension to Pinsker's theorem where estimation is carried out under storage or communication constraints. In particular, we place limits on the number of bits used to encode an estimator, and analyze the excess risk in terms of this constraint, the signal size, and the noise level. We give sharp upper and lower bounds for the case of a Euclidean ball, which establishes the Pareto-optimal minimax tradeoff between storage and risk in this setting.
Iterative Markov Chain Monte Carlo Computation of Reference Priors and Minimax Risk
Jan 10, 2013
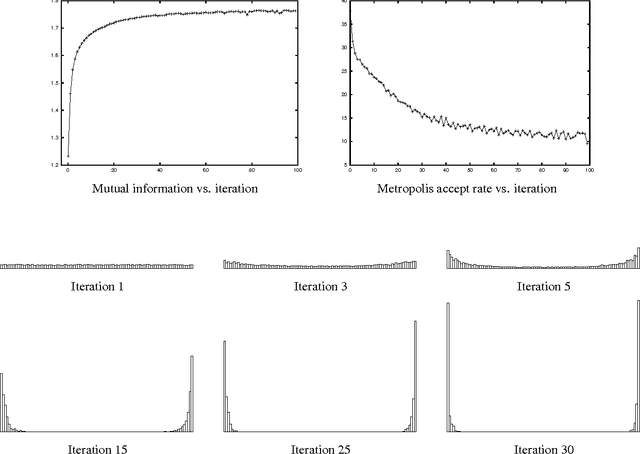
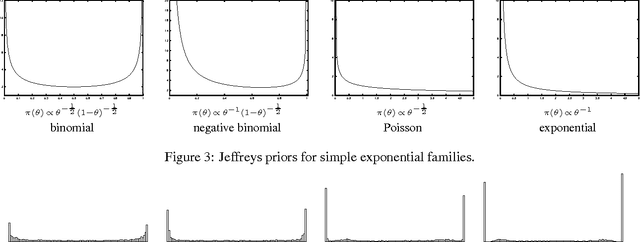
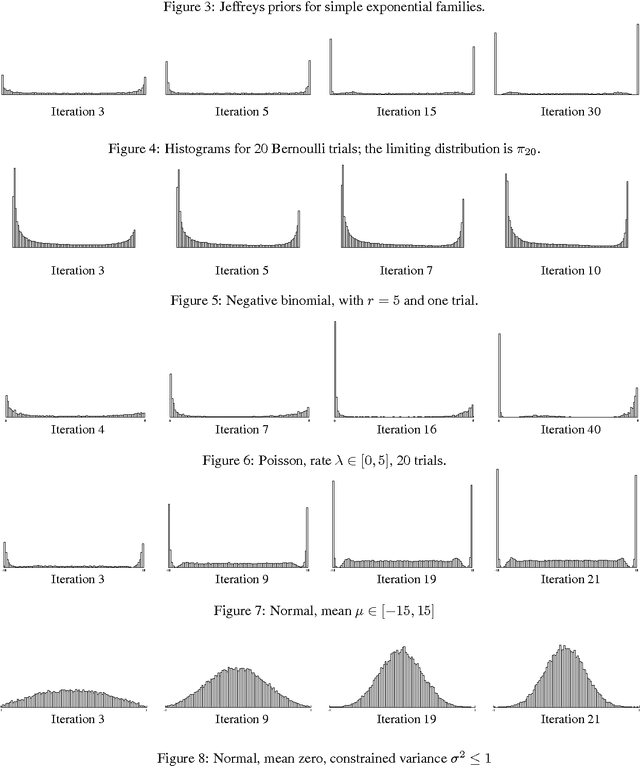
Abstract:We present an iterative Markov chainMonte Carlo algorithm for computingreference priors and minimax risk forgeneral parametric families. Ourapproach uses MCMC techniques based onthe Blahut-Arimoto algorithm forcomputing channel capacity ininformation theory. We give astatistical analysis of the algorithm,bounding the number of samples requiredfor the stochastic algorithm to closelyapproximate the deterministic algorithmin each iteration. Simulations arepresented for several examples fromexponential families. Although we focuson applications to reference priors andminimax risk, the methods and analysiswe develop are applicable to a muchbroader class of optimization problemsand iterative algorithms.
Nonparametric Reduced Rank Regression
Jan 09, 2013
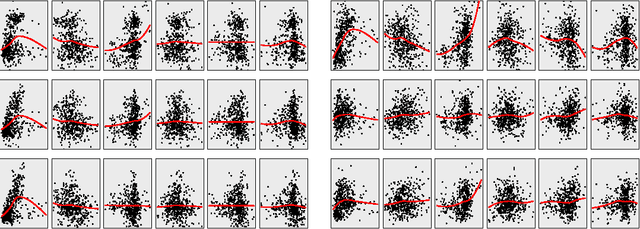
Abstract:We propose an approach to multivariate nonparametric regression that generalizes reduced rank regression for linear models. An additive model is estimated for each dimension of a $q$-dimensional response, with a shared $p$-dimensional predictor variable. To control the complexity of the model, we employ a functional form of the Ky-Fan or nuclear norm, resulting in a set of function estimates that have low rank. Backfitting algorithms are derived and justified using a nonparametric form of the nuclear norm subdifferential. Oracle inequalities on excess risk are derived that exhibit the scaling behavior of the procedure in the high dimensional setting. The methods are illustrated on gene expression data.
Sparse Nonparametric Graphical Models
Jan 07, 2013

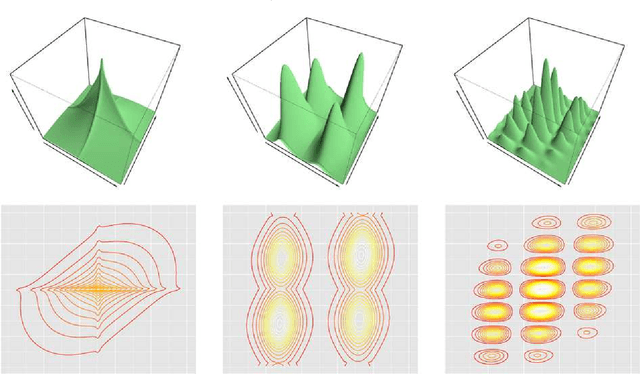

Abstract:We present some nonparametric methods for graphical modeling. In the discrete case, where the data are binary or drawn from a finite alphabet, Markov random fields are already essentially nonparametric, since the cliques can take only a finite number of values. Continuous data are different. The Gaussian graphical model is the standard parametric model for continuous data, but it makes distributional assumptions that are often unrealistic. We discuss two approaches to building more flexible graphical models. One allows arbitrary graphs and a nonparametric extension of the Gaussian; the other uses kernel density estimation and restricts the graphs to trees and forests. Examples of both methods are presented. We also discuss possible future research directions for nonparametric graphical modeling.
* Published in at http://dx.doi.org/10.1214/12-STS391 the Statistical Science (http://www.imstat.org/sts/) by the Institute of Mathematical Statistics (http://www.imstat.org)
Expectation-Propogation for the Generative Aspect Model
Dec 12, 2012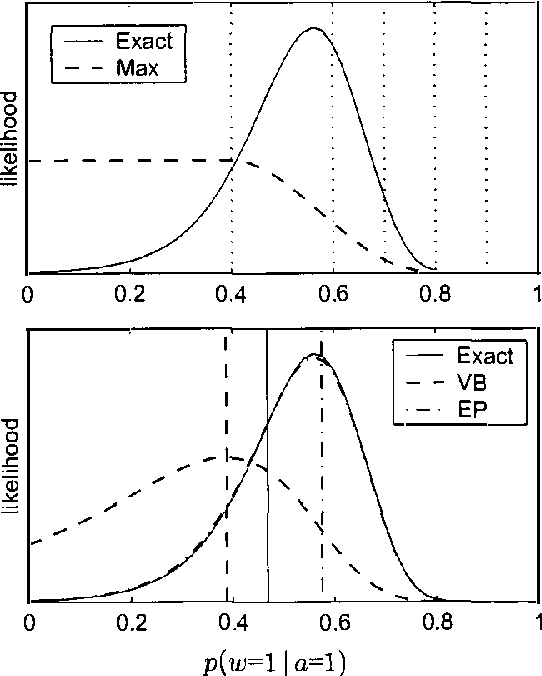

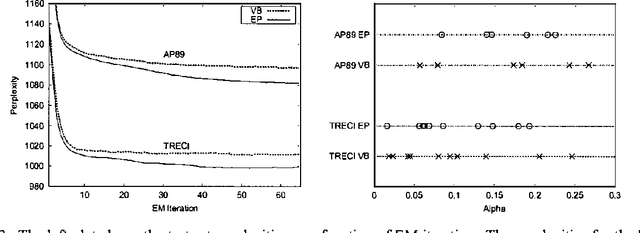
Abstract:The generative aspect model is an extension of the multinomial model for text that allows word probabilities to vary stochastically across documents. Previous results with aspect models have been promising, but hindered by the computational difficulty of carrying out inference and learning. This paper demonstrates that the simple variational methods of Blei et al (2001) can lead to inaccurate inferences and biased learning for the generative aspect model. We develop an alternative approach that leads to higher accuracy at comparable cost. An extension of Expectation-Propagation is used for inference and then embedded in an EM algorithm for learning. Experimental results are presented for both synthetic and real data sets.
High Dimensional Semiparametric Gaussian Copula Graphical Models
Jul 27, 2012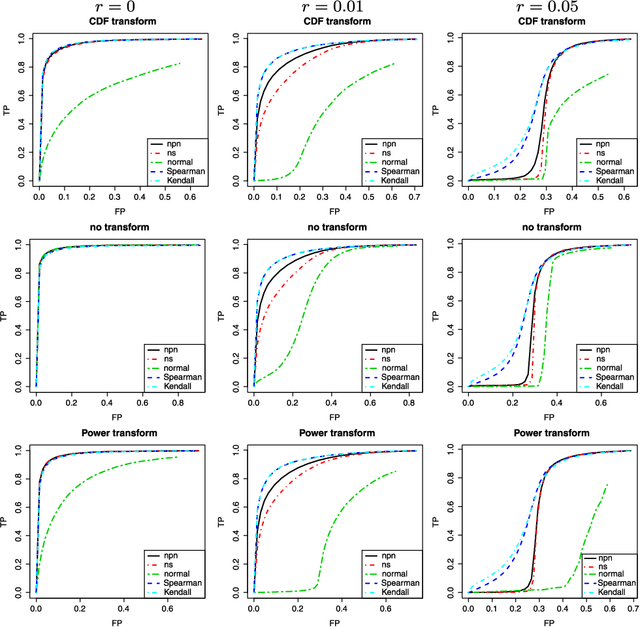
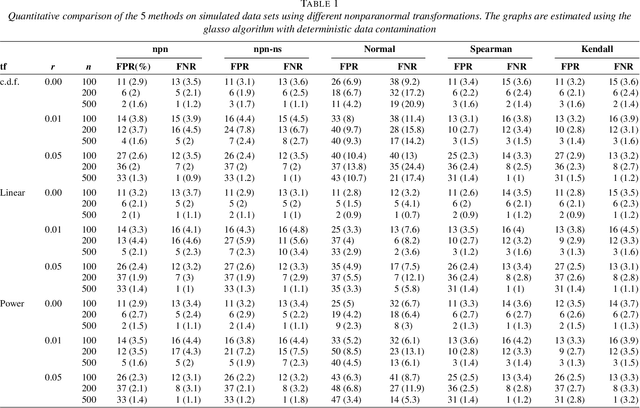
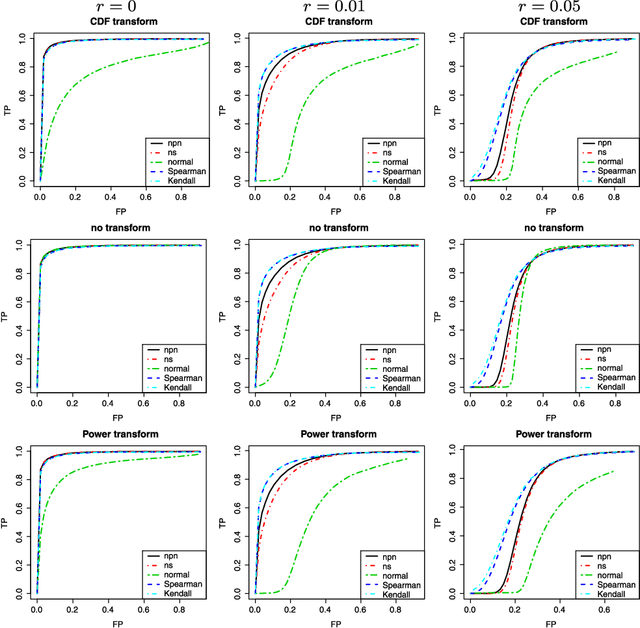
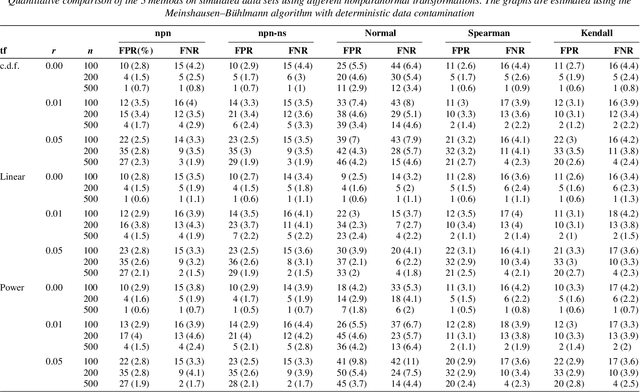
Abstract:In this paper, we propose a semiparametric approach, named nonparanormal skeptic, for efficiently and robustly estimating high dimensional undirected graphical models. To achieve modeling flexibility, we consider Gaussian Copula graphical models (or the nonparanormal) as proposed by Liu et al. (2009). To achieve estimation robustness, we exploit nonparametric rank-based correlation coefficient estimators, including Spearman's rho and Kendall's tau. In high dimensional settings, we prove that the nonparanormal skeptic achieves the optimal parametric rate of convergence in both graph and parameter estimation. This celebrating result suggests that the Gaussian copula graphical models can be used as a safe replacement of the popular Gaussian graphical models, even when the data are truly Gaussian. Besides theoretical analysis, we also conduct thorough numerical simulations to compare different estimators for their graph recovery performance under both ideal and noisy settings. The proposed methods are then applied on a large-scale genomic dataset to illustrate their empirical usefulness. The R language software package huge implementing the proposed methods is available on the Comprehensive R Archive Network: http://cran. r-project.org/.
Variational Chernoff Bounds for Graphical Models
Jul 11, 2012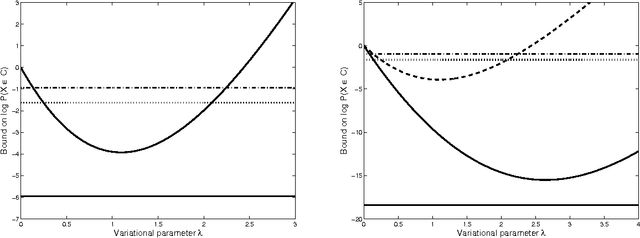
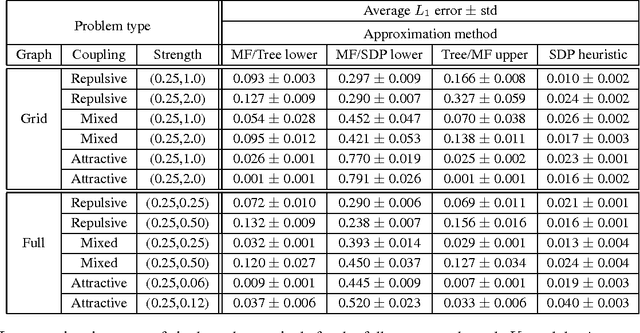
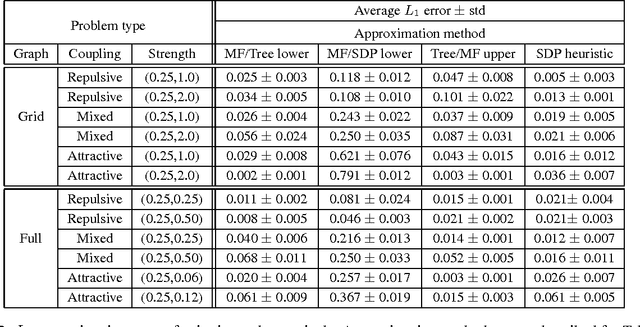
Abstract:Recent research has made significant progress on the problem of bounding log partition functions for exponential family graphical models. Such bounds have associated dual parameters that are often used as heuristic estimates of the marginal probabilities required in inference and learning. However these variational estimates do not give rigorous bounds on marginal probabilities, nor do they give estimates for probabilities of more general events than simple marginals. In this paper we build on this recent work by deriving rigorous upper and lower bounds on event probabilities for graphical models. Our approach is based on the use of generalized Chernoff bounds to express bounds on event probabilities in terms of convex optimization problems; these optimization problems, in turn, require estimates of generalized log partition functions. Simulations indicate that this technique can result in useful, rigorous bounds to complement the heuristic variational estimates, with comparable computational cost.
The Nonparanormal SKEPTIC
Jun 27, 2012



Abstract:We propose a semiparametric approach, named nonparanormal skeptic, for estimating high dimensional undirected graphical models. In terms of modeling, we consider the nonparanormal family proposed by Liu et al (2009). In terms of estimation, we exploit nonparametric rank-based correlation coefficient estimators including the Spearman's rho and Kendall's tau. In high dimensional settings, we prove that the nonparanormal skeptic achieves the optimal parametric rate of convergence in both graph and parameter estimation. This result suggests that the nonparanormal graphical models are a safe replacement of the Gaussian graphical models, even when the data are Gaussian.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge