Corrupted Sensing: Novel Guarantees for Separating Structured Signals

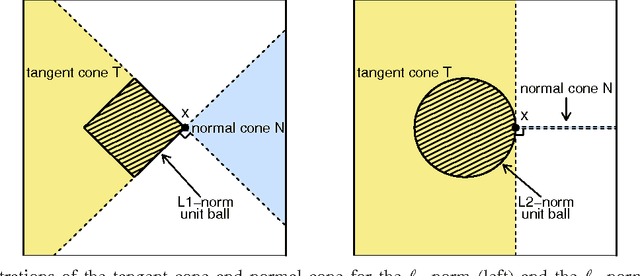
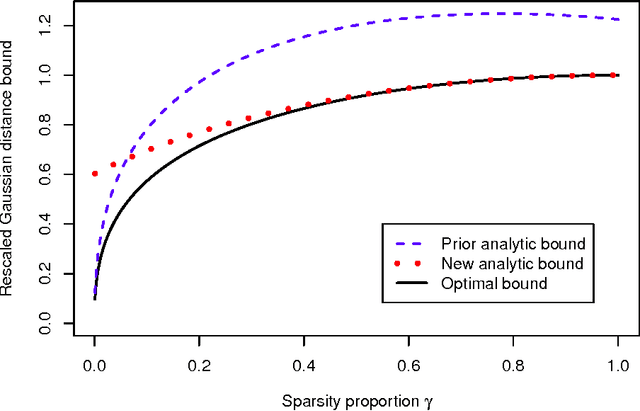
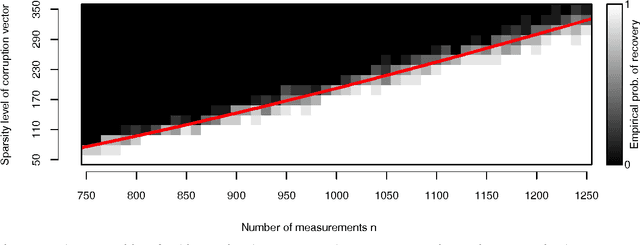
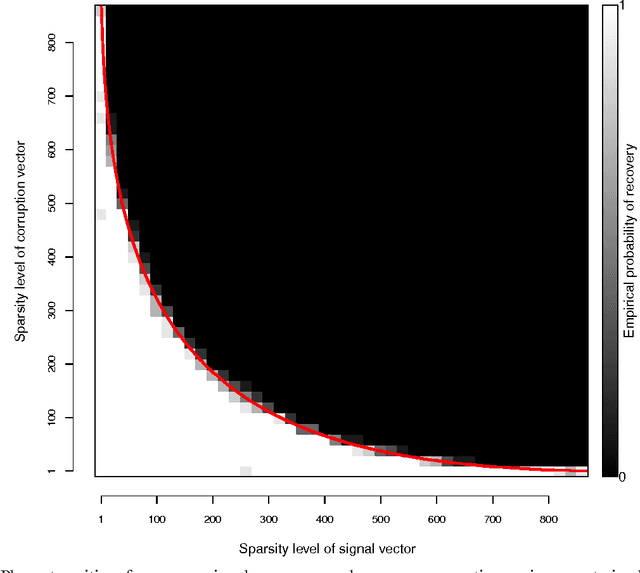
We study the problem of corrupted sensing, a generalization of compressed sensing in which one aims to recover a signal from a collection of corrupted or unreliable measurements. While an arbitrary signal cannot be recovered in the face of arbitrary corruption, tractable recovery is possible when both signal and corruption are suitably structured. We quantify the relationship between signal recovery and two geometric measures of structure, the Gaussian complexity of a tangent cone and the Gaussian distance to a subdifferential. We take a convex programming approach to disentangling signal and corruption, analyzing both penalized programs that trade off between signal and corruption complexity, and constrained programs that bound the complexity of signal or corruption when prior information is available. In each case, we provide conditions for exact signal recovery from structured corruption and stable signal recovery from structured corruption with added unstructured noise. Our simulations demonstrate close agreement between our theoretical recovery bounds and the sharp phase transitions observed in practice. In addition, we provide new interpretable bounds for the Gaussian complexity of sparse vectors, block-sparse vectors, and low-rank matrices, which lead to sharper guarantees of recovery when combined with our results and those in the literature.

Nonparametric Reduced Rank Regression

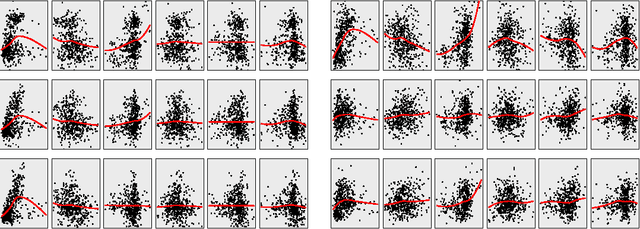
We propose an approach to multivariate nonparametric regression that generalizes reduced rank regression for linear models. An additive model is estimated for each dimension of a $q$-dimensional response, with a shared $p$-dimensional predictor variable. To control the complexity of the model, we employ a functional form of the Ky-Fan or nuclear norm, resulting in a set of function estimates that have low rank. Backfitting algorithms are derived and justified using a nonparametric form of the nuclear norm subdifferential. Oracle inequalities on excess risk are derived that exhibit the scaling behavior of the procedure in the high dimensional setting. The methods are illustrated on gene expression data.

Matrix reconstruction with the local max norm

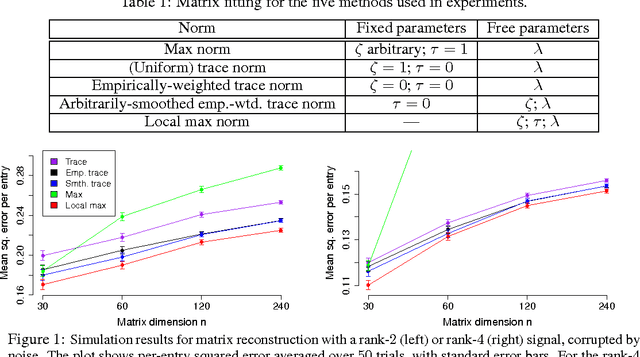
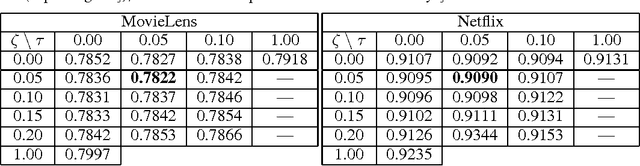
We introduce a new family of matrix norms, the "local max" norms, generalizing existing methods such as the max norm, the trace norm (nuclear norm), and the weighted or smoothed weighted trace norms, which have been extensively used in the literature as regularizers for matrix reconstruction problems. We show that this new family can be used to interpolate between the (weighted or unweighted) trace norm and the more conservative max norm. We test this interpolation on simulated data and on the large-scale Netflix and MovieLens ratings data, and find improved accuracy relative to the existing matrix norms. We also provide theoretical results showing learning guarantees for some of the new norms.

Sparse Prediction with the $k$-Support Norm

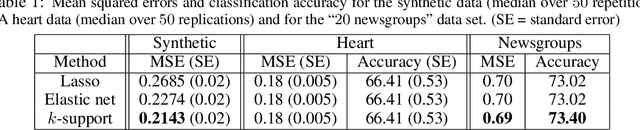
We derive a novel norm that corresponds to the tightest convex relaxation of sparsity combined with an $\ell_2$ penalty. We show that this new {\em $k$-support norm} provides a tighter relaxation than the elastic net and is thus a good replacement for the Lasso or the elastic net in sparse prediction problems. Through the study of the $k$-support norm, we also bound the looseness of the elastic net, thus shedding new light on it and providing justification for its use.

Learning with the Weighted Trace-norm under Arbitrary Sampling Distributions

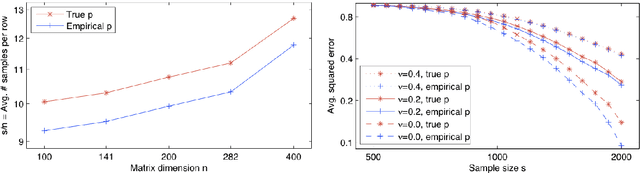
We provide rigorous guarantees on learning with the weighted trace-norm under arbitrary sampling distributions. We show that the standard weighted trace-norm might fail when the sampling distribution is not a product distribution (i.e. when row and column indexes are not selected independently), present a corrected variant for which we establish strong learning guarantees, and demonstrate that it works better in practice. We provide guarantees when weighting by either the true or empirical sampling distribution, and suggest that even if the true distribution is known (or is uniform), weighting by the empirical distribution may be beneficial.

Concentration-Based Guarantees for Low-Rank Matrix Reconstruction

We consider the problem of approximately reconstructing a partially-observed, approximately low-rank matrix. This problem has received much attention lately, mostly using the trace-norm as a surrogate to the rank. Here we study low-rank matrix reconstruction using both the trace-norm, as well as the less-studied max-norm, and present reconstruction guarantees based on existing analysis on the Rademacher complexity of the unit balls of these norms. We show how these are superior in several ways to recently published guarantees based on specialized analysis.

Exact block-wise optimization in group lasso and sparse group lasso for linear regression

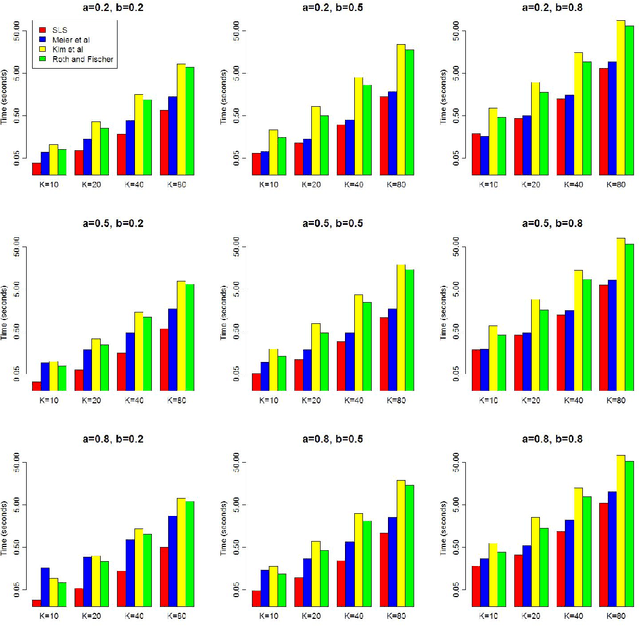
The group lasso is a penalized regression method, used in regression problems where the covariates are partitioned into groups to promote sparsity at the group level. Existing methods for finding the group lasso estimator either use gradient projection methods to update the entire coefficient vector simultaneously at each step, or update one group of coefficients at a time using an inexact line search to approximate the optimal value for the group of coefficients when all other groups' coefficients are fixed. We present a new method of computation for the group lasso in the linear regression case, the Single Line Search (SLS) algorithm, which operates by computing the exact optimal value for each group (when all other coefficients are fixed) with one univariate line search. We perform simulations demonstrating that the SLS algorithm is often more efficient than existing computational methods. We also extend the SLS algorithm to the sparse group lasso problem via the Signed Single Line Search (SSLS) algorithm, and give theoretical results to support both algorithms.