Johannes Maly
Conflicting Biases at the Edge of Stability: Norm versus Sharpness Regularization
May 27, 2025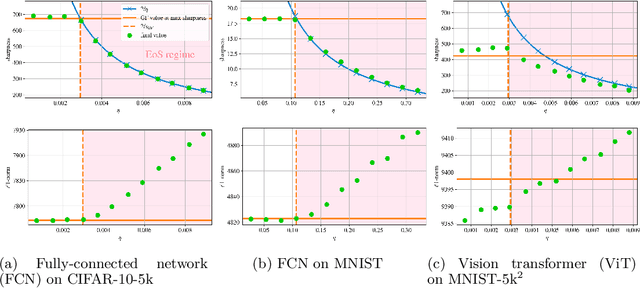
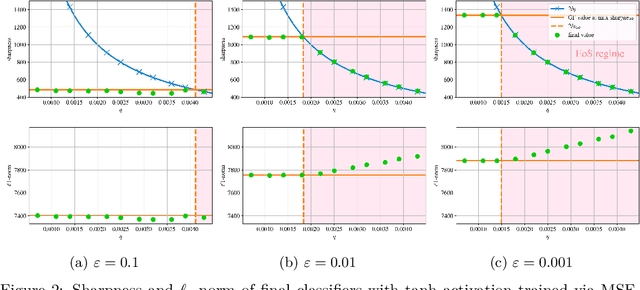
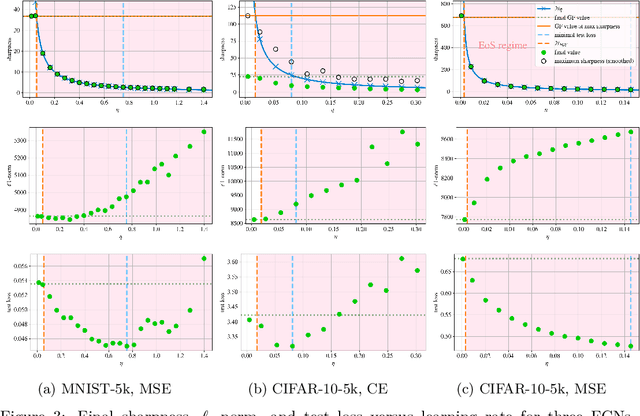
Abstract:A widely believed explanation for the remarkable generalization capacities of overparameterized neural networks is that the optimization algorithms used for training induce an implicit bias towards benign solutions. To grasp this theoretically, recent works examine gradient descent and its variants in simplified training settings, often assuming vanishing learning rates. These studies reveal various forms of implicit regularization, such as $\ell_1$-norm minimizing parameters in regression and max-margin solutions in classification. Concurrently, empirical findings show that moderate to large learning rates exceeding standard stability thresholds lead to faster, albeit oscillatory, convergence in the so-called Edge-of-Stability regime, and induce an implicit bias towards minima of low sharpness (norm of training loss Hessian). In this work, we argue that a comprehensive understanding of the generalization performance of gradient descent requires analyzing the interaction between these various forms of implicit regularization. We empirically demonstrate that the learning rate balances between low parameter norm and low sharpness of the trained model. We furthermore prove for diagonal linear networks trained on a simple regression task that neither implicit bias alone minimizes the generalization error. These findings demonstrate that focusing on a single implicit bias is insufficient to explain good generalization, and they motivate a broader view of implicit regularization that captures the dynamic trade-off between norm and sharpness induced by non-negligible learning rates.
Recovering Simultaneously Structured Data via Non-Convex Iteratively Reweighted Least Squares
Jun 08, 2023Abstract:We propose a new algorithm for the problem of recovering data that adheres to multiple, heterogeneous low-dimensional structures from linear observations. Focusing on data matrices that are simultaneously row-sparse and low-rank, we propose and analyze an iteratively reweighted least squares (IRLS) algorithm that is able to leverage both structures. In particular, it optimizes a combination of non-convex surrogates for row-sparsity and rank, a balancing of which is built into the algorithm. We prove locally quadratic convergence of the iterates to a simultaneously structured data matrix in a regime of minimal sample complexity (up to constants and a logarithmic factor), which is known to be impossible for a combination of convex surrogates. In experiments, we show that the IRLS method exhibits favorable empirical convergence, identifying simultaneously row-sparse and low-rank matrices from fewer measurements than state-of-the-art methods.
Plug-in Channel Estimation with Dithered Quantized Signals in Spatially Non-Stationary Massive MIMO Systems
Jan 11, 2023



Abstract:As the array dimension of massive MIMO systems increases to unprecedented levels, two problems occur. First, the spatial stationarity assumption along the antenna elements is no longer valid. Second, the large array size results in an unacceptably high power consumption if high-resolution analog-to-digital converters are used. To address these two challenges, we consider a Bussgang linear minimum mean square error (BLMMSE)-based channel estimator for large scale massive MIMO systems with one-bit quantizers and a spatially non-stationary channel. Whereas other works usually assume that the channel covariance is known at the base station, we consider a plug-in BLMMSE estimator that uses an estimate of the channel covariance and rigorously analyze the distortion produced by using an estimated, rather than the true, covariance. To cope with the spatial non-stationarity, we introduce dithering into the quantized signals and provide a theoretical error analysis. In addition, we propose an angular domain fitting procedure which is based on solving an instance of non-negative least squares. For the multi-user data transmission phase, we further propose a BLMMSE-based receiver to handle one-bit quantized data signals. Our numerical results show that the performance of the proposed BLMMSE channel estimator is very close to the oracle-aided scheme with ideal knowledge of the channel covariance matrix. The BLMMSE receiver outperforms the conventional maximum-ratio-combining and zero-forcing receivers in terms of the resulting ergodic sum rate.
A simple approach for quantizing neural networks
Sep 07, 2022Abstract:In this short note, we propose a new method for quantizing the weights of a fully trained neural network. A simple deterministic pre-processing step allows us to quantize network layers via memoryless scalar quantization while preserving the network performance on given training data. On one hand, the computational complexity of this pre-processing slightly exceeds that of state-of-the-art algorithms in the literature. On the other hand, our approach does not require any hyper-parameter tuning and, in contrast to previous methods, allows a plain analysis. We provide rigorous theoretical guarantees in the case of quantizing single network layers and show that the relative error decays with the number of parameters in the network if the training data behaves well, e.g., if it is sampled from suitable random distributions. The developed method also readily allows the quantization of deep networks by consecutive application to single layers.
More is Less: Inducing Sparsity via Overparameterization
Dec 21, 2021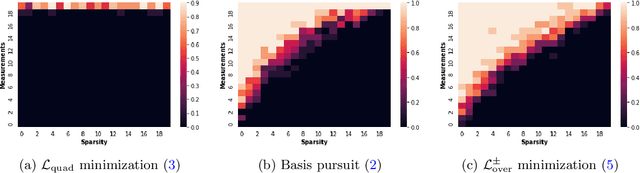
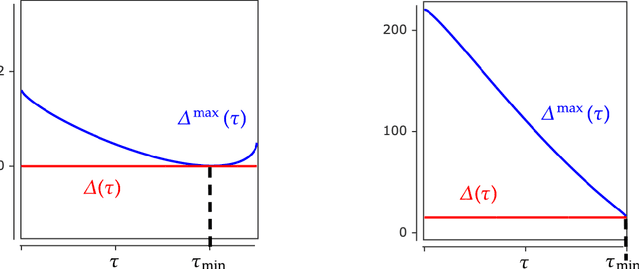
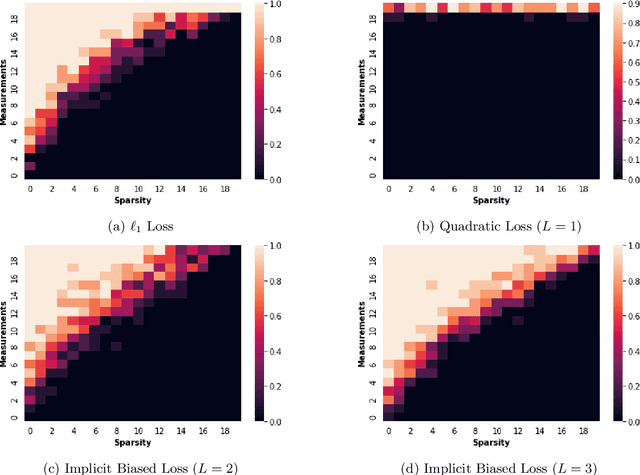
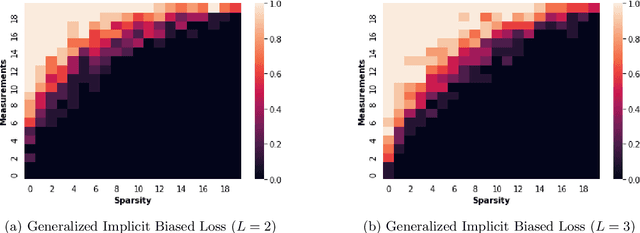
Abstract:In deep learning it is common to overparameterize the neural networks, that is, to use more parameters than training samples. Quite surprisingly training the neural network via (stochastic) gradient descent leads to models that generalize very well, while classical statistics would suggest overfitting. In order to gain understanding of this implicit bias phenomenon we study the special case of sparse recovery (compressive sensing) which is of interest on its own. More precisely, in order to reconstruct a vector from underdetermined linear measurements, we introduce a corresponding overparameterized square loss functional, where the vector to be reconstructed is deeply factorized into several vectors. We show that, under a very mild assumption on the measurement matrix, vanilla gradient flow for the overparameterized loss functional converges to a solution of minimal $\ell_1$-norm. The latter is well-known to promote sparse solutions. As a by-product, our results significantly improve the sample complexity for compressive sensing in previous works. The theory accurately predicts the recovery rate in numerical experiments. For the proofs, we introduce the concept of {\textit{solution entropy}}, which bypasses the obstacles caused by non-convexity and should be of independent interest.
Gradient Descent for Deep Matrix Factorization: Dynamics and Implicit Bias towards Low Rank
Nov 27, 2020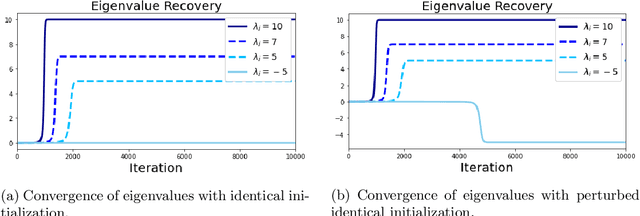
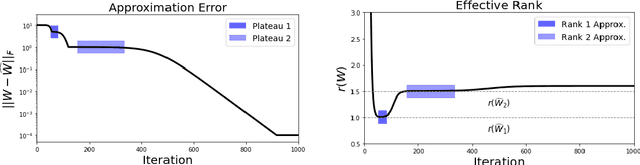
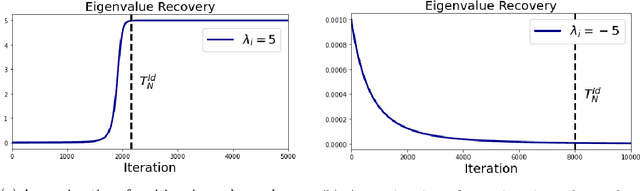
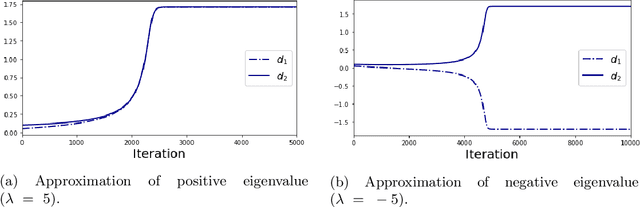
Abstract:We provide an explicit analysis of the dynamics of vanilla gradient descent for deep matrix factorization in a setting where the minimizer of the loss function is unique. We show that the recovery rate of ground-truth eigenvectors is proportional to the magnitude of the corresponding eigenvalues and that the differences among the rates are amplified as the depth of the factorization increases. For exactly characterized time intervals, the effective rank of gradient descent iterates is provably close to the effective rank of a low-rank projection of the ground-truth matrix, such that early stopping of gradient descent produces regularized solutions that may be used for denoising, for instance. In particular, apart from few initial steps of the iterations, the effective rank of our matrix is monotonically increasing, suggesting that "matrix factorization implicitly enforces gradient descent to take a route in which the effective rank is monotone". Since empirical observations in more general scenarios such as matrix sensing show a similar phenomenon, we believe that our theoretical results shed some light on the still mysterious "implicit bias" of gradient descent in deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge