Conflicting Biases at the Edge of Stability: Norm versus Sharpness Regularization

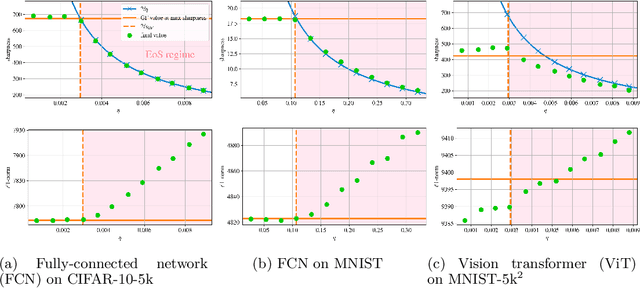
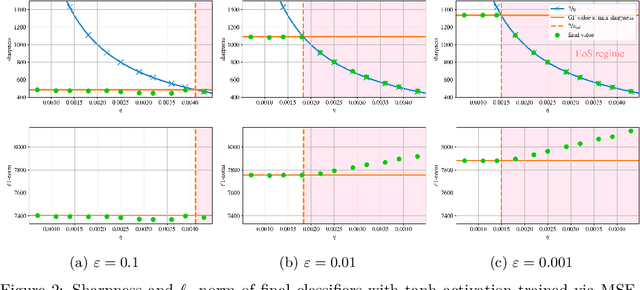
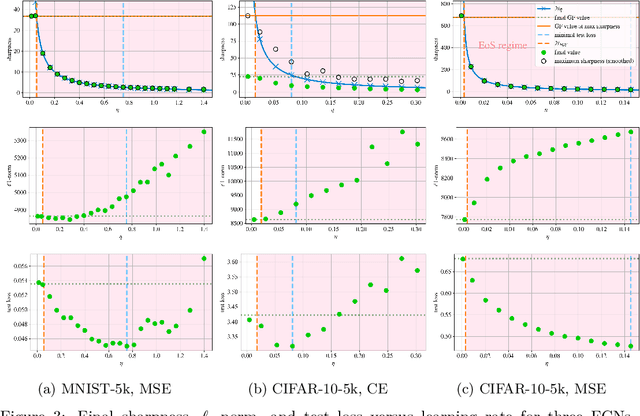
A widely believed explanation for the remarkable generalization capacities of overparameterized neural networks is that the optimization algorithms used for training induce an implicit bias towards benign solutions. To grasp this theoretically, recent works examine gradient descent and its variants in simplified training settings, often assuming vanishing learning rates. These studies reveal various forms of implicit regularization, such as $\ell_1$-norm minimizing parameters in regression and max-margin solutions in classification. Concurrently, empirical findings show that moderate to large learning rates exceeding standard stability thresholds lead to faster, albeit oscillatory, convergence in the so-called Edge-of-Stability regime, and induce an implicit bias towards minima of low sharpness (norm of training loss Hessian). In this work, we argue that a comprehensive understanding of the generalization performance of gradient descent requires analyzing the interaction between these various forms of implicit regularization. We empirically demonstrate that the learning rate balances between low parameter norm and low sharpness of the trained model. We furthermore prove for diagonal linear networks trained on a simple regression task that neither implicit bias alone minimizes the generalization error. These findings demonstrate that focusing on a single implicit bias is insufficient to explain good generalization, and they motivate a broader view of implicit regularization that captures the dynamic trade-off between norm and sharpness induced by non-negligible learning rates.

Computability of Classification and Deep Learning: From Theoretical Limits to Practical Feasibility through Quantization

The unwavering success of deep learning in the past decade led to the increasing prevalence of deep learning methods in various application fields. However, the downsides of deep learning, most prominently its lack of trustworthiness, may not be compatible with safety-critical or high-responsibility applications requiring stricter performance guarantees. Recently, several instances of deep learning applications have been shown to be subject to theoretical limitations of computability, undermining the feasibility of performance guarantees when employed on real-world computers. We extend the findings by studying computability in the deep learning framework from two perspectives: From an application viewpoint in the context of classification problems and a general limitation viewpoint in the context of training neural networks. In particular, we show restrictions on the algorithmic solvability of classification problems that also render the algorithmic detection of failure in computations in a general setting infeasible. Subsequently, we prove algorithmic limitations in training deep neural networks even in cases where the underlying problem is well-behaved. Finally, we end with a positive observation, showing that in quantized versions of classification and deep network training, computability restrictions do not arise or can be overcome to a certain degree.