Probabilistic and Differentiable Wireless Simulation with Geometric Transformers

Modelling the propagation of electromagnetic signals is critical for designing modern communication systems. While there are precise simulators based on ray tracing, they do not lend themselves to solving inverse problems or the integration in an automated design loop. We propose to address these challenges through differentiable neural surrogates that exploit the geometric aspects of the problem. We first introduce the Wireless Geometric Algebra Transformer (Wi-GATr), a generic backbone architecture for simulating wireless propagation in a 3D environment. It uses versatile representations based on geometric algebra and is equivariant with respect to E(3), the symmetry group of the underlying physics. Second, we study two algorithmic approaches to signal prediction and inverse problems based on differentiable predictive modelling and diffusion models. We show how these let us predict received power, localize receivers, and reconstruct the 3D environment from the received signal. Finally, we introduce two large, geometry-focused datasets of wireless signal propagation in indoor scenes. In experiments, we show that our geometry-forward approach achieves higher-fidelity predictions with less data than various baselines.

Simulating, Fast and Slow: Learning Policies for Black-Box Optimization

In recent years, solving optimization problems involving black-box simulators has become a point of focus for the machine learning community due to their ubiquity in science and engineering. The simulators describe a forward process $f_{\mathrm{sim}}: (\psi, x) \rightarrow y$ from simulation parameters $\psi$ and input data $x$ to observations $y$, and the goal of the optimization problem is to find parameters $\psi$ that minimize a desired loss function. Sophisticated optimization algorithms typically require gradient information regarding the forward process, $f_{\mathrm{sim}}$, with respect to the parameters $\psi$. However, obtaining gradients from black-box simulators can often be prohibitively expensive or, in some cases, impossible. Furthermore, in many applications, practitioners aim to solve a set of related problems. Thus, starting the optimization ``ab initio", i.e. from scratch, each time might be inefficient if the forward model is expensive to evaluate. To address those challenges, this paper introduces a novel method for solving classes of similar black-box optimization problems by learning an active learning policy that guides a differentiable surrogate's training and uses the surrogate's gradients to optimize the simulation parameters with gradient descent. After training the policy, downstream optimization of problems involving black-box simulators requires up to $\sim$90\% fewer expensive simulator calls compared to baselines such as local surrogate-based approaches, numerical optimization, and Bayesian methods.

End-to-end Learning of Deterministic Decision Trees

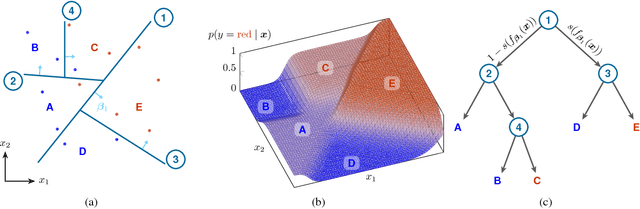
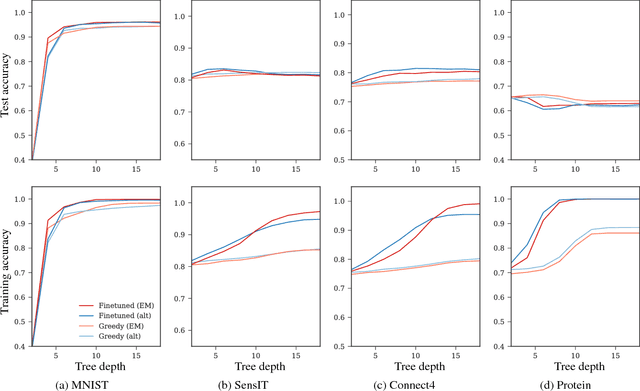
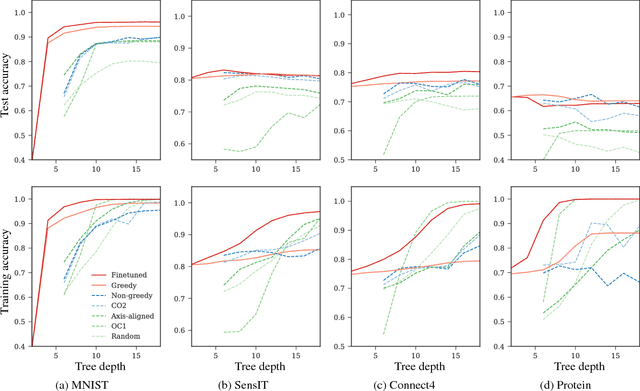
Conventional decision trees have a number of favorable properties, including interpretability, a small computational footprint and the ability to learn from little training data. However, they lack a key quality that has helped fuel the deep learning revolution: that of being end-to-end trainable, and to learn from scratch those features that best allow to solve a given supervised learning problem. Recent work (Kontschieder 2015) has addressed this deficit, but at the cost of losing a main attractive trait of decision trees: the fact that each sample is routed along a small subset of tree nodes only. We here propose a model and Expectation-Maximization training scheme for decision trees that are fully probabilistic at train time, but after a deterministic annealing process become deterministic at test time. We also analyze the learned oblique split parameters on image datasets and show that Neural Networks can be trained at each split node. In summary, we present the first end-to-end learning scheme for deterministic decision trees and present results on par with or superior to published standard oblique decision tree algorithms.